数据降维3：降维映射及PCA的实现与使用

数据降维第三弹来啦！

0x01 高维数据向低维数据映射

在之前已经学习了如何求一个数据集的前n个主成分，但是数据集本身已经是n维的，并没有进行降维度。那么PCA是如何降维的呢？如何从高维数据向低维数据映射？

主成分分析的作用就是选出能使样本方差最大的维度，选择完维度之后，进入对数据降维的操作。将高维数据映射为低维数据。

假设经过主成分分析之后，左侧 还是数据样本，一个 的矩阵，m个样本n个特征。根据主成分分析法求出了前k个主成分，得到 矩阵，即有k个主成分向量，每个主成分的坐标系有n个维度（与转换前的维度相同），形成一个 的矩阵。

如何将样本X从n维转换为k维呢？

对于一个样本 来说，分别点乘 中的每一行（），得到k个数，这k个数组成的向量。即表示将样本 映射到了 这个坐标向量上，得到的新的k维向量，即完成了高维n到低维k的映射。对于每个样本，依次类推，就将所有样本从n维映射到k维。其实就相当于做一个矩阵乘法，得到一个 的矩阵（注意，这里需要转置）：

在这个降维的过程中可能会丢失信息。如果原先的数据中本身存在一些无用信息，降维也可能会有降噪效果。

0x02 PCA代码实现

• 定义一个类PCA，构造函数函数中n_components表示主成分个数即降维后的维数，components_表示主成分  ；

• 函数fit()与上面的first_n_component()方法一样，用于求出 ；

• 函数transform()将 映射到各个主成分分量中，得到 ，即降维；

• 函数transform()将 映射到原来的特征空间，得到 。

import numpy as np




class PCA:
    def __init__(self, n_components):
        # 主成分的个数n
        self.n_components = n_components
        # 具体主成分
        self.components_ = None


    def fit(self, X, eta=0.001, n_iters=1e4):
        '''均值归零'''
        def demean(X):
            return X - np.mean(X, axis=0)


        '''方差函数'''
        def f(w, X):
            return np.sum(X.dot(w) ** 2) / len(X)
        
        '''方差函数导数'''
        def df(w, X):
            return X.T.dot(X.dot(w)) * 2 / len(X)


        '''将向量化简为单位向量'''
        def direction(w):
            return w / np.linalg.norm(w)


        '''寻找第一主成分'''
        def first_component(X, initial_w, eta, n_iters, epsilon=1e-8):
            w = direction(initial_w)
            cur_iter = 0
            while cur_iter < n_iters:
                gradient = df(w, X)
                last_w = w
                w = w + eta * gradient
                w = direction(w) 
                if(abs(f(w, X) - f(last_w, X)) < epsilon):
                    break      
                cur_iter += 1     
            return w
        
        # 过程如下：
        # 归0操作
        X_pca = demean(X)
        # 初始化空矩阵，行为n个主成分，列为样本列数
        self.components_ = np.empty(shape=(self.n_components, X.shape[1]))
        # 循环执行每一个主成分
        for i in range(self.n_components):
            # 每一次初始化一个方向向量w
            initial_w = np.random.random(X_pca.shape[1])
            # 使用梯度上升法，得到此时的X_PCA所对应的第一主成分w
            w = first_component(X_pca, initial_w, eta, n_iters)
            # 存储起来
            self.components_[i:] = w
            # X_pca减去样本在w上的所有分量，形成一个新的X_pca，以便进行下一次循环
            X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
        
        return self


    # 将X数据集映射到各个主成分分量中
    def transform(self, X):
        assert X.shape[1] == self.components_.shape[1]
        return X.dot(self.components_.T)


    def inverse_transform(self, X):
        return X.dot(self.components_)

0x03 sklearn中的PCA

3.1 PCA的使用

如何使用sklearn中的PCA呢？首先准备数据：

import numpy as np
import matplotlib.pyplot as plt


X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)

然后fit一下，求出主成分

from sklearn.decomposition import PCA


# 初始化实例对象，传入主成分个数
pca = PCA(n_components=1)
pca.fit(X)

验证一下pca求出的主成分，是一个方向向量：

pca.components_
# 输出
array([[-0.76676934, -0.64192272]])

在得到主成分之后，使用transform方法将矩阵X进行降维。得到一个特征的数据集。

X_reduction = pca.transform(X)
X_reduction.shape
# 输出
(100,1)

3.2 真实数据降维

为了验证PCA算法在真实数据中的威力，我们对手写数据集digits使用主成分分析法进行降维，再用kNN算法进行分类，观察前后的结果有何不同。

首先准备数据集：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier


digits = datasets.load_digits()
X = digits.data
y = digits.target


X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

对原始数据集进行训练，看看识别的结果

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)
knn_clf.score(X_test, y_test)
# 输出：
0.98666666666666669

下面用PCA算法对数据进行降维：

from sklearn.decomposition import PCA


pca = PCA(n_components=2)
pca.fit(X_train)
X_train_reduction = pca.transform(X_train) # 训练数据集降维结果
X_test_reduction = pca.transform(X_test) # 测试数据集降维结果

下面使用降维后的数据，观察其kNN算法的识别精度：

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test)
# 输出：
0.60666666666666669

可以看到，数据由64维降到2维之后，精度也相应的降低了。那么我们具体应该降低到哪维呢？n_components参数如何设置？

3.3 主成分解释方差比例

PCA算法提供了一个特殊的指标pca.explained_variance_ratio_（解释方差比例），我们可以使用这个指标找到某个数据集保持多少的精度：

pca.explained_variance_ratio_
# 输出：
array([ 0.14566817,  0.13735469])

上面就是主成分所解释的方差比例。对于现在的PCA算法来说，得到的是二维数据：0.14566817表示第一个轴能够解释14.56%数据的方差；0.13735469表示第二个轴能够解释13.73%数据的方差。PCA过程寻找主成分，就是找使得原数据的方差维持的最大。这个值就告诉我们，PCA最大维持了原来所有方差的百分比。对于这两个维度来说，[ 0.14566817, 0.13735469]涵盖了原数据的总方差的28%左右的信息，剩下72%的方差信息就丢失了，显然丢失的信息过多。

下面我们使用PCA算法保持数据64维：

pca = PCA(n_components=X_train.shape[1])
pca.fit(X_train)
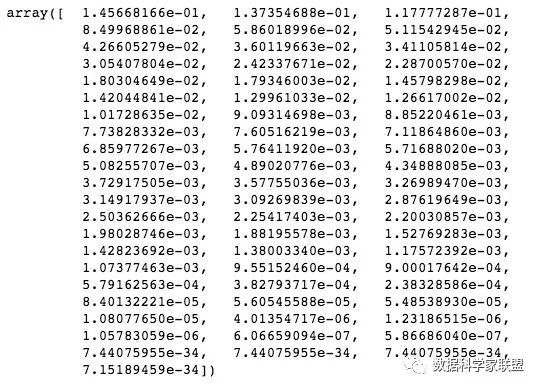
pca.explained_variance_ratio_

训练数据集是一个含有64个特征的数据集，经过主成分分析得到的explained_variance_ratio_也是一个含有64个元素的数据集，表示每个主成分对原始数据方差的解释度。从结果可以看出，所占方差的比例是一个从大到小的排列。第一个轴占了14.56%，最后几个的解释度几乎为零，也就是说对原始方差基本没有作用,完全可以忽略不计。也就是说可以将主成分所解释的方差比例视为重要程度。

这种方式虽然耗时增加了，但分类的准确度提高了。在实际情况下，可能会忽略对原始方差影响小的成分，在时间和准确度之间做一个权衡。因此我们可以绘制下面的折线图：

# 横轴是是样本X的i个特征数，纵轴是前i个轴解释方差比例的和
plt.plot([i for i in range(X_train.shape[1])], 
         [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()

如果我们希望保持95%以上的信息，就能得到相应的降维后的主成分个数。在sklearn中，实例化时传入一个数字，就表示保持的方差比例：

pca = PCA(0.95)
pca.fit(X_train)
# 输出：
PCA(copy=True, iterated_power='auto', n_components=0.95, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False)

查看一下降维后主成分的个数为28，即对于64维数据来说，28维数据就可以解释95%以上的方差。

pca.n_components_
# 输出：
28

然后用这种pca去重新使用kNN做训练，得到的结果较好。

X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test)
# 输出
0.97999999999999998

数据降维还有一个作用是可视化，降到2维数据之后：

pca = PCA(n_components=2)
pca.fit(X)
X_reduction = pca.transform(X)
for i in range(10):
    plt.scatter(X_reduction[y==i,0], X_reduction[y==i,1], alpha=0.8)
plt.show()

0xFF 总结

我们已经知道了，PCA法是通过选出使样本方差最大的维度来求主成分的。那么确定了主成分的方向向量后，就需要将高维数据向低维数据映射。方法就是将样本分别点乘每一个主成分向量（数），得到k个数并组成向量。以此类推，完成高维n到低维k的映射。其公式为：

我们在使用sklearn中提高的PCA方法时，需要先初始化实例对象（此时可以传递主成分个数），fit操作得到主成分后进行降维映射操作pca.transform。在初始化实例对象时，也可以传入一个数字，表示主成分所解释的方差比例，即每个主成分对原始数据方差的重要程度。忽略对原始方差影响小的成分，在时间和准确度之间做一个权衡。

下一篇文章会介绍一些主成分分析法的小应用，大家加油～