2020 Multi-University Training Contest 3
施工中。。。
1004 Tokitsukaze and Multiple
题目要求最多字段,使其和为p的倍数。很显然可以用dp解决,\(dp[i]=max(dp[i-1],dp[k]+1),sum[k]\%p==sum[i]\%p\),只要记录模p同余的上一个位置即可。
#include
#define ll long long
#define maxn 100010
#define mod 998244353
using namespace std;
int a[maxn], sum[maxn], dp[maxn], las[maxn];
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n, p;
scanf("%d%d", &n, &p);
int ans = 0;
for (int i = 0; i <= p; i++) las[i] = 0;
for (int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
x %= p;
a[i] = x;
}
for (int i = 1; i <= n; i++) sum[i] = (sum[i - 1] + a[i]) % p;
for (int i = 1; i <= n; i++) {
dp[i] = dp[i - 1];
if (las[sum[i]] == 0 && sum[i] != 0) dp[i] = max(dp[i], dp[las[sum[i]]]);
else dp[i] = max(dp[i], dp[las[sum[i]]] + 1);
las[sum[i]] = i;
ans = max(ans, dp[i]);
}
printf("%d\n", ans);
}
return 0;
}
1005 Little W and Contest
这题看上去就很排列组合,实际上使用带权并查集和简单组合数就可以解决。
计算原先有的组合数量,然后记录每个分块中两种学生的数量。将分块合并时要减去其中损失的组合数,然后权值合并。
#include
#define ll long long
#define maxn 100010
#define mod 1000000007
using namespace std;
ll f[maxn], s1[maxn], s2[maxn];
int fi(int x) {
if (f[x] == x) return x;
f[x] = fi(f[x]);
return f[x];
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n;
scanf("%d", &n);
ll sum1 = 0, sum2 = 0;
for (int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
f[i] = i, s1[i] = s2[i] = 0;
if (x == 1) s1[i]++, sum1++;
else s2[i]++, sum2++;
}
ll ans = 0;
ans = sum1 * (sum2 * (sum2 - 1) / 2) % mod % mod + (sum2 * (sum2 - 1) / 2 * (sum2 - 2) / 3) % mod;
ans %= mod;
vectorv;
v.push_back(ans);
for (int i = 1; i < n; i++) {
int x, y;
scanf("%d%d", &x, &y);
x = fi(x), y = fi(y);
ans -= (sum1 - s1[x] - s1[y]) * s2[x] % mod * s2[y] % mod;
ans %= mod;
ans -= (sum2 - s2[x] - s2[y]) * s1[x] % mod * s2[y] % mod;
ans %= mod;
ans -= (sum2 - s2[x] - s2[y]) * s2[x] % mod * s1[y] % mod;
ans %= mod;
ans -= (sum2 - s2[x] - s2[y]) * s2[x] % mod * s2[y] % mod;
ans %= mod;
while (ans < 0) ans += mod;
s1[x] += s1[y];
s2[x] += s2[y];
f[y] = x;
v.push_back(ans);
}
for (int i = 0; i < v.size(); i++) printf("%lld\n", v[i]);
}
return 0;
}
1006 X Number
\(dp[pos][cnt][num]\) \(pos\) 为剩余的位数、\(cnt\) 为前面位数的组合情况、\(num\) 为要搜索的数的个数
本题要查询 \(0-9\) 每一位的位数,我们将 \(19\) 位分成若干个 \(0-9\) ,如\(\{(13,0),(2,1),(2,3),(1,4),(1,5),(0,6),(0,7),(0,8),(0,9)\}\),大概有几千万种情况
事实上 \(0-9\) 对于我们来说只有等于 \(d\) 和不等于 \(d\) 的区别,那么仅把 \(19\) 个数分成若干块,如 \(\{13,2,2,1,1,0,0,0,0,0\}\),只有约 \(2000\) 种情况
那么我们用 map 来存储划分的情况,既可以在复杂度允许的情况,来表示划分。
接下来,用 \(num\) 表示要搜索的数的个数,唯一标识划分的情况
最后,数位 \(dp\) 暴力转移即可
#include
using namespace std;
typedef long long LL;
const int maxn = 2005;
const int base = 25;
int Case = 0;
int g;
vector tmp, E[maxn];
map, int> Map;
void init(int now, int k) {
if (now == 10) {
Map[tmp] = ++g;
E[g] = tmp;
return;
}
int top = k;
if (now)
top = min(top, tmp[now - 1]);
for (int i = 0; i <= top; i++) {
tmp.push_back(i);
init(now + 1, k - i);
tmp.pop_back();
}
}
int a[base], len, d;
LL dp[base][maxn][base];
int limit_v[15], limit_cnt[base];
vector limit_vc[base];
LL dfs(int pos, int cnt, int num, bool lead, bool limit) {
if (pos > len) {
if (E[cnt][0] > E[cnt][1] && E[cnt][0] == num) {
return 1;
} else
return 0;
}
if (dp[len - pos + 1][cnt][num] != -1 && (!lead) && (!limit))
return dp[len - pos + 1][cnt][num];
LL res = 0;
int top = limit ? a[len - pos + 1] : 9;
if (lead) {
res += dfs(pos + 1, cnt, num, lead, false);
int top3 = top;
if (limit)
top3--;
for (int i = 1; i <= top3; i++) {
vector tmp(10, 0);
tmp[0] = 1;
res += dfs(pos + 1, Map[tmp], num + (d == i), false, false);
}
if (limit)
res += dfs(pos + 1, limit_cnt[pos], num + (d == top), false, true);
} else if (limit) {
vector vc(10, 0);
for (int i = 1; i < pos; i++)
vc[a[len - i + 1]]++;
for (int i = 0; i < top; i++) {
vector temp = vc;
temp[i]++;
sort(temp.begin(), temp.end(), [](const int a, const int b) {
return a > b;
});
res += dfs(pos + 1, Map[temp], num + (d == i), false, false);
}
res += dfs(pos + 1, limit_cnt[pos], num + (d == top), false, true);
} else {
bool check = true;
int add = 0;
for (int i = 0; i < 10; i++) {
vector temp = E[cnt];
if (check && temp[i] == num) {
check = false;
add = 1;
} else
add = 0;
temp[i]++;
sort(temp.begin(), temp.end(), [](const int a, const int b) {
return a > b;
});
res += dfs(pos + 1, Map[temp], num + add, false, false);
}
}
if ((!lead) && (!limit))
dp[len - pos + 1][cnt][num] = res;
return res;
}
LL doit(LL x) {
len = 0;
memset(a, 0, sizeof(a));
while (x) {
a[++len] = x % 10;
x /= 10;
}
memset(limit_v, 0, sizeof(limit_v));
for (int i = 1; i <= len; i++) {
limit_v[a[len - i + 1]]++;
limit_vc[i].clear();
for (int j = 0; j <= 9; j++)
limit_vc[i].push_back(limit_v[j]);
sort(limit_vc[i].begin(), limit_vc[i].end(), [](const int a, const int b) {
return a > b;
});
limit_cnt[i] = Map[limit_vc[i]];
}
return dfs(1, 1, 0, true, true);
}
int main() {
init(0, 19);
memset(dp, -1, sizeof(dp));
int t;
scanf("%d", &t);
while (t--) {
Case++;
LL left, right;
scanf("%lld%lld", &left, &right);
scanf("%d", &d);
printf("%lld\n", doit(right) - doit(left - 1));
}
return 0;
}
1007 Tokitsukaze and Rescue
由于题目数量是随机的,所以最短路的长度不会很长。那么每次暴力删除最短路中的一段路径,记录删除k条路后能得到的最大值即可。
#include
#define ll long long
#define maxn 100010
#define mod 1000000007
using namespace std;
int n, k;
int mp[60][60];
int ans;
struct cv {
int x, y;
friend bool operator<(cv p, cv q) {
return p.y > q.y;
}
}dd, bb;
int las[60], len[60];
void sol(int x) {
for (int i = 1; i <= n; i++) {
las[i] = 0, len[i] = 1e8;
}
len[1] = 0;
dd.x = 1, dd.y = 0;
priority_queueq;
q.push(dd);
while (!q.empty()) {
dd = q.top();
q.pop();
if (dd.x == n) break;
if (dd.y != len[dd.x]) continue;
for (int i = 1; i <= n; i++) {
if (i == dd.x) continue;
if (dd.y + mp[dd.x][i] < len[i]) {
las[i] = dd.x;
len[i] = dd.y + mp[dd.x][i];
bb.x = i, bb.y = len[i];
q.push(bb);
}
}
}
if (x == k) {
ans = max(ans, len[n]);
return;
}
int tp = n;
vectorv;
while (tp != 0) {
v.push_back(tp);
tp = las[tp];
}
for (int i = 0; i < v.size() - 1; i++) {
int t1 = v[i], t3 = v[i + 1];
int y = mp[t1][t3];
mp[t1][t3] = mp[t3][t1] = 1e8;
sol(x + 1);
mp[t1][t3] = mp[t3][t1] = y;
}
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
scanf("%d%d", &n, &k);
for (int i = 0; i < n * (n - 1) / 2; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
mp[x][y] = mp[y][x] = z;
}
ans = 0;
sol(0);
printf("%d\n", ans);
}
return 0;
}
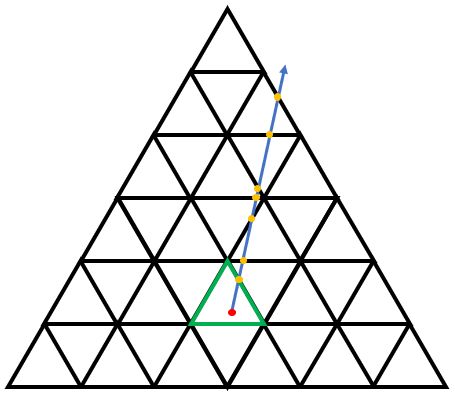
1008 Triangle Collision
二分时间。将正三角形展开,铺满整个平面,正三角形内的反射可以看作射线与展开后的正三角形平面的所有交点(如下图)。我们发现一共只有三种平行的直线,只要分别求出这条射线和这三种直线的交点分布就能 \(O(1)\) \(\text{check}\) 了。
#include
#define db double
using namespace std;
const db eps = 1e-5;
const db pi = acos(-1.0);
int sign(db k) {
if (k > eps) return 1;
else if (k < -eps) return -1;
return 0;
}
int cmp(db k1, db k2) { return sign(k1 - k2); }
struct point {
db x, y;
point() {}
point(db x_, db y_) :x(x_), y(y_) {}
point operator + (const point& k) const { return point(k.x + x, k.y + y); }
point operator - (const point& k) const { return point(x - k.x, y - k.y); }
point operator * (db k) const { return point(x * k, y * k); }
point operator / (db k1) const { return point(x / k1, y / k1); }
point turn(db k1) { return point(x * cos(k1) - y * sin(k1), x * sin(k1) + y * cos(k1)); } // 逆时针旋转
point turn90() { return point(-y, x); } // 逆时针方向旋转 90 度
db len() { return sqrt(x * x + y * y); } // 向量长度
db len2() { return x * x + y * y; } // 向量长度
db dis(point rhs) { return ((*this) - rhs).len(); }
point unit() { db d = len(); return point(x / d, y / d); }
bool operator < (const point& k) const {
return x == k.x ? y < k.y : x < k.x;
}
bool getP() const { return sign(y) == 1 || (sign(y) == 0 && sign(x) == -1); }
}triangleVertex[3];
db cross(point k1, point k2) { return k1.x * k2.y - k1.y * k2.x; }
db dot(point k1, point k2) { return k1.x * k2.x + k1.y * k2.y; }
db rad(point k1, point k2) { return atan2(cross(k1, k2), dot(k1, k2)); }
int compareangle(point k1, point k2) {
return k1.getP() < k2.getP() || (k1.getP() == k2.getP() && sign(cross(k1, k2)) > 0);
}
point proj(point k1, point k2, point q) { // q 到直线 k1,k2 的投影
point k = k2 - k1; return k1 + k * (dot(q - k1, k) / k.len2());
}
point reflect(point k1, point k2, point q) { return proj(k1, k2, q) * 2 - q; } // q 关于直线 k1,k2 的对称点
int clockwise(point k1, point k2, point k3) { // k1 k2 k3 逆时针1 顺时针-1 否则0
return sign(cross(k2 - k1, k3 - k1));
}
int checkLL(point k1, point k2, point k3, point k4) { // 求直线(L) 线段(S) k1,k2 和 k3,k4 的交点
return cmp(cross(k3 - k1, k4 - k1), cross(k3 - k2, k4 - k2)) != 0;
}
struct line {
point p[2];
line() {}
line(point k1, point k2) { p[0] = k1, p[1] = k2; }
point& operator [] (int k) { return p[k]; }
point dir() { return p[1] - p[0]; }
bool include(point k) { return sign(cross(p[1] - p[0], k - p[0])) > 0; }
line push(db len) { // 向外(左手边)平移 len 个单位
point delta = (p[1] - p[0]).turn90().unit() * len;
return line(p[0] - delta, p[1] - delta);
}
}triangle[3];
bool parallel(line k1, line k2) { return sign(cross(k1.dir(), k2.dir())) == 0; }
bool sameDir(line k1, line k2) { return parallel(k1, k2) && sign(dot(k1.dir(), k2.dir())) == 1; }
bool operator < (line k1, line k2) {
if (sameDir(k1, k2)) return k2.include(k1[0]);
return compareangle(k1.dir(), k2.dir());
}
point getLL(point k1, point k2, point k3, point k4) { // 两直线交点
db w1 = cross(k1 - k3, k4 - k3), w2 = cross(k4 - k3, k2 - k3);
return (k1 * w2 + k2 * w1) / (w1 + w2);
}
point getLL(line k1, line k2) { return getLL(k1[0], k1[1], k2[0], k2[1]); }
bool checkpos(line k1, line k2, line k3) { return k3.include(getLL(k1, k2)); }
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
int t; cin >> t;
while (t--) {
db len, x, y, vx, vy = 0.0;
db L = 0.0, R = 1e20, mid;
long long k;
vector initTime(3); // 第一次交直线的时间
vector crossTime(3); // 两次相交的间隔时间
vector vis(3, false);
cin >> len >> x >> y >> vx >> vy >> k;
triangleVertex[0] = point(0.5 * len, 0);
triangleVertex[1] = point(-0.5 * len, 0);
triangleVertex[2] = point(0, 0.5 * sqrt(3.0) * len);
triangle[0] = line(triangleVertex[0], triangleVertex[1]);
triangle[1] = line(triangleVertex[1], triangleVertex[2]);
triangle[2] = line(triangleVertex[2], triangleVertex[0]);
point now = point(x, y);
point dir = point(vx, vy) + now;
line vec = line(now, dir);
for (int i = 0; i < 3; ++i) {
if (parallel(vec, triangle[i])) {
vis[i] = true;
continue;
}
point intersection = getLL(vec, triangle[i]);
if (!sameDir(line(now, intersection), vec)) {
triangle[i] = triangle[i].push(0.5 * sqrt(3.0) * len);
intersection = getLL(vec, triangle[i]);
}
initTime[i] = now.dis(intersection);
line nxtL = triangle[i].push(0.5 * sqrt(3.0) * len);
point nxt = getLL(vec, nxtL);
crossTime[i] = intersection.dis(nxt);
}
auto cal = [&](int i, db time) {
if (vis[i]) return 0ll;
long long cnt = 0;
if (cmp(time, initTime[i]) == 1) {
time -= initTime[i]; ++cnt;
cnt += (long long)floor(time / crossTime[i]);
}
return cnt;
};
while (R - L > eps) {
mid = 0.5 * (L + R);
long long num = 0;
for (int i = 0; i < 3; ++i) num += cal(i, mid);
if (num >= k) R = mid;
else L = mid;
}
cout << fixed << setprecision(10) << mid / sqrt(vx * vx + vy * vy) << '\n';
}
return 0;
}
1009 Parentheses Matching
首先将从右到左遍历,将'('和最近的')'进行匹配消除,将无法消除的括号分别加入栈和队列中。
此时剩余的'('都在')'右侧,那么剩下的只要考虑'*'和括号的匹配即可。
#include
using namespace std;
const int maxn = 1e5 + 5;
char s[maxn];
int main() {
int t;
scanf("%d", &t);
while (t--) {
scanf("%s", s + 1);
int n = strlen(s + 1);
stacks1;
queues2;
for (int i = n; i > 0; i--) {
if (s[i] == ')') s1.push(i);
else if (s[i] == '(') {
if (!s1.empty()) s1.pop();
else s2.push(i);
}
}
for (int i = 1; i <= n; i++) {
if (s1.empty()) break;
if (s[i] == '*') {
int x = s1.top();
if (i < x) {
s[i] = '(';
s1.pop();
}
}
}
for (int i = n; i >= 1; i--) {
if (s2.empty()) break;
if (s[i] == '*') {
int x = s2.front();
if (i > x) {
s[i] = ')';
s2.pop();
}
}
}
if ((!s1.empty()) || (!s2.empty())) {
printf("No solution!\n");
}
else {
for (int i = 1; i <= n; i++) {
if (s[i] != '*') printf("%c", s[i]);
}
printf("\n");
}
}
return 0;
}