看了就明白，KMP算法乱弹～～

http://www.inf.fh-flensburg.de/lang/algorithmen/pattern/kmpen.htm

http://www.ics.uci.edu/~eppstein/161/960227.html

T为主串ababaaababaaababaa，大小为18；p为模式串ababaa，大小为6；

不免俗的我们先看下，普通的字符串匹配算法核心代码：

    for (i=0; T[i] != '\0'; i++)
    {
         for (j=0; T[i+j] != '\0' && P[j] != '\0' && T[i+j]==P[j]; j++)
                ; //这有个分号哟。
             if (P[j] == '\0')
               {
                     report(i);//找到了一个匹配的
               }
    }

外循环主串索引i每次++，共18次，一路加到底。每次内循环模式串的索引j 变化范围不定。最坏为6次++运算。 算法的最坏情况18*6

KMP算法：

先看几个概念：

前缀串：

A prefix of x is a substring u with  u  =  x₀ ... x_b-1   where  b  {0, ..., k} i.e. x starts with u.

后缀串：

A suffix of x is a substring u with u  =  x_k-b ... x_k-1   where  b  {0, ..., k} i.e. x ends with u.

真前缀串和真后缀串：

A prefix u of x or a suffix u of x is called a proper prefix or suffix, respectively, if ux, i.e. if its length b is less than k.

边界串：

A border of x is a substring r with  r  =  x₀ ... x_b-1  and  r  =  x_k-b ... x_k-1   where  b  {0, ..., k-1} 

注意，边界串的定义是必须同时满足  真前缀串和真后缀串 的字符串才能被称作 边界串！！通俗点，边界串就是两头相等的前后缀串的合体。

r 和 s 都是边界串！

边界串扩展：

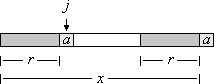
Let x be a string and a  A a symbol. A border r of x can be extended by a, if ra is a border of xa.

下图中r边界串被扩展成ra边界串了。

下面的代码中：

数组b[]就是我们求出的模式串中每个元素的border值——就是边界串的长度。

好吧，让我们从头说起，话说不知那一天高德纳老爷爷，抱怨 普通字符串匹配算法效率太差了，就想改进他，怎么改进他呢?

本质上就是减少普通字符串匹配算法中内外曾循环的次数，这就用到了边界串了！

在下面的代码中，我们看到外层循环索引还是++ 了18次。

改变的是内层的循环次数，至于怎么减少的自己理解去吧！还用说就是用着个border值呗！border值就是网上的next值是也！

那，这个border值怎么求的？请跳到下一段。

void kmpSearch()
{
    int i=0, j=0;//i为主串索引，j为模式串索引
    for ( ;i < 18; )//你瞧，和普通的字符串匹配算法多像呀:-)
    {
        for ( ; j>=0 && T[i]!=p[j]; ) 
          j=b[j];  //就是这里了提高了效率
          i++; j++;
        if (j==m)
        {
            report(i-j);// 找到了，i-j 为模式串在主串最初出现的位置。
            j=b[j];
        }
    }
}

KMP算的核心组件：预处理 算法

把下面这句看懂了，border 你就懂了。

The preprocessing algorithm comprises a loop with a variable j assuming these values. A border of width j can be extended by p_i, ifp_j = p_i. If not, the next-widest border is examined by setting j = b[j]. The loop terminates at the latest if no border can be extended (j = -1).

void kmpPreprocess() //求模式串中每个元素的border值。
{
    int i=0, j=-1;//i为模式串的索引，j为当前处理到第i个模式串中的元素的border值。
    b[i]=j; //b[] 是全局数组
    while (i=0 && p[i]!=p[j]) j=b[j]; //这句是核心请举例画图，就可以明白配合上面的英文解释。
        i++; j++;
        b[i]=j;
    }
}