前言
欧拉序其实是一个很好用的东西,可以方便地求一些树上位置关系。
但是为什么没人用呢?
一、什么是欧拉序
欧拉序是在将一棵树转为一个序列,这个序列就叫欧拉序。
从根结点开始进行深度优先搜索,对于每个结点,入栈时和出栈时都记录一次。
例如下面这棵以1为根的树:
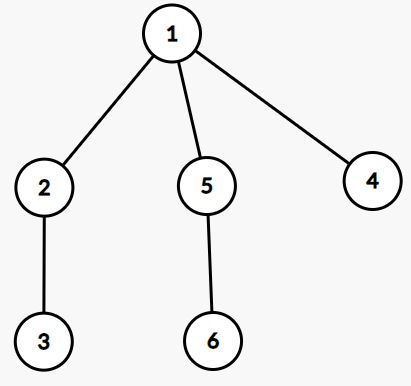
它的欧拉序为:123325665441,长度为2n
二、欧拉序判定树上位置关系
下面,我们以模板题祖孙询问来说明欧拉序如何判断位置关系。
对于每个点,我们开两个数组ein与eout来记录每个点的入栈和出栈时在欧拉序中是第几个。
还是以上图为例,那么
ein:1 2 3 10 6 7
eout:12 5 4 11 9 8
不难发现,一个点x是y的祖先,当且仅当x比y早入栈且x比y晚出栈。
即ein[x]<=ein[y] and eout[x]>=eout[y]
这里用了等于是如果x=y了,那么也算是祖先,避免了这种情况。
于是程序就很容易写出来了:
#include
#include
using namespace std;
const int N=1e5+5;
int n,m;
int head[N],to[N],nxt[N],cnt;
int ein[N],eout[N],tot,root;
void add(int x,int y) { //链式前向星
to[++cnt]=y;
nxt[cnt]=head[x];
head[x]=cnt;
}
void dfs(int x) {
ein[x]=++tot; //tot用了计数,这里记录下x的入栈时间
for(int i=head[x];i;i=nxt[i]) {
int y=to[i];
if(!ein[y]) //如果y没访问过,就dfs(y)
dfs(y);
}
eout[x]=++tot; //记录x的出栈时间
}
bool up(int x,int y) { //即上面的那串代码
return (ein[x]<=ein[y] and eout[x]>=eout[y]);
}
int main() {
cin>>n;
for(int i=1;i<=n;i++) {
int x,y;
cin>>x>>y;
if(y!=-1) { //判断根结点
add(x,y);
add(y,x);
}
else root=x;
}
dfs(root); //生成欧拉序
cin>>m;
while(m--) {
int x,y;
cin>>x>>y;
if(up(x,y)) //x是y的祖先
cout<<1< 并且,这个程序的时间复杂度是\(O(n+m)\)比求LCA判定祖孙关系的时间复杂度\(O(mlogn)\)要好很多(如果你用tarjan求LCA当我没说,但个人觉得tarjan常数比欧拉序要大)。
三、LCA的写法
1、欧拉序+ST表
众所周知LCA是倍增来写的,其实还可以用欧拉序+ST表来实现,单次询问时间复杂度是\(O(1)\)的,比对数要快。
但因为写起来有点麻烦,就不写了。
2、倍增+祖孙判定
当然欧拉序可能更加帮你容易懂倍增LCA,它是这样子来写的。
我们先看预处理的部分
void dfs(int x,int fa) { //x的父亲是fa结点
f[x][0]=fa;
for(int i=1;i<=h;i++) //预处理倍增数组,这个少不了
f[x][i]=f[f[x][i-1]][i-1];
d[x]=d[fa]+1;
//求欧拉序每个点的进出时间
ein[x]=++tot;
for(int i=head[x];i;i=nxt[i]) {
int y=to[i];
if(y!=fa)
dfs(y,x);
}
eout[x]=++tot;
}
然后就是LCA了
int lca(int x,int y) {
//两种特殊情况
if(up(x,y))
return x;
if(up(y,x))
return y;
for(int i=h;i>=0;i--)
if(!up(f[x][i],y) and f[x][i]!=0) //如果不是祖先,又不是0号结点
x=f[x][i]; //往上跳
return f[x][0]; //最后x的父亲必定是x与y的LCA
}
用祖孙判定+倍增来写是何等的简洁!比一起跳的那种倍增LCA要易懂得多(个人这么认为)。
点的距离AC代码
#include
#include
using namespace std;
const int N=2e5+5;
int n,m,h;
int head[N],to[N],nxt[N],cnt;
int ein[N],eout[N],tot;
int d[N],f[N][21];
void add(int x,int y) {
to[++cnt]=y;
nxt[cnt]=head[x];
head[x]=cnt;
}
void dfs(int x,int fa) {
f[x][0]=fa;
for(int i=1;i<=h;i++)
f[x][i]=f[f[x][i-1]][i-1];
d[x]=d[fa]+1; //树上前缀和
ein[x]=++tot;
for(int i=head[x];i;i=nxt[i]) {
int y=to[i];
if(y!=fa)
dfs(y,x);
}
eout[x]=++tot;
}
bool up(int x,int y) {
return (ein[x]<=ein[y] and eout[x]>=eout[y]);
}
int lca(int x,int y) {
if(up(x,y))
return x;
if(up(y,x))
return y;
for(int i=h;i>=0;i--)
if(!up(f[x][i],y) and f[x][i]!=0)
x=f[x][i];
return f[x][0];
}
int main() {
cin>>n;
h=log(n)/log(2)+1; //深度
for(int i=1;i>x>>y;
add(x,y);
add(y,x);
}
dfs(1,0); //处理欧拉序
cin>>m;
while(m--) {
int x,y;
cin>>x>>y;
cout< 四、换根
这种欧拉序就比较神奇了,它是每经过一个点就记录一次,所以说可能一个点的次数不止两次。

还是以刚才那张图为例,这样子以1为根的欧拉序为:12321565141
这种欧拉序有着“循环”的功能,我们不妨将这串欧拉序延长一倍:123215651412321565141
那么换做是以5为根呢?欧拉序为刚才那个两倍串中标粗的一段:123215651412321565141
不管你换成以哪个点为根,都是一样的。所以就可以很方便地求解一些换根的操作啦。
但是程序实现较困难,所以就不写了qwq。