顺序表示的队列——顺序队列1——基本内容

队列

队列是一种受限的线性表。它只允许在表的一端进行插入，另一端进行删除。队列具有“先入先出”的特性，它的应用非常广泛，它主要应用在树的层次遍历、图的广度优先遍历、键盘的输入缓冲区、操作系统和事务管理等方面。

【定义】

队列（queue）是一种先进先出（First In First Out , FIFO）的线性表，它只允许在表的一端插入元素，另一端删除元素。其中，允许插入的一端称为队尾（rear），允许删除的一端称为对头（front）。

一个队列为q=(a1,a2,...,an), 如图

 那么a1为对头元素，an为队尾元素。最早进入队列的元素也会最早出来，只有当最先进入队列的元素都出来以后，后进入的元素才能退出。

在日常生活中，人们去银行办理业务需要排队，这就类似我们提到的队列。每一个新来办理业务的需要按照机器自动生成的编号等待办理，只有前面的人办理完毕，才能轮到排在后面的人办理业务。新来的人进入排队状态就相当于入队，前面办理完业务离开的就相当于出队。
队列有两种存储表示：顺序存储和链式存储。采用顺序存储结构的队列被称为顺序队列，采用链式存储结构的队列称为链式队列。

【顺序队列】

顺序队列通常采用一维数组存储队列中的元素，另外增加两个指针分别指示数组中存放的队首元素和队尾元素。其中指向队首元素的指针称为队头指针front，指向队尾元素的指针称为队尾指针rear。
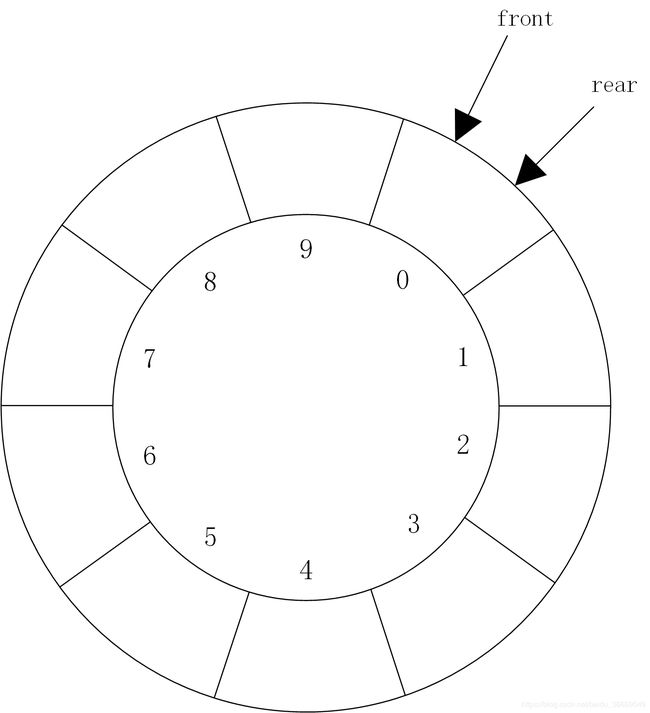
队列为空时，队头指针front和队尾指针rear都指向下标为0的存储单元，当元素a,b,c,d,e,f,g依次进入队列后，元素a~g分别存放在数组下标为0~6的存储单元中，队头指针front指向元素a，队尾指针指rear向元素g的下一位置。如图所示。
 

【假溢出】

但是按照前面介绍的顺序存储方式，容易出现“假溢出”。所谓“假溢出”，就是经过多次插入和删除操作后，实际队列还有存储空间，但是又无法向队列中插入元素。
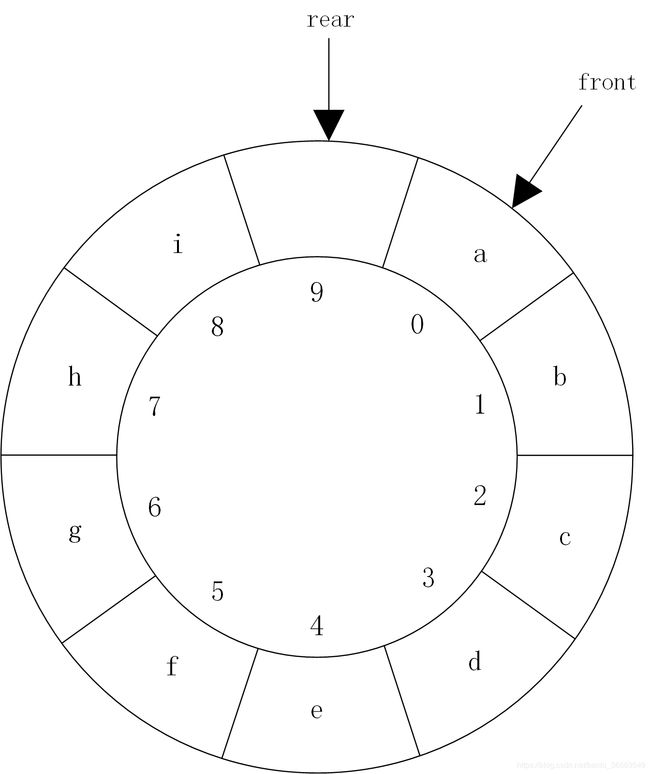
例如在图中队列删除a和b，然后依次插入h、i和j，当插入j后，就会出现队尾指针rear越出数组的下界造成“假溢出”，如图

 

 

【顺序循环队列】

当队尾指针rear或队头指针front到达存储空间的最大值时（假定队列的存储空间为QueueSize），让队尾指针或者队头指针转化为0，这样就可以将元素插入到队列的空闲存储单元中，有效的利用存储空间，消除“假溢出”。
例如在上面的例子中，插入元素j后，rear将变为0，这样就将j插入下标为0的存储单元中。这样顺序队列的存储空间就构成了一个逻辑上收尾相连的循环队列。
要把用数组表示的顺序队列构成循环队列，只需要一个简单的取余操作即可实现。例如当队尾指针rear=9（假设QueueSize=10）时，如果要将新元素入队，则先令rear=（rear+1）%10,这样rear就等于0，这样利用取余操作就实现了队列逻辑上的首尾相连，然后将元素存入队列的第0号单元。

【队空和队满】

在循环队列中，队空和队满时队头front和队尾指针rear同时都会指向同一存储单元，即front==rear，如图所示。

队空 

队满 

如何区分队空和队满呢？有以下两种方法：

（1）增加一个标志位。设标志位为tag,初始时，tag=0;当入队成功，则tag=1；出队成功，tag=0。则判断队空的条件为：front==rear&&tag==0;队满的条件为：front==rear&&tag==1;
（2）少用一个存储单元。队空的判断条件为front==rear；队满的判断条件为front==(rear+1）%QueueSize。
队满的状态如图。
 

【存储结构】

typedef struct Squeue
{
	DataType queue[QueueSize];
	int front, rear;
}SeqQueue;

【基本运算】

（1）初始化队列

void InitQueue(SeqQueue *SCQ)
{
	SCQ->front = SCQ->rear = 0;
}

（2）判断队列是否为空

int QueueEmpty(SeqQueue SCQ)
{
	if (SCQ.front==SCQ.rear)
	{
		return 1;

	}
	else
	{
		return 0;
	}
}

（3）将元素e入队

int EnQueue(SeqQueue *SCQ, DataType e)
{
	if (SCQ->front==(SCQ->rear+1)%QueueSize)
	{
		return 0;
	}
	SCQ->queue[SCQ->rear] = e;
	SCQ->rear = (SCQ->rear + 1) % QueueSize;
	return 1;
}

（4）队头元素出队

int DeQueue(SeqQueue *SCQ, DataType *e)
{
	if (SCQ->front==SCQ->rear)
	{
		return 0;
	}
	else
	{
		*e = SCQ->queue[SCQ->front];
		SCQ->front = (SCQ->front + 1) % QueueSize;
		return 1;
	}
}

（5）取队头元素

int GetHead(SeqQueue SCQ, DataType *e)
{
	if (SCQ.front==SCQ.rear)
	{
		return 0;
	}
	else
	{
		*e = SCQ.queue[SCQ.front];
		return 1;
	}
}

（6）清空队列

void ClearQueue(SeqQueue *SCQ)
{
	SCQ->front = SCQ->rear = 0;

}