【转】PCL学习-点云分割-基于DoN的点云分割
类 pcl::DifferenceOfNormalsEstimation提供了一种根据不同尺度下法向量特征的差异性的点云分割方法,即DoN(Difference of Normals)算法。
DoN算法:
DoN特征源于观察到基于所给半径估计的表面法向量可以反映曲面的内在几何特征,因此这种分割算法是基于法线估计的,需要计算点云中某一点的法线估计。而通常在计算法线估计的时候都会用到邻域信息,很明显邻域大小的选取会影响法线估计的结果。而在DoN算法中,邻域选择的大小就被称为support radius(支持半径)。对点云中某一点选取不同的支持半径,即可以得到不同的法线估计,而法线之间的差异,就是是所说的法线差异(Difference of Normals)。
图1 支撑半径对输入点云估计的表面法线的影响
对于点云中的每个点,估计两个单位点法线具有不同的半径,. 这些点法线的归一化(向量)差异定义了算子。
DoN特征算子定义如下:
其中,和是给定支撑半径的点的表面法线估计。请注意,算子的响应是一个归一化的矢量场,因此是可定向的(结果方向是一个关键特征),然而,该算子的范数提供了一个更易操作的量化方式,并且始终在该范围内。
备注:
- 法线估计:用利用固定支持半径的方法来估计,而不能使用那种利用固定邻域点数目的方法。
- 法线方向歧义消除:对于DoN操作的特定应用,只要以相同的方式消除两个支持半径的歧义,就不会出现问题了。具体做法就是:如果两条法线之间的夹角大于90°,则假定真实的法线彼此之间的夹角小于90°。
分割步骤:
(1)对于输入点云数据中的每一点,利用较大的支撑半径rl计算法向量;
(2)对于输入点云数据中的每一点,利用较大的支撑半径rs计算法向量;
(3)对于输入点云数据中的每一点,单位化每一点的法向量差异,计算公式如下:
(4)过滤所得的向量域(DoN特征向量),分割出目标尺寸对应的点云; 为了分割点云,必须利用DoN特征向量的计算结果区分点云,常用的一些量化标准如下表:
| 量化标准 | 点的法向量域 | 描述 | 使用场景 |
|---|---|---|---|
| float normal[3] | DoN vector | 通过DoN相对角度分类; | |
| float curvature | DoN norm | 通过尺度效应进行滤波,较大的模对输入尺度参数有较大效应; | |
| , | float normal[0] | DoN vector x component | 利用方向尺度(orientable scale)进行滤波, 比如建筑物外墙有较大的 或者 和较小的 |
| , | float normal[1] | DoN vector y component | |
| , | float normal[2] | DoN vector z component |
测试示例:
流程说明:
1. 计算大小支撑半径;
2. 最对大小支撑半径进行点云法线估计;
3. 计算DoN特征向量;
4. 对曲率特征,进行条件滤波;
5. 基于欧式距离进行分割;
/**
* @file don_segmentation.cpp
* Difference of Normals Example for PCL Segmentation Tutorials.
*
* @author Yani Ioannou
* @date 2012-09-24
* @修改 2015-6-16
*/
#include ne;
pcl::NormalEstimation<PointXYZRGB, PointNormal> ne;
ne.setInputCloud(cloud);
ne.setSearchMethod(tree);
/**
* NOTE: setting viewpoint is very important, so that we can ensure
* normals are all pointed in the same direction!
*/
ne.setViewPoint(std::numeric_limits<float>::max(), std::numeric_limits<float>::max(), std::numeric_limits<float>::max());
// calculate normals with the small scale
cout << "Calculating normals for scale..." << scale1 << endl;
pcl::PointCloud<PointNormal>::Ptr normals_small_scale(new pcl::PointCloud<PointNormal>);
ne.setRadiusSearch(scale1);
ne.compute(*normals_small_scale);
// calculate normals with the large scale
cout << "Calculating normals for scale..." << scale2 << endl;
pcl::PointCloud<PointNormal>::Ptr normals_large_scale(new pcl::PointCloud<PointNormal>);
ne.setRadiusSearch(scale2);
ne.compute(*normals_large_scale);
//visualize the normals
if (VISUAL = 1)
{
cout << "click q key to quit the visualizer and continue!!" << endl;
boost::shared_ptr<pcl::visualization::PCLVisualizer> MView(new pcl::visualization::PCLVisualizer("Showing normals with different scale"));
pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZRGB> green(cloud, 0, 255, 0);
int v1(0), v2(0);
MView->createViewPort(0.0, 0.0, 0.5, 1.0, v1);
MView->createViewPort(0.5, 0.0, 1.0, 1.0, v2);
MView->setBackgroundColor(1, 1, 1);
MView->addPointCloud(cloud, green, "small_scale", v1);
MView->addPointCloud(cloud, green, "large_scale", v2);
MView->addPointCloudNormals<pcl::PointXYZRGB, pcl::PointNormal>(cloud, normals_small_scale, 100, mean_radius * 10, "small_scale_normal");
MView->addPointCloudNormals<pcl::PointXYZRGB, pcl::PointNormal>(cloud, normals_large_scale, 100, mean_radius * 10, "large_scale_normal");
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 3, "small_scale", v1);
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_OPACITY, 0.5, "small_scale", v1);
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 3, "large_scale", v1);
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_OPACITY, 0.5, "large_scale", v1);
MView->spin();
}
// Create output cloud for DoN results
PointCloud<PointNormal>::Ptr doncloud(new pcl::PointCloud<PointNormal>);
copyPointCloud<PointXYZRGB, PointNormal>(*cloud, *doncloud);
cout << "Calculating DoN... " << endl;
// Create DoN operator
pcl::DifferenceOfNormalsEstimation<PointXYZRGB, PointNormal, PointNormal> don;
don.setInputCloud(cloud);
don.setNormalScaleLarge(normals_large_scale);
don.setNormalScaleSmall(normals_small_scale);
if (!don.initCompute())
{
std::cerr << "Error: Could not intialize DoN feature operator" << std::endl;
exit(EXIT_FAILURE);
}
// Compute DoN
don.computeFeature(*doncloud);
//print some differencense of curvature
{
cout << "You may have some sense about the input threshold(curvature) next time for your data" << endl;
int size_cloud = doncloud->size();
int step = size_cloud / 10;
for (int i = 0; i < size_cloud; i += step)cout << " " << doncloud->points[i].curvature << " " << endl;
}
//show the differences of curvature with both large and small scale
if (VISUAL = 1)
{
cout << "click q key to quit the visualizer and continue!!" << endl;
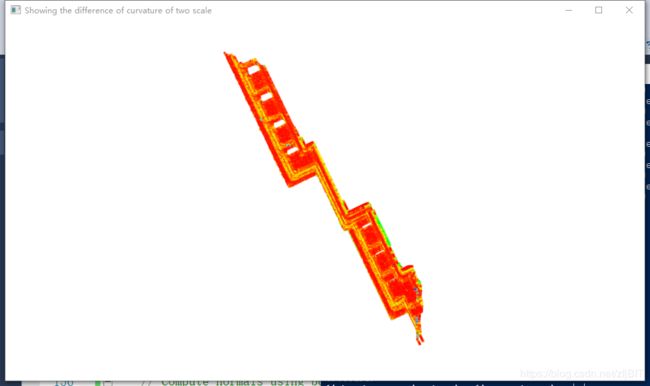
boost::shared_ptr<pcl::visualization::PCLVisualizer> MView(new pcl::visualization::PCLVisualizer("Showing the difference of curvature of two scale"));
pcl::visualization::PointCloudColorHandlerGenericField<pcl::PointNormal> handler_k(doncloud, "curvature");
MView->setBackgroundColor(1, 1, 1);
MView->addPointCloud(doncloud, handler_k);
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 3);
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_OPACITY, 0.5);
MView->spin();
}
// Save DoN features
pcl::PCDWriter writer;
if (SAVE == 1) writer.write<pcl::PointNormal>("don.pcd", *doncloud, false);
// Filter by magnitude
cout << "Filtering out DoN mag <= " << threshold << "..." << endl;
//创建条件滤波函数
pcl::ConditionOr<PointNormal>::Ptr range_cond(
new pcl::ConditionOr<PointNormal>()
);//确定点是否属于满足设定的条件
range_cond->addComparison(pcl::FieldComparison<PointNormal>::ConstPtr(
new pcl::FieldComparison<PointNormal>("curvature", pcl::ComparisonOps::GT, threshold))
);//添加比较条件
pcl::ConditionalRemoval<PointNormal> condrem(range_cond);//建立条件滤波器
condrem.setInputCloud(doncloud);//设置输入点云
pcl::PointCloud<PointNormal>::Ptr doncloud_filtered(new pcl::PointCloud<PointNormal>);
// Apply filter
condrem.filter(*doncloud_filtered);
doncloud = doncloud_filtered;
// Save filtered output
std::cout << "Filtered Pointcloud: " << doncloud->points.size() << " data points." << std::endl;
if (SAVE == 1)writer.write<pcl::PointNormal>("don_filtered.pcd", *doncloud, false);
//show the results of keeping relative small curvature points
if (VISUAL == 1)
{
cout << "click q key to quit the visualizer and continue!!" << endl;
boost::shared_ptr<pcl::visualization::PCLVisualizer> MView(new pcl::visualization::PCLVisualizer("Showing the results of keeping relative small curvature points"));
pcl::visualization::PointCloudColorHandlerGenericField<pcl::PointNormal> handler_k(doncloud, "curvature");
MView->setBackgroundColor(1, 1, 1);
MView->addPointCloud(doncloud, handler_k);
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 3);
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_OPACITY, 0.5);
MView->spin();
}
// Filter by magnitude
cout << "Clustering using EuclideanClusterExtraction with tolerance <= " << segradius << "..." << endl;
pcl::search::KdTree<PointNormal>::Ptr segtree(new pcl::search::KdTree<PointNormal>);
segtree->setInputCloud(doncloud);
std::vector<pcl::PointIndices> cluster_indices;
pcl::EuclideanClusterExtraction<PointNormal> ec;
ec.setClusterTolerance(segradius);
ec.setMinClusterSize(50);
ec.setMaxClusterSize(100000);
ec.setSearchMethod(segtree);
ec.setInputCloud(doncloud);
ec.extract(cluster_indices);
if (VISUAL == 1)
{//visualize the clustering results
pcl::PointCloud <pcl::PointXYZ>::Ptr tmp_xyz(new pcl::PointCloud<pcl::PointXYZ>);
copyPointCloud<pcl::PointNormal, pcl::PointXYZ>(*doncloud, *tmp_xyz);
pcl::PointCloud <pcl::PointXYZRGB>::Ptr colored_cloud = getColoredCloud(tmp_xyz, cluster_indices, 0, 255, 0);
cout << "click q key to quit the visualizer and continue!!" << endl;
boost::shared_ptr<pcl::visualization::PCLVisualizer> MView(new pcl::visualization::PCLVisualizer("visualize the clustering results"));
pcl::visualization::PointCloudColorHandlerRGBField<pcl::PointXYZRGB> rgbps(colored_cloud);
MView->setBackgroundColor(1, 1, 1);
MView->addPointCloud(colored_cloud, rgbps);
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 3);
MView->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_OPACITY, 0.5);
MView->spin();
}
if (SAVE == 1)
{
int j = 0;
for (std::vector<pcl::PointIndices>::const_iterator it = cluster_indices.begin(); it != cluster_indices.end(); ++it, j++)
{
pcl::PointCloud<PointNormal>::Ptr cloud_cluster_don(new pcl::PointCloud<PointNormal>);
for (std::vector<int>::const_iterator pit = it->indices.begin(); pit != it->indices.end(); ++pit)
{
cloud_cluster_don->points.push_back(doncloud->points[*pit]);
}
cloud_cluster_don->width = int(cloud_cluster_don->points.size());
cloud_cluster_don->height = 1;
cloud_cluster_don->is_dense = true;
//Save cluster
cout << "PointCloud representing the Cluster: " << cloud_cluster_don->points.size() << " data points." << std::endl;
stringstream ss;
ss << "don_cluster_" << j << ".pcd";
writer.write<pcl::PointNormal>(ss.str(), *cloud_cluster_don, false);
}
}
}
> .\don_segmentation.exe ..\..\source\region_growing_tutorial.pcd 5 10 0.3 10 1 0
mean radius of cloud is: 7.1868
Calculating normals for scale...35.934
Calculating normals for scale...71.868
click q key to quit the visualizer and continue!!
Calculating DoN...
You may have some sense about the input threshold(curvature) next time for your data
0.134399
0.237334
0.00346533
0.0607801
0.191838
0.0546108
0.092865
0.0907592
0.0801567
0.0337127
0.0664349
click q key to quit the visualizer and continue!!
Filtering out DoN mag <= 0.3...
Filtered Pointcloud: 3034 data points.
click q key to quit the visualizer and continue!!
Clustering using EuclideanClusterExtraction with tolerance <= 71.868...
click q key to quit the visualizer and continue!!
可视化结果:
(a)曲率信息可视化 (b) 利用曲率分类可视化 (c)欧式聚类分割结果