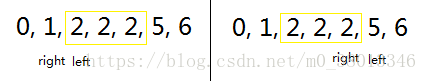二分查找算法分析-我真的不会写二分啊
1 二分查找
二分查找是一个基础的算法,也是面试中常考的一个知识点。二分查找就是将查找的键和子数组的中间键作比较,如果被查找的键小于中间键,就在左子数组继续查找;如果大于中间键,就在右子数组中查找,否则中间键就是要找的元素。
///二分查找
int binarysearch(int arr[],int len,int key)
{
int left = 0,right = len-1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key < arr[mid]) right = mid - 1;
else if(key > arr[mid]) left = mid + 1;
else return mid;
}
return -1;
}注意到我们这样写的原因对于left和right,在判断完当前的mid时都要进行加1或者减1的操作,防止出现死循环,
注意:代码中的判断条件必须是while (left <= right),否则的话判断条件不完整,比如:array[3] = {1, 3, 5};待查找的键为5,此时在(low < high)条件下就会找不到,因为low和high相等时,指向元素5,但是此时条件不成立,没有进入while()中。
2 二分查找的变种
对于二分查找的题中,并不是数组的元素是唯一的,元素可能出现重复.于是就产生了以下几种变形
主要是这两种 - 以下默认序列是非递减序列
- 寻找最小解,最小最优
- 寻找最大解,最大最优
对于寻找最小解的:当key = arr[mid]时,应该向左边的搜索,因为左边可能还存在更优的解.
对应的上图左图,最后的left和right应该呈上图标记,(因为循环中是left <= right) 则终止条件为left > right ,而由于只加1减1所以
left只会比right大1.
而对于最后可行解mid来说,right = mid - 1,最终right一定不是可行解,但mid一定是最小可行解,而left = right + 1 = mid
于是我们可以得到:
right : 最后一个小于key的元素,(下界最后一个不满足解的元素)
left : 第一个大于等于key的元素,(当存在解时,left就是最小解) < = > 对应与lower_bound函数
对应的代码
///查找最后一个小于key的元素
int findLastLess(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key <= arr[mid]) right = mid - 1;
else left = mid + 1;
}
return right;
}
///查找第一个大于等于key的元素
int findFirstGreaterEqual(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key <= arr[mid]) right = mid - 1;
else left = mid + 1;
}
return left;
}对于寻找最大解的:当key = arr[mid]时,应该向右边的搜索,因为左边可能还存在更优的解.
对应与上图右.
同理可以得到
right : 最后一个小于等于key的元素,(当存在解时,right就是最大解)
left : 第一个大于key的元素,(上界第一个不满足解的元素) < = > 对应与upper_bound函数
对应代码为
///查找最后一个小于等于key的元素
int findLastLessEqual(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key < arr[mid]) right = mid - 1;
else left = mid + 1;
}
return right;
}
///查找第一个大于key的元素
int findFirstGreater(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key < arr[mid]) right = mid - 1;
else left = mid + 1;
}
return left;
}其实也很好记:只要想到最终跳出时left要比right大1,
在寻找最小解时,right为最小解,而left比right小,则left是下界最后一个非解
在寻找最大解时,left为最大解,而right比left大,则right是上界的第一个非解.
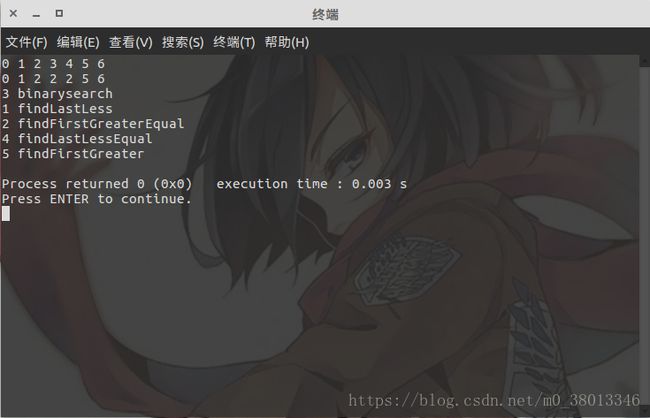
最后给出测试代码
#include
using namespace std;
///二分查找
int binarysearch(int arr[],int len,int key)
{
int left = 0,right = len-1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key < arr[mid]) right = mid - 1;
else if(key > arr[mid]) left = mid + 1;
else return mid;
}
return -1;
}
///查找最后一个小于key的元素
int findLastLess(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key <= arr[mid]) right = mid - 1;
else left = mid + 1;
}
return right;
}
///查找第一个大于等于key的元素
int findFirstGreaterEqual(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key <= arr[mid]) right = mid - 1;
else left = mid + 1;
}
return left;
}
///查找最后一个小于等于key的元素
int findLastLessEqual(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key < arr[mid]) right = mid - 1;
else left = mid + 1;
}
return right;
}
///查找第一个大于key的元素
int findFirstGreater(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key < arr[mid]) right = mid - 1;
else left = mid + 1;
}
return left;
}
///查找第一个等于key的元素,如果没有返回-1
int findFirstEqual(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key <= arr[mid]) right = mid - 1;
else right = mid + 1;
}
///left = findFirstGreaterEqual(arr,len,key);
///注意:此时right是最后一个小于key的元素,left是第一个大于等于key的值
///于是只需要判断left元素是不是等于key就好
if(left < len && arr[left] == key) return left;
return -1;
}
///查找最后一个等于key的元素,如果没有返回-1
int findLastEqual(int arr[],int len,int key)
{
int left = 0,right = len - 1,mid;
while(left <= right) {
mid = (left + right) >> 1;
if(key < arr[mid]) right = mid - 1;
else left = mid + 1;
}
///right = findLastLessEqual(arr,len,key);
///注意:此时right是最后一个小于等于key的元素,left是第一个大于key的值
///于是只需要判断right元素是不是等于key就好
if(right >= 0 && arr[right] == key) return right;
return -1;
}
void test()
{
int arr[] = {0,1,2,2,2,5,6};
int len = 7,key = 2,index,i ;
for(int i=0;i