C#-数据结构-图的应用 普里姆算法和克鲁斯卡尔算法

6.4.1 最小生成树 

1、小生成树的基本概念

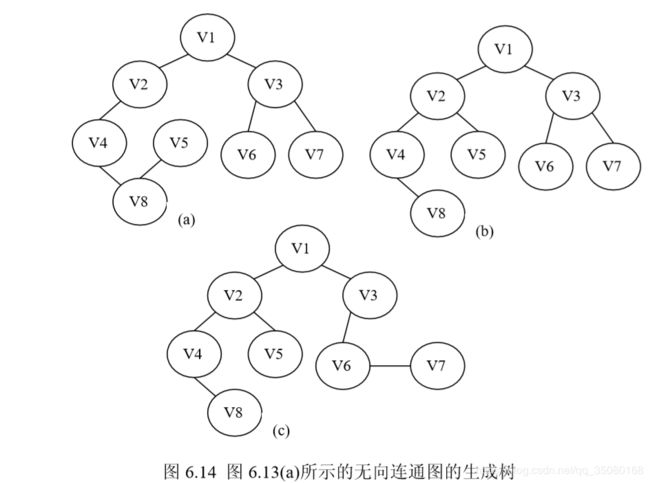
 由生成树的定义可知，无向连通图的生成树不是唯一的，对连通图的不同遍 历就得到不同的生成树。图 6.14 所示是图 6.13(a)所示的无向连通图的部分生成 树。 
数

 

 

 

如果是一个无向连通网，那么它的所有生成树中必有一棵边的权值总和小 的生成树，我们称这棵生成树为小代价生成树(Minimum Cost Spanning Tree)， 简称小生成树。 

许多应用问题都是一个求无向连通网的小生成树问题。例如，要在 n 个城 市之间铺设光缆，铺设光缆的费用很高，并且各个城市之间铺设光缆的费用不同。 一个目标是要使这 n 个城市的任意两个之间都可以直接或间接通信，另一个目标 是要使铺设光缆的总费用低。如果把 n 个城市看作是图的 n 个顶点，两个城市 之间铺设的光缆看作是两个顶点之间的边，这实际上就是求一个无向连通网的 小生成树问题。

由小生成树的定义可知，构造有 n 个顶点的无向连通网的小生成树必须 满足以下三个条件： 

（1）构造的小生成树必须包括 n 个顶点；

（2）构造的小生成树有且仅有 n-1 条边；

（3）构造的小生成树中不存在回路。 

构造小生成树的方法有许多种，典型的方法有两种，一种是普里姆(Prim) 算法，一种是克鲁斯卡尔(Kruskal)算法。 

2、普里姆(Prim)算法 

假设 G=（V，E）为一无向连通网，其中，V 为网中顶点的集合，E 为网中 边的集合。设置两个新的集合 U 和 T，其中，U 为 G 的小生成树的顶点的集 合，T 为 G 的小生成树的边的集合。普里姆算法的思想是：令集合 U 的初值 为 U={u1}（假设构造小生成树时从顶点 u1 开始），集合 T 的初值为 T={}。从 所有的顶点 u∈U 和顶点 v∈V-U 的带权边中选出具有小权值的边（u,v），将顶 点 v 加入集合 U 中，将边（u,v）加入集合 T 中。如此不断地重复直到 U=V 时， 小生成树构造完毕。此时，集合 U 中存放着小生成树的所有顶点，集合 T中存放着小生成树的所有边。 

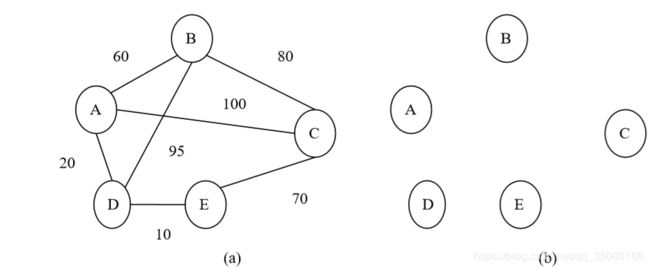
【例 6-3】以图 6.2(a)为例，说明用普里姆算法构造图的无向连通网的小 生成树的过程。 

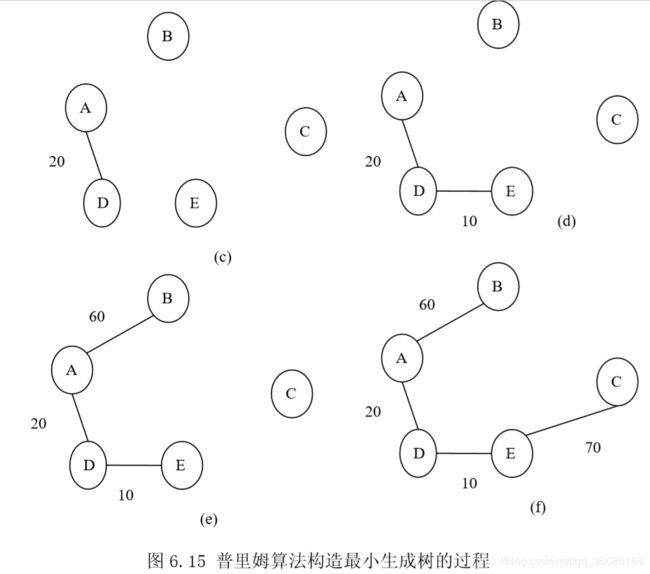
为了分析问题的方便，把图 6.2(a)中所示的无向连通网重新画在图 6.15 中， 如图 6.15(a)所示。初始时，算法的集合 U={A}，集合 V-U={B,C,D,E}，集合 T={}， 如图 6.15(b)所示。在所有 u 为集合 U 中顶点、v 为集合 V-U 中顶点的边(u,v)中 寻找具有小权值的边，寻找到的边是(A,D)，权值为 20，把顶点 B 加入到集合 U 中，把边(A,D)加入到集合 T 中，如图 6.15(c)所示。在所有 u 为集合 U 中顶点、 v 为集合 V-U 中顶点的边(u,v)中寻找具有小权值的边，寻找到的边是(D,E)，权 值为 10，把顶点 E 加入到集合 U 中，把边(D,E)加入到集合 T 中，如图 6.15(d) 所示。随后依次从集合 V-U 中加入到集合 U 中的顶点为 B、C，依次加入到集合 T 中的边为(A,B)（权值为 60）、(E,C) （权值为 70），分别如图 6.15(e)、(f)所示。 后得到的图 6.15(f)所示就是原无向连通网的小生成树。 

 

 

本书以无向网的邻接矩阵类 NetAdjMatrix来实现普里姆算法。 NetAdjMatrix类的成员字段与无向图邻接矩阵类 GraphAdjMatrix的成员 字段一样，不同的是，当两个顶点间有边相连接时，matirx 数组中相应元素的值 是边的权值，而不是 1。 

无向网邻接矩阵类 NetAdjMatrix的实现如下所示。 

public class NetAdjMatrix : IGraphs
{
    private Node[] nodes;      //顶点数组 
    private int numEdges;         //边的数目
    private int[,] matrix;       //邻接矩阵数组 

    //构造器 
    public NetAdjMatrix(int n)
    {
        nodes = new Node[n];
        matrix = new int[n, n];
        numEdges = 0;
    }

    //获取索引为index的顶点的信息 
    public Node GetNode(int index)
    {
        return nodes[index];
    }

    //设置索引为index的顶点的信息 
    public void SetNode(int index, Node v)
    {
        nodes[index] = v;
    }

    //边的数目属性 
    public int NumEdges
    {
        get
        {
            return numEdges;
        }
        set
        {
            numEdges = value;
        }
    }

    //获取matrix[index1, index2]的值
    public int GetMatrix(int index1, int index2)
    {
        return matrix[index1, index2];
    }

    //设置matrix[index1, index2]的值 
    public void SetMatrix(int index1, int index2, int v)
    {
        matrix[index1, index2] = v;
    }

    //获取顶点的数目 
    public int GetNumOfVertex()
    {
        return nodes.Length;
    }

    //获取边的数目 
    public int GetNumOfEdge()
    {
        return numEdges;
    }

    //v是否是无向网的顶点 
    public bool IsNode(Node v)
    {
        //遍历顶点数组 
        foreach (Node nd in nodes)
        {
            //如果顶点nd与v相等，则v是图的顶点，返回true 
            if (v.Equals(nd))
            {
                return true;
            }
        }

        return false;
    }

    //获得顶点v在顶点数组中的索引 
    public int GetIndex(Node v)
    {
        int i = -1;

        //遍历顶点数组 
        for (i = 0; i < nodes.Length; ++i)
        {
            //如果顶点nd与v相等，则v是图的顶点，返回索引值 
            if (nodes[i].Equals(v))
            {
                return i;
            }
        }
        return i;
    }

    //在顶点v1、v2之间添加权值为v的边 
    public void SetEdge(Node v1, Node v2, int v)
    {
        //v1或v2不是无向网的顶点 
        if (!IsNode(v1) || !IsNode(v2))
        {
            Debug.WriteLine("Node is not belong to Graph!"); return;
        }

        //矩阵是对称矩阵 
        matrix[GetIndex(v1), GetIndex(v2)] = v;
        matrix[GetIndex(v2), GetIndex(v1)] = v;
        ++numEdges;
    }

    //删除v1和v2之间的边 
    public void DelEdge(Node v1, Node v2)
    {
        //v1或v2不是无向网的顶点 
        if (!IsNode(v1) || !IsNode(v2))
        {
            Debug.WriteLine("Node is not belong to Graph!"); return;
        }

        //v1和v2之间存在边 
        if (matrix[GetIndex(v1), GetIndex(v2)] != int.MaxValue)
        {
            //矩阵是对称矩阵 
            matrix[GetIndex(v1), GetIndex(v2)] = int.MaxValue;
            matrix[GetIndex(v2), GetIndex(v1)] = int.MaxValue;
            --numEdges;
        }
    }

    //判断v1和v2之间是否存在边 
    public bool IsEdge(Node v1, Node v2)
    {
        //v1或v2不是无向网的顶点 
        if (!IsNode(v1) || !IsNode(v2))
        {
            Debug.WriteLine("Node is not belong to Graph!");
            return false;
        }

        //v1和v2之间存在边 
        if (matrix[GetIndex(v1), GetIndex(v2)] != int.MaxValue)
        {
            return true;
        }
        else  //v1和v2之间不存在边 
        {
            return false;
        }
    }
}

为实现普里姆算法，需要设置两个辅助一维数组 lowcost 和 closevex，lowcost 用来保存集合 V-U 中各顶点与集合 U 中各顶点构成的边中具有小权值的边的 权值；closevex 用来保存依附于该边的在集合 U 中的顶点。假设初始状态时， U={u1}（u1 为出发的顶点），这时有 lowcost[0]=0，它表示顶点 u1 已加入集合 U 中。数组 lowcost 元素的值是顶点 u1 到其他顶点所构成的直接边的权值。然后 不断选取权值小的边(ui,uk)(ui∈U,uk∈V-U)，每选取一条边，就将 lowcost[k] 置为 0，表示顶点 uk 已加入集合 U 中。由于顶点 uk 从集合 V-U 进入集合 U 后， 这两个集合的内容发生了变化，就需要依据具体情况更新数组lowcost和closevex 中部分元素的值。把普里姆算法 Prim 作为 NetAdjMatrix类的成员方法。 

普里姆算法 Prim 的实现如下： 

 public int[] Prim()
    {
        int[] lowcost = new int[nodes.Length];   //权值数组 
        int[] closevex = new int[nodes.Length];  //顶点数组
        int mincost = int.MaxValue;              // 小权值 

        //辅助数组初始化 
        for (int i = 1; i < nodes.Length; ++i)
        {
            lowcost[i] = matrix[0, i]; closevex[i] = 0;
        }

        //某个顶点加入集合U 
        lowcost[0] = 0; closevex[0] = 0; for (int i = 0; i < nodes.Length; ++i)
        {
            int k = 1; int j = 1;

            //选取权值 小的边和相应的顶点 
            while (j < nodes.Length)
            {
                if (lowcost[j] < mincost && lowcost[j] != 0)
                {
                    k = j;
                }
                ++j;
            }

            //新顶点加入集合U 
            lowcost[k] = 0;

            //重新计算该顶点到其余顶点的边的权值 
            for (j = 1; j < nodes.Length; ++j)
            {
                if (matrix[k, j] < lowcost[j])
                {
                    lowcost[j] = matrix[k, j]; closevex[j] = k;
                }
            }
        }

        return closevex;
    }

表 6.1 给出了在用普里姆算法构造图 6.15(a)的小生成树的过程中数组 closevex 和 lowcost 及集合 U，V-U 的变化情况，读者可进一步加深对普里姆算 法的理解。

在普里姆算法中，第一个for循环的执行次数为n-1，第二个for循环中又包括 了一个while循环和一个for循环，执行次数为 2(n-1)2，所以普里姆算法的时间复 杂度为。

表 6.1     在用普里姆算法构造图 6.15(a)的 小生成树的过程中参数变化

顶点	i=0	1	2	3	4
	low      close cost       vex	low      close cost     vex	low      close cost    vex	low     close cost      vex	low     close cost     vex
A	0         0	0         3	0     3	0        3	0         3
B	60       0	60        0	60    0	0         0	0         0
C	100    0	100       0	70    4	70        4	0         4
D	20      0	0         0	0     0	0         0	0        0
E	∞       0	10        3	0     3	0         3	0         3
U	A	A,D	A,D,E	A,D,E,B	A,D,E,B,C
V-U	B,C,D,E	B,C,E	B,C	C
T	{}	{(A,D)}	{(A,D) (D,E)}	{(A,D) (D,E) (A,B)}	{(A,D) (D,E) (A,B) (E,C)}

 3、克鲁斯卡尔(Kruskal)算法 

克鲁斯卡尔算法的基本思想是：对一个有 n 个顶点的无向连通网，将图中的 边按权值大小依次选取，若选取的边使生成树不形成回路，则把它加入到树中； 若形成回路，则将它舍弃。如此进行下去，直到树中包含有 n-1 条边为止。 

【例 6-4】以图 6.2(a)为例说明用克鲁斯卡尔算法求无向连通网小生成树 的过程。 

第一步：首先比较网中所有边的权值，找到小的权值的边(D,E)，加入到 生成树的边集 TE 中，TE={(D,E)}。

第二步：再比较图中除边(D,E)的边的权值，又找到小权值的边(A,D)并且 不会形成回路，加入到生成树的边集 TE 中，TE={(A,D),(D,E)}。

第三步：再比较图中除 TE 以外的所有边的权值，找到小的权值的边(A,B) 并且不会形成回路，加入到生成树的边集 TE 中，TE={(A,D),(D,E),(A,B)}。

第四步：再比较图中除 TE 以外的所有边的权值，找到小的权值的边(E,C) 并且不会形成回路，加入到生成树的边集 TE 中，TE={(A,D),(D,E),(A,B),(E,C)}。

此时，边集 TE 中已经有 n-1 条边，所以求图 6.15(a)的无向连通网的小生 成树的过程已经完成，如图 6.16 所示。这个结果与用普里姆算法得到的结果相 同。