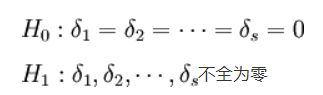数学建模、统计学之方差分析
概述
主要用于多组均数 之间的显著性检验。
如:
- 要推断这几种工艺制成的灯泡寿命是否有显著差异;
- 用几种化肥和几个小麦品种在若干块试验田里种植小麦,要推断不同的化肥和品种对产量有无显著影响。
上面提到的灯泡寿命问题是单因素试验,小麦产量问题是多因素试验。处理这些试验结果的统计方法就称为单因素方差分析和双因素方差分析。
这种用数理统计分析试验结果、鉴别各因素对结果影响程度的方法称为方差分析(Analysis Of ariance),记作 ANOVA。
人们关心的试验结果称为指标,试验中需要考察、可以控制的条件称为因素或因子,因素所处的状态或数量等级称为水平。

前提
- 正态性:每组样本数据对应的总体应该服从正态分布;
- 方差齐性: 每组样本数据对应的总体方差要相等,方差相等又叫方差齐性;
- 独立性随机性:每组之间的值是相互独立的,随机的,就是各个组的值不会相互影响。
实验设计三原则
- 重复
- 重复是指试验中同- -处理实施在两个或两个以上的试验单位上
- 随机化
- 随机化是指在对实验对象进行分组时必须使用随机的方法,使对象进入各实验组的机会相等,以避免试验对象分组时实验人员主观倾向的影响
- 局部控制——实验条件的局部一致性
- 在实验环境或实验单位差异大的情况下,可将整个实验环境或实验单位分成若千个小环境或小组,在小环境或小组内使非处理因素尽量一致,这就是局部控制
单因素方差分析
只考虑一个因素 A 对指标的影响, A 取几个水平,在每个水平上作若干个试验(为随机变量),试验过程中除 A 外其它影响指标的因素都保持不变(只有随机因素存在),我们的任务是从试验结果推断:当 A 取不同水平时指标有无显著差别,相当于检验若干总体的均值是否相等。
单因素方差分析基本步骤
- 提出原假设:H0——无差异;H1——有显著差异
- 选择检验统计量:方差分析采用的检验统计量是F统计量,即F值检验。
- 计算检验统计量的观测值和概率P值:该步骤的目的就是计算检验统计量的观测值和相应的概率P值。
- 给定显著性水平,并作出决策。
数学模型
如下表 A 1 — A r A_1—A_r A1—Ar是取了r个不同的水平, x r 1 — x r n 是 A r x_{r1}—x_{rn}是A_r xr1—xrn是Ar水平上的n个若干实验。 x r n x_{rn} xrn服从正态分布, x i − N ( μ i , σ 2 ) x_i - N( \mu_i, \sigma^2) xi−N(μi,σ2),

将第i 行称为第i 组数据。判断 A 的 r 个水平对指标有无显著影响,相当于要作以
下的假设检验

由于 x i j x_{ij} xij 的取值既受不同水平 A i A_i Ai 的影响,又受 A i A_i Ai固定下随机因素的影响,所以将它分解为
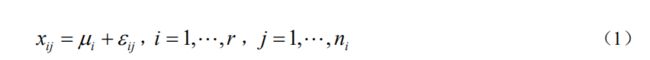
其中 ε i j − N ( 0 , σ 2 ) ε_{ij}- N(0,σ^2) εij−N(0,σ2) ,且相互独立。记
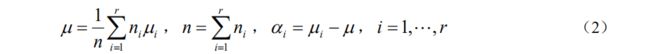
μ 是总均值, α i α_i αi 是水平 A i A_i Ai对指标的效应。由(1)、(2)模型可表为
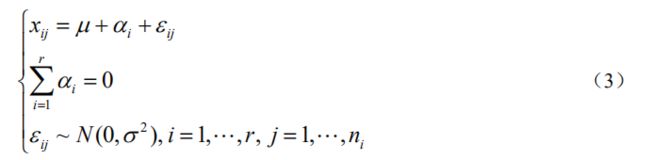
统计分析

经分解可得:

记

则 S T = S A + S E S_T=S_A+S_E ST=SA+SE
S A S_A SA是各组均值对总方差的偏差平方和,称为组间平方和; S E S_E SE 是各组内的数据对均值偏差平方和的总和。 S A S_A SA反映 A 不同水平间的差异, S E S_E SE 则表示在同一水平下随机误差的大小。
往下看的有点懵逼了,直接复制原文了、、、
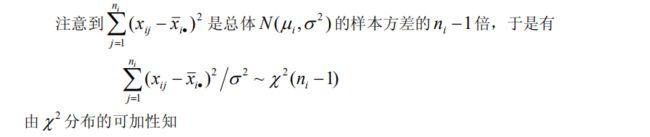
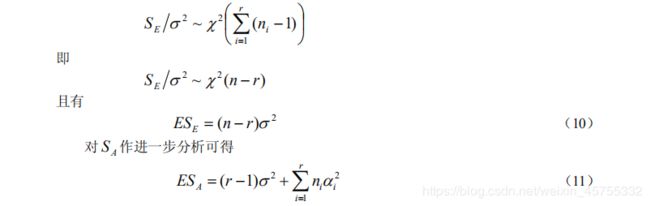


方差分析表

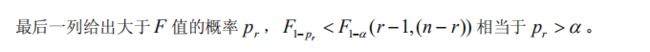
方差分析一般用的显著性水平是:取α = 0.01,拒绝 H0 ,称因素 A 的影响(或 A
各水平的差异)非常显著;取α = 0.01,不拒绝 H0 ,但取α = 0.05 ,拒绝 H0 ,称因
素 A 的影响显著;取α = 0.05 ,不拒绝 H0 ,称因素 A 无显著影响。
Matlab 实现
若各组数据个数相等,称为均衡数据。若各组数据个数不等,称非均衡数据
均衡数据
用p=anoval(x)处理均衡数据
返回值 p 是一个概率,当 p > α 时接受 H0 ,x 为m× r 的数据矩阵,x 的每一列是一个水平的数据(这里各个水平上的样本容量 n i = m n_i = m ni=m )。另外,还输出一个方差表和一个Box 图。
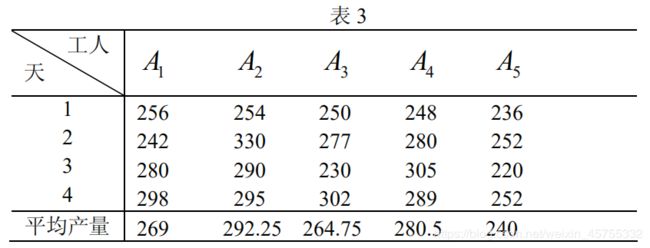
例1 为考察 5 名工人的劳动生产率是否相同,记录了每人 4 天的产量,并算出其平均值,如表3 。你能从这些数据推断出他们的生产率有无显著差别吗?
MATLAB中的anova1()函数单因素方差分析
解 编写程序如下:
x=[256 254 250 248 236
242 330 277 280 252
280 290 230 305 220
298 295 302 289 252];
p=anova1(x)
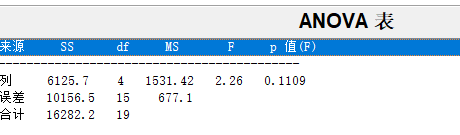
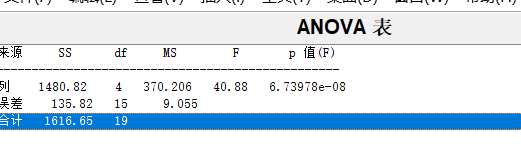
MS是均方误差,即每个变异源的SS/df
f 统计量是均方误差的比值
p值是测试统计量取的值大于计算的测试统计量的值的概率
求得p=0.1109>a=0.05,故接受H0,即5名工人的生产率没有显著差异。
非均衡数据
处理非均衡数据的用法为:
p=anova1(x,group)
x为向量,从第 1 组到第 r 组数据依次排列;group 为与 x 同长度的向量,标志 x 中数据的组别(在与 x 第i 组数据相对应的位置处输入整数i(i=1,2…,r))。
例 2 用 4 种工艺生产灯泡,从各种工艺制成的灯泡中各抽出了若干个测量其寿命,结果如下表,试推断这几种工艺制成的灯泡寿命是否有显著差异。
MATLAB中的 anova1()函数单因素方差分析

x=[1620 1580 1460 1500
1670 1600 1540 1550
1700 1640 1620 1610
1750 1720 1680 1800];
x=[x(1:4),x(16),x(5:8),x(9:11),x(12:15)];
g=[ones(1,5),2*ones(1,4),3*ones(1,3),4*ones(1,4)];
p=anova1(x,g)
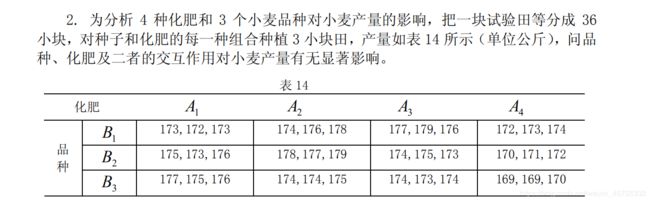
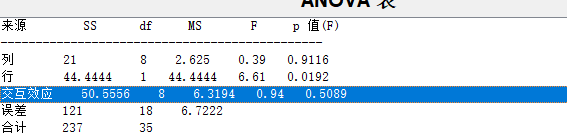
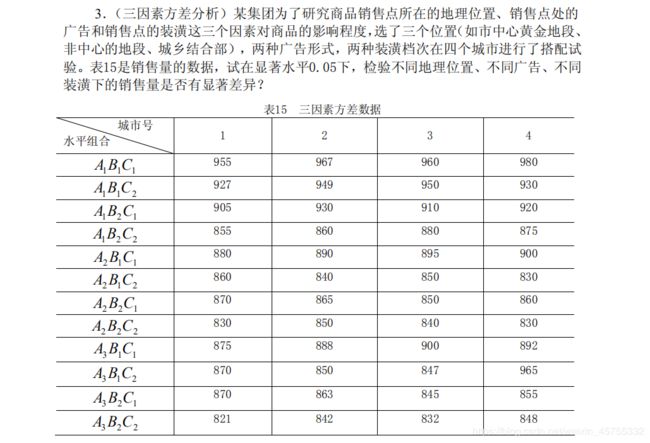
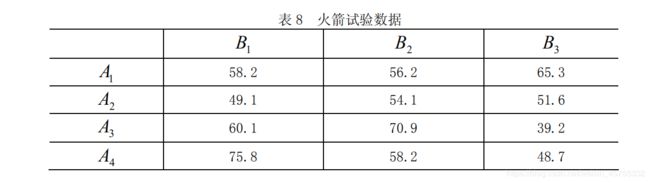
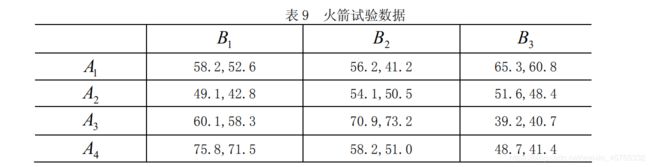
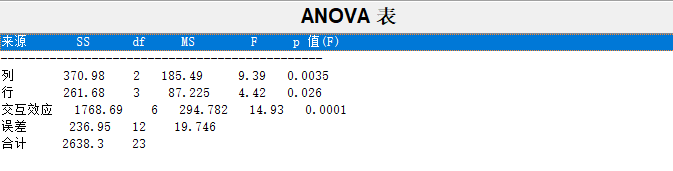
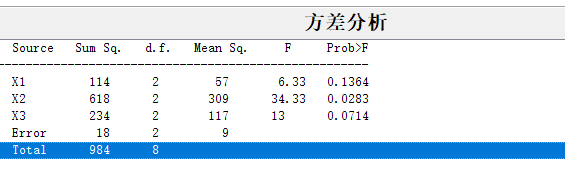
求得 0.01 若我们想知道某个组与另外其他组有无显著性差异,可以这样做 表没有啥变化 单因素就是只考虑一个因素,探讨该因素的改变对我们最终结果有无显著差异。其具体推导过程,我看到一半看不懂了,以后看懂了再具体写吧。但一定要会应用,MATLAB挺方便的,当然会spss更方便。 如果要考虑两个因素 A,B 对指标的影响, A,B 各划分几个水平,对每一个水平组合作若干次试验,对所得数据进行方差分析,检验两因素是否分别对指标有显著影响,或者还要进一步检验两因素是否对指标有显著的交互影响。 一种火箭使用了四种燃料、三种推进器,进行射程试验,对于每种燃料与每种推进器的组合作一次试验,得到试验数据如表 8。问各种燃料之间及各种推进器之间有无显著差异? 记燃料为因素 A ,它有 4 个水平,水平效应为αi ,i = 1,2,3,4 。推进器为因素 B ,它有 3 个水平,水平效应为 β j , j =1,2,3。我们在显著性水平α = 0.05 下检验。 一火箭使用了 4 种燃料,3 种推进器作射程试验,每种燃料与每种推进器的组合各发射火箭 2 次,得到如表 9 结果。 求得 p=0.0035 、0.0260、 0.0001,表明各试验均值相等的概率都为小概率,故可拒绝均值相等假设。即认为不同燃料(因素 A )、不同推进器(因素 B )下的射程有显著差异,交互作用也是显著的。6 由于因素较少,我们可以对不同因素的所有可能的水平组合做试验,这叫做全面试验。 最简单的正交表是 L 4 ( 2 3 ) L4(2^3) L4(23),含意如下:“L”代表正交表;L 下角的数字“4”表示有 4 横行,简称行,即要做四次试验;括号内的指数“3”表示有3 纵列,简称列,即最多允许安排的因素是3 个;括号内的数“2”表示表的主要部分只有2 种数字,即因素有两种水平1与2。正交表的特点是其安排的试验方法具有均衡搭配特性。 为提高某种化学产品的转化率(%),考虑三个有关因素:反应温度 A(℃),反应时间 B(min)和使用催化剂的含量C(%)。各因素选取三个水平,如表 11 所示 求得概率 p= 0.1364、0.0283 、0.0714,可见因素 B、C 的各水平对指标值的影响有显著差异(显著性水平取 0.1),而因素 A 的各水平对指标值的影响无显著差异。 可以看到,每一行代表一个品种,列是化肥,再看下面p值,可以得出结论,品种对小麦产量有显著影响,化肥和两者的交互作用没有显著影响x=[1620 1580 1460 1500
1670 1600 1540 1550
1700 1640 1620 1610
1750 1720 1680 1800];
x=[x(1:4),x(16),x(5:8),x(9:11),x(12:15)];
g=[ones(1,5),2*ones(1,4),3*ones(1,3),4*ones(1,4)];
[p,t,st]=anova1(x,g)
[c,m,h,nms] = multcompare(st);
[nms num2cell(m)]
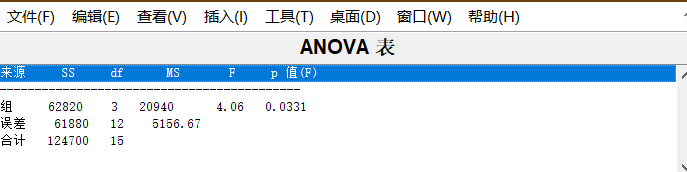
点击一下这几条直线,就可以找出直线对应的组,下面出现与哪个组有差异。
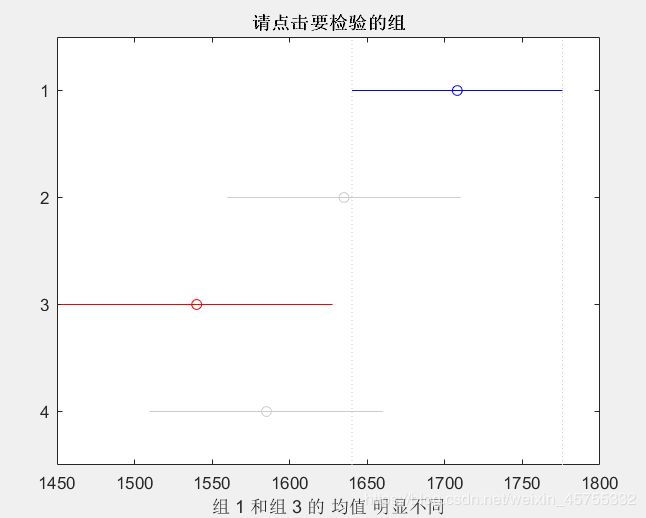
总结
双因素方差分析
推导不推了,自己没看懂。。。

直接看例题应用吧例 3
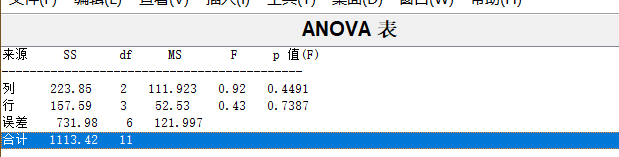
求得p=0.4491和0.7387,表明各种燃料和各种推进器之间的差异对于火箭射
程无显著影响。例 4
clc,clear
x0=[58.2,52.6 56.2,41.2 65.3,60.8
49.1,42.8 54.1,50.5 51.6,48.4
60.1,58.3 70.9,73.2 39.2,40.7
75.8,71.5 58.2,51.0 48.7,41.4];
x1=x0(:,1:2:5);x2=x0(:,2:2:6);
for i=1:4
x(2*i-1,:)=x1(i,:);
x(2*i,:)=x2(i,:);
end
[p,t,st]=anova2(x,2)
正交试验设计与方差分析
当因素较多时,虽然理论上仍可采用前面的方法进行全面试验后再做相应的方差分析,但是在实际中有时会遇到试验次数太多的问题。于是我们考虑是否可以选择其中一部分组合进行试验,这就要用到试验设计方法选择合理的试验方案,使得试验次数不多,但也能得到比较满意的结果。用正交表安排试验
当然正交表有很多,剩余的可以看这里
例题
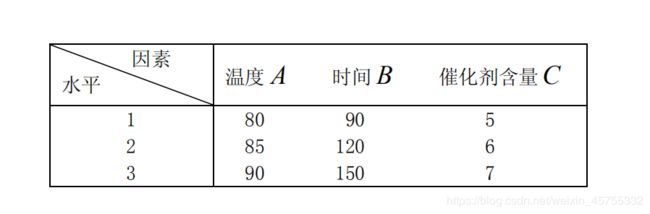
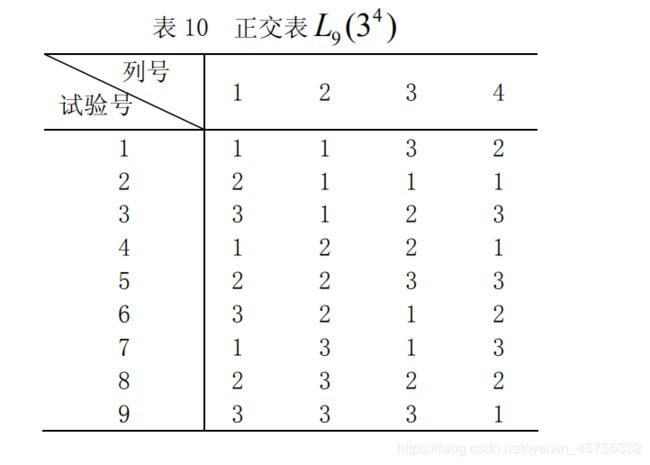
如果做全面试验,则需 3 3 = 27 3^3=27 33=27次,若用正交表 L 9 ( 3 4 ) L9(3^4) L9(34),仅做 9 次试验。将三个因素 A, B,C 分别放在 L 9 ( 3 4 ) L9(3^4) L9(34) 表的任意三列上,如将 A, B 分别放在 L 9 ( 3 4 ) L9(3^4) L9(34)第 1,2 列上,C 放在 L 9 ( 3 4 ) L9(3^4) L9(34)的第 4 列上。将表中 A, B,C 所在的三列上的数字 1,2,3 分别用相应的因素水平去替代,得 9 次试验方案。以上工作称为表头设计。再将 9 次试验结果转化率数据列于表上(见表 12)。
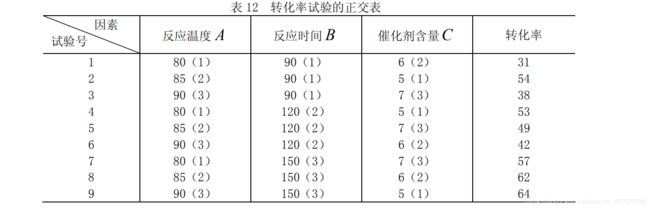
y=[31 54 38 53 49 42 57 62 64];
g1=[1 2 3 1 2 3 1 2 3];
g2=[1 1 1 2 2 2 3 3 3];
g3=[2 1 3 1 3 2 3 2 1];
[p,t,st]=anovan(y,{g1,g2,g3})
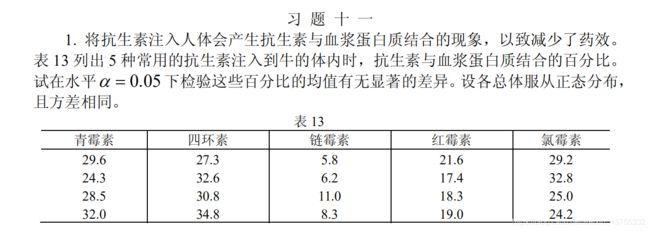
练习
y=[ 29.6 27.3 5.8 21.6 29.2
24.3 32.6 6.2 17.4 32.8
28.5 30.8 11 18.3 25
32 34.8 8.3 19 24.2];
anova1(y)
x=[173,172,173,175,173,176 ,177,175,176
174,176,178 ,178,177,179,174,174,175
177,179,176 ,174,175,173,174,173,174
172,173,174,170,171,172 ,169,169,170];
anova2(x,2)