机器学习：决策树

决策树是机器学习中非常基础的算法，也是我研究生生涯学习到的第一个有监督模型，其中最基础的ID3是1986年被发表出来的，一经发表，之后出现了众多决策树算法，不过最常见的还是C4.5和cart树。在我的研究中，用不到决策树，在天池或者Kaggle也很少用到单个决策树，这种竞赛一般用的集成算法较多，毕竟是20世纪的产物，经过这么多年的发展，已经有了很多可供选择的模型。其实很多基础模型都是如此，在研究中根本用不到，但是你得了解这些模型，下面我就根据我的了解来谈谈决策树。本文全部的代码都放在我的github。

引言

决策树的分类过程类似于小时候玩的那种性格测试题，就是不断地做选择题，然后跳到下一题继续做，直到最后出来结果。从中也可以看出它就是一个if-else决策过程，我做选择提供信息，它根据信息减少范围，更确切地就是消除不确定性，我提供的选择越多，提供的信息也就越多，那么不确定性就越小，它就越能测出我是哪种性格。根据数学之美里面的说法就是信息量就是不确定性的多少，最终我提供了大量信息，那么它也消除了不确定性，给出了结果。

小时候我做这种性格测试题的时候，思考过为什么这些题目就能测出？它测的难道真的就是对的吗？这些题目都是哪来的？现在想来，这些都是模型建立的问题，也就是用决策树来测数据之前，我们如何建立这个决策树。那这些题目的依据从何而来呢？我猜想是心理学家通过大量调查得到的，具体就是心理学家调查了很多人，这些信息多到可以总结出一个规律出来，这个规律就是人类性格的规律，如果这些题目给外星人做，那肯定就不行了，心理学家还需要先对大量外星人做问卷调查，然后得到大量信息做出适合外星人的题目。那我们建立关于某类数据的决策树的时候，也需要先得到大量的相关信息，这种相关信息在机器学习中被称为训练数据。但是我那时就想到如果心理学家调查那些人的时候，有些人为了捣乱专门回答相反的呢？这些人的回答肯定不能用，有些人可能为了保护隐私不能回答一些比较私人的问题呢？，并且每个人都有特别之处，心理学家不能把所有人都包括进去，心理学家需要找出的是大部分人的特征即可。那么在我们使用的训练数据中也有这样的情况，这是因为现实数据往往很复杂，也有可能缺失值，也有个别特殊情况，我们也不需要决策树模型将这些数据全部学习，但是决策树模型是死的，它并不会像心理学家一样挑选数据，它只会全部学习完，这种情况在机器学习中就叫做过拟合，这种问题在大型网络模型中特别常见，需要做的减少特殊情况，适用一般情况，专业话就是提高泛化能力。那么心理学家如何才能得到大部分的人心理答案呢？最简单的就是减少设置的题目，这样问的就不是那么细了，只问笼统的问题，这样出来的结果就会好一点。到决策树中就是剪枝策略，减去一些没用的属性，只保留对模型有用的属性分支，这也符合了奥卡姆剃刀原理，越精简越好。

这就是所有模型所都要考虑的：

1. 如何建立模型？
2. 如何处理数据？
3. 如何精简模型？

熵

决策树就是根据信息减少不确定性，那么正如上面所说，心理学家会减少设置的题目，那么如何知道每一道题目都提供了多少信息量呢，那我们需要的就是根据得到的数据度量信息，我们可以从生活中来看信息量等于什么，当我们对一件事很了解的时候，那么我们需要的信息就少，我们对一件事不了解，那么需要的信息就多，那么我们对一件事完全了解所需要的信息量就是不确定性的多少，将得到的信息填满这个不确定，就变成了确定。那么如何量化这种度量方式呢，也就是如何用公式表示出来？数学之美这本书给出了一个非常好的例子，就是我错过看世界杯，但是我想知道冠军是谁，就问一位观众，但是这个人不肯告诉我，只是说让我猜，他收钱之后告诉我，我猜的对不对，那么我要花多少钱才能在32中球队中猜中呢？我也是个程序员了，自然知道二分查找，分别给球队编上号，问他，冠军球队是否在1-16中，他说对的，我接着说，冠军球队是否在1-8中，他说错了，那么我也知道冠军球队在9-16中，这样猜的话，只需要五次就能猜出，那么谁是冠军这个消息只值五块钱，我们知道\(log32 = 5\)，正好二者对应起来，他就是个对数函数。

上面的猜测是基于概率相等的情况，但是球迷都知道有强队，有弱队，冠军很有可能就是在强队中出现的，因而每个队都有自身的夺冠概率，这样的话就不能直接用\(log32 = 5\)来计算，需要用概率来计算，那么可以将\(log32 = 5\)直接进行拆分就可以，将之变成\(log32 = -(\frac{1}{32}log\frac{1}{32} + \frac{1}{32}log\frac{1}{32} + \dots + \frac{1}{32}log\frac{1}{32})\)，那么当大家概率都不同的时候，它的准确信息量就是\(H = -(p_1logp_1 + p_2logp_2 + \dots + p_{32}logp_{32})\)，香农称之为信息熵(Entropy)，衡量了系统的不确定性，如果要消除不确定性，所要付出的最小努力大小就是这个信息熵\(-\sum\limits_{i=1}^{32}p_klog{p_k}\)。而上面概率都相等的情况，也被称为最大熵，也被用于最大熵模型中。现在有了每只球队的夺冠真实概率，但是如果我是个伪球迷，我凭感觉猜每个球队的夺冠概率分别是\(q_k\)，然后将之用到\(\sum\limits_{i=1}^{32}p_klog\frac{1}{q_k}\)，这个就是交叉熵，给定真实分布的情况下，使用非真实分布指定的策略消除不确定性所作出的努力，交叉熵一般用作损失函数，交叉熵越低，越好。最后我发现我猜的都是错的，我想要衡量一下我们之间猜的差异，也就是衡量俩个分布之间的差异，用的就是相对熵，也就是推导SVM中的KL散度，它的公式就是交叉熵减去信息熵\(KL(p|q) = \sum\limits_{i=1}^{32}p_klog\frac{1}{q_k} - \sum\limits_{i=1}^{32}p_klog\frac{1}{p_k}\)。这些熵之后都会使用到。借此机会正好全部分析好。

ID3

理论分析

如果目前已经有了大量的训练数据D，那么我们只要从这些数据中依次挑选出数据特征(数据属性)来作为决策树的结点，那么哪一个特征具有最强的分类能力呢？从上面的熵可知，最好的特征会使得分类的不确定性下降到最低，计算的也就是由于特征A使得对训练数据分类的不确定性减少的程度，专业话就是信息增益，那么我们需要计算的就是本身的不确定性和在特征A下分类的不确定性，使用\(本身的不确定性 - 在特征A下分类的不确定性 = 不确定性减少的程度\)，机器学习中将之称为信息增益，这个公式专业化就是\(信息熵 - 条件熵 = 信息增益\)

\[Gain(D,A) = H(D) - H(D|A) \]

\[H(D|A) = \sum\limits_{v = 1}^{V}\frac{|D^v|}{|D|}H(D^v) \]

条件熵中的\(v\)就是特征A中的离散值，离散值就是不能无限细分的，比如性别，只有男和女俩个值，对于连续值的特征的选择，之后我们会讲。那么我们就可以利用上面得到的信息增益来进行特征选择，选择信息增益最大的作为该节点，该特征的离散值作为该节点的分支，之后在每个分支下，仅仅使用该节点下的数据集来计算信息熵和剩下的每个特征的条件熵，继续进行特征选择，直到停止条件：1. 当前节点所包含的样本都是同一类的，无需划分；2. 已经选完了全部的属性了，无法划分了；3. 当前节点包含的数据集为空，没有数据了，不能划分。空谈误国，实业兴邦，下面以李航博士的统计学习方法一书中的一个列子，依托上面的过程来做一下，真正的计算一下才能加深理解。

ID	年龄	有工作	有自己房子	信贷情况	类别
1	青年	否	否	一般	否
2	青年	否	否	好	否
3	青年	是	否	好	是
4	青年	是	是	一般	是
5	青年	否	否	一般	否
6	中年	否	否	一般	否
7	中年	否	否	好	否
8	中年	是	是	好	是
9	中年	否	是	非常好	是
10	中年	否	是	非常好	是
11	老年	否	是	非常好	是
12	老年	否	是	好	是
13	老年	是	否	好	是
14	老年	是	否	非常好	是
15	老年	否	否	一般	否

先计算整体的信息熵，直接看类别一列，发现类别为否的概率是\(\frac{6}{15}\)，类别为是的概率是\(\frac{9}{15}\)，利用公式计算整体信息熵

\[H(D) =-(\frac{6}{15}log\frac{6}{15} + \frac{9}{15}log\frac{9}{15}) = 0.97 \]

之后再计算每个特征下的条件熵，要想计算每个特征的条件熵，先计算这个特征中每个离散值的信息熵。

\[H(年龄 = 青年) = -(\frac{2}{5}log\frac{2}{5} + \frac{3}{5}log\frac{3}{5}) = 0.97 \]

\[H(年龄 = 中年) = -(\frac{3}{5}log\frac{3}{5} + \frac{2}{5}log\frac{2}{5}) = 0.97 \]

\[H(年龄 = 老年) = -(\frac{4}{5}log\frac{4}{5} + \frac{1}{5}log\frac{1}{5}) = 0.72 \]

用每个离散值的信息熵乘以个数比例就是条件熵。

\[H(D|年龄) = \frac{1}{3}H(年龄 = 青年) + \frac{1}{3}H(年龄 = 中年) + \frac{1}{3}H(年龄 = 老年)=0.888 \]

\[Gain(D,年龄) = H(D) - H(D|年龄) = 0.97 - 0.888 = 0.083 \]

之后每个都像上面那个计算，计算有工作的特征的信息增益

\[Gain(D,有工作) = H(D) - H(D|有工作) = 0.97 - (\frac{1}{3}H(有工作 = 是) + \frac{2}{3}H(有工作 = 否)) \]

\[Gain(D,有工作) = 0.97 - (\frac{1}{3}\times0+ \frac{2}{3}(-\frac{4}{10}log\frac{4}{10}-\frac{6}{10}log\frac{6}{10}) = 0.32 \]

计算有自己房子的信息增益

\[Gain(D,有自己房子) = H(D) - H(D|有自己房子) = 0.97 - (\frac{6}{15}H(有自己房子 = 是) + \frac{9}{15}H(有自己房子 = 否)) \]

\[Gain(D,有自己房子) = 0.97 - (\frac{2}{5}\times0+ \frac{3}{5}(-\frac{3}{9}log\frac{3}{9}-\frac{6}{9}log\frac{6}{9}) = 0.42 \]

计算信贷情况的信息增益

\[Gain(D,信贷情况) = H(D) - H(D|信贷情况) = 0.97 - (\frac{5}{15}H(信贷情况 = 一般) + \frac{6}{15}H(信贷情况 = 好) + \frac{4}{15}H(信贷情况 = 非常好)) \]

\[Gain(D,信贷情况) = 0.97 - (\frac{1}{3}(-\frac{4}{5}log\frac{4}{5} - \frac{1}{5}log\frac{1}{5})+ \frac{2}{5}(-\frac{2}{6}log\frac{2}{6}-\frac{4}{6}log\frac{4}{6}) + \frac{4}{15}\times0) = 0.37 \]

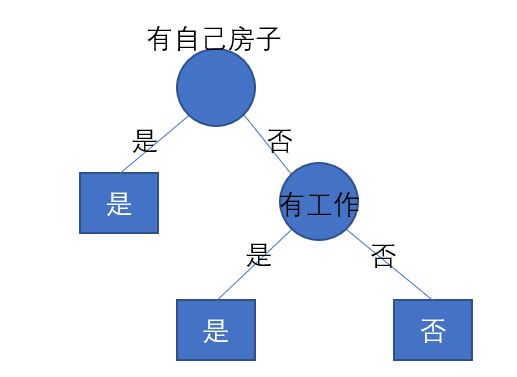
找出信息增益最大的那个作为决策树的第一个节点，也就是特征(有自己的房子)作为第一个节点，是和否作为节点左右分支，删除数据集D中有自己房子这一特征，并将是和否俩个分支的数据集分别划分出来，否的数据如下所示

ID	年龄	有工作	信贷情况	类别
1	青年	否	一般	否
2	青年	否	好	否
3	青年	是	好	是
4	青年	否	一般	否
5	中年	否	一般	否
6	中年	否	好	否
7	老年	是	好	是
8	老年	是	非常好	是
9	老年	否	一般	否

从这些数据中再进行信息增益的计算，先计算整体的信息熵

\[H(D) =-(\frac{1}{3}log\frac{1}{3} + \frac{2}{3}log\frac{2}{3}) = 0.918 \]

计算年龄的信息增益

\[H(D|年龄) = 0.918 - (\frac{4}{9}H(D|年龄 = 青年) + \frac{2}{9}H(D|年龄 = 中年) + \frac{3}{9}H(D|年龄 = 老年)) \]

\[H(D|年龄) = 0.918 - (\frac{4}{9}(-\frac{1}{4}log\frac{1}{4} - \frac{3}{4}log\frac{3}{4})+ \frac{2}{9}\times0+ \frac{3}{9}(-\frac{1}{3}log\frac{1}{3} - \frac{2}{3}log\frac{2}{3})) = 0.918 - 0.666 = 0.252 \]

计算有工作的信息增益

\[H(D|有工作) = 0.918 - (\frac{3}{9}H(D|有工作 = 是) + \frac{6}{9}H(D|有工作 = 否)) \]

\[H(D|有工作) = 0.918 - (\frac{3}{9}\times0+ \frac{6}{9}\times0) = 0.918 \]

计算信贷情况

\[H(D|信贷情况) = 0.918 - (\frac{4}{9}H(D|信贷情况 = 一般) + \frac{4}{9}H(D|信贷情况 = 好) + \frac{1}{9}H(D|信贷情况 = 非常好)) \]

\[H(D|信贷情况) = 0.918 - (\frac{4}{9}\times0 + \frac{4}{9}(-\frac{1}{2}log\frac{1}{2} - \frac{1}{2}log\frac{1}{2}) + \frac{1}{9}\times0) = 0.918 - 0.444 = 0.474 \]

直接选出特征(有工作)，并且它的俩边数据集都是属于同一类别，无需再划分了。
特征(有自己房子 = 是)数据如下所示

ID	年龄	有工作	有自己房子	信贷情况	类别
1	青年	是	是	一般	是
2	中年	是	是	好	是
3	中年	否	是	非常好	是
4	中年	否	是	非常好	是
5	老年	否	是	非常好	是
6	老年	否	是	好	是

发现都是属于同一类别的，那么就不用计算了，根据上面的过程ID3就生成了

代码实现

这节我们根据上面的过程写代码，首先看树如何存储，这次的树非常简单，因此我们使用字典来存储即可，对于决策树的建立，根据之前的数据结构中内容，我们使用递归建树，先看递归结束条件，之后开始进行特征选择，然后从数据中删除该特征，然后开始建立决策树。

#递归建树
def buildTree(dataSet,labelSet):
    decision = [example[-1] for example in dataSet]
    decisionType = set(decision)
    #如果熵值为0
    if len(decisionType) == 1:
        return decisionType
    
    #这里的树采用了字典，二叉树的话，之后再实现
    #特征选择
    key = chioceBest(dataSet)
    keyLabel = labelSet[key]
    #构造决策树
    myTree = {keyLabel:{}}
    #使用完了就删除
    del labelSet[key]
    bestCol = [example[key] for example in dataSet]
    valueCol = set(bestCol)
    for value in valueCol:
        subLabel = labelSet[:]
        myTree[keyLabel][value] = buildTree(splitValue(dataSet,key,value),subLabel)
    return myTree

其中特征选择的代码也是和之前过程差不多，就是计算每个特征的信息增益，这里的话，其中不用计算整体熵值，因为整体熵值是一样的，我们只需要计算条件熵，看谁的条件熵最小即可。

#选择出最好的属性
def chioceBest(dataSet,entro = entropy):
    #计算出整个的熵值
    score_all = entropy(dataSet)
    print('整体信息熵', score_all)
    #最好的特征
    bestAttri = -1  
    #最好特征的增益因子
    bestAttriGain = 0.0
    #属性的个数
    attributes = len(dataSet[0]) - 1
    #计算每个属性的条件熵，并选出最好的那个
    for col in range(attributes):
        #得到这个列的所有的值
        data_col = [example[col] for example in dataSet]
        #得出这一属性的值
        values_col = set(data_col)
        col_entropy = 0.0
        #属性值的条件熵
        for value in values_col:
            #得出相关属性值的所有行数
            value_dataSet = splitValue(dataSet,col,value)
            newEntropy = entropy(value_dataSet)
            print('信息熵', newEntropy)
            ratio = len(value_dataSet)/len(dataSet) 
            col_entropy += ratio*newEntropy
        #得到增益因子   
        attributeGain = score_all - col_entropy
        print('信息增益:', attributeGain)
        if attributeGain > bestAttriGain:
            bestAttriGain = attributeGain
            bestAttri = col
    return bestAttri

之后将信息熵进行实现

#求一个属性值的信息熵
def entropy(rows):
    gainFactor = 0
    length = len(rows);
    #求出一个属性值的每个决策的数目
    decisionChoice = entropyDecision(rows)
    #对这个属性值求出熵值    
    for value in decisionChoice.keys():
        ratio = float(decisionChoice[value])/length
        gainFactor -= ratio*(math.log(ratio)/math.log(2))
    return gainFactor

C4.5

ID3的问题

问题1：上述处理的都是离散值，无法处理连续值。
问题2：信息增益在选择特征上会选择取值比较多的特征，这也是很容易理解，取值比较多的话，每个分支都是一个特征值，那么它更容易使数据变得更纯。也可以从公式来看，每个分支都是一个值，那么它的条件熵就是0，比如上面的特征ID。
问题3：对有缺失值的数据没有处理。
问题4：容易过拟合，没有考虑过拟合。

解决

问题1的解决，因为很多数据的特征都是连续值，因而必须要考虑到。这里我们可以使用二分法对连续属性离散化，具体做法就是先将全部特征值进行从小到大排序，之后俩点之间的中位点\(\frac{A^i + A^{i+1}}{2}\)作为候选划分点，然后像前面那样计算所有候选划分点的信息增益，选出信息增益最大的那个候选划分点，这个划分点就不再是特征值中的一员了，而是一个具体的数字。下面我们来算一个连续特征的信息增益看看，例子选自周志华的西瓜书。
假设西瓜数据集中有一个特征是密度，一共有17个西瓜，密度值分别

编号	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
密度	0.697	0.774	0.634	0.608	0.556	0.403	0.481	0.437	0.666	0.243	0.245	0.343	0.639	0.657	0.360	0.593	0.719
好瓜	是	是	是	是	是	是	是	是	否	否	否	否	否	否	否	否	否

1. 先将密度值进行从小到大排序，变成{0.243，0.245，0.343，0.360，0.403，0.437，0.481，0.556，0.593，0.608，0.634，0.639，0.657，0.666，0.697，0.719，0.774}。
2. 之后求俩俩中位数作为候选划分点，\(\frac{0.243 + 0.245}{2} = 0.244\)，如此一直计算，最终得到所有的候选划分点{0.244，0.294，0.351，0.381，0.420，0.459，0.518，0.574，0.600，0.621，0.636，0.648，0.661，0.681，0.708，0.746}。
3. 依次选取候选划分点，并且计算信息增益，比如，在此之前先计算整体

\[H(A) = -(\frac{8}{17}log\frac{8}{17} + \frac{9}{17}log\frac{9}{17}) = 0.998 \]

第一次选取0.244，那么小于0.244的只有0.243，大于0.244的有16个，分别计算。

\[H(D^-) = -(0\times log0 + 1\times\log1) = 0 \]

\[H(D^+) = -(\frac{8}{16}log\frac{8}{16} + \frac{8}{16}log\frac{8}{16}) = 1 \]

\[Gain(D，t=0.244) = 0.998 - (\frac{1}{17} + \frac{16}{17}) = 0.057 \]

然后选取0.294，再进行计算，一直计算下去。
4. 从上面的候选划分点中选取一个信息增益最大的，在这个例子中选取的是0.381，它的信息增益是0.262。

#连续数值候选的集合
def continuousCandidate(continuousDataSet):
    splitSet = []
    for i in range(len(continuousDataSet) - 1):
        temp = (continuousDataSet[i] + continuousDataSet[i+1])/2
        splitSet.append(temp)
    return splitSet

#连续变量的划分点的选择
def chooesContinueDivision(dataSet,col):
    #得到这一列中所有的值
    data_col = [example[col] for example in dataSet]
    data_col.sort()
    #得出切分点的候选集
    splitSet = continuousCandidate(data_col)
    #最好的切分点
    best_split = 0.0
    best_gain = 1000.0
    best_sets = None
    #选取信息增益最大的那个切分点
    for split in splitSet:
        leftPoint = []
        rightPoint = []
        for i in range(len(data_col)):
            if split >= dataSet[i][col]:
                leftPoint.append(dataSet[i])
            else:
                rightPoint.append(dataSet[i])
        left_gain = entropy(leftPoint)
        right_gain = entropy(rightPoint)
        gain = left_gain + right_gain
        if gain < best_gain:
            best_gain = gain
            best_split = split
            best_sets = [leftPoint,rightPoint]
    return best_gain,best_split,best_sets

问题2的解决，就是将信息增益变成信息增益率，C4.5并不是直接选择信息增益率，而是先用信息增益选出高于平均水平的属性，再从中选出信息增益率最高的。先来看看信息增益率，特征的特征值越多，信息增益就越大，那么可以想到，如果信息增益除以多特征值的相关表达式不就限制住了，这就是信息增益率的想法，因而可以定义为

\[GainRatio(D,A) = \frac{Gain(D,A)}{IV(A)} \]

其中

\[IV(A) = - \sum\limits_{v = 1}^{V}\frac{|D^v|}{|D|}log\frac{|D^v|}{|D|} \]

这个\(IV(A)\)式子中\(V\)取值越多的话，\(IV(A)\)的值就会越大。

问题3的解决，缺失值数据的处理，数据缺失在现实数据中很常用，但是我没有处理过这样的数据，我处理的都是天文光谱数据，这些数据都是经过天文台的处理，很少有缺失的数据，因而我对这部分只了解了大概。这方面一共有俩个问题

1. 如果训练数据有缺失值，那么如何进行特征选择？
2. 如果给定划分特征，数据有缺失值，如何进行样本的划分(这里不仅仅是测试数据，外加建立决策树选好特征，有缺失值的数据该划分到特征的哪个特征值中去)

这俩个问题都可以使用权重法，先给每个数据一个权重为\(\omega_i = 1\)，之后进行特征选择的时候，选出无该特征缺失值的数据\(D^w\)计算信息增益，计算出来的信息增益乘以权重\(\rho\)，这里的权重\(\rho\)就是无该特征缺失值的数据的总权重除以整个数据的总权重。

\[\rho = \frac{\sum_{i\in D^w} \omega_i}{\sum_{i\in D} \omega_i} \]

\[Gain(D，A) = \rho \times Gain(D^w，A) \]

依旧是选出信息增益最大的特征作为节点，之后将该节点缺失值的数据以不同的权重划分到全部分支中，这里的权重就是该分支无缺失值除以全部分支无缺失值，下图就是一个例子，假如数据8和10有缺失值，那么就以不同的权重进入三个分支中，其他的数据权重都是1，

这样就会影响分支中的信息增益权重\(\rho\)。

问题4的解决，引入正则化系数进行初步剪枝，一般都不会这样做，在CART树中有着更完善的剪枝策略。

CART

C4.5的问题

问题1：ID3和C4.5使用了信息熵，其中有了大量耗时的对数运算，如果连续值的话，还存在了排序，能够将之改进？
问题2：决策树算法非常容易过拟合，并且C4.5的剪枝算法也是需要优化的。思想就是俩种，预剪枝和后剪枝。
问题3：上面俩种都只能用于分类，能不能拓展到回归中？

CART树

CART树在一般决策树算法中，算是比较优的算法了，sklearn里面决策树算法也是使用的CART树的原理，我在研究中要使用这些基础算法的时候，一般都会使用sklearn里面的调用方法，直接调用。需要注意的就是ID3和C4.5可以是多叉树，但是CART树是一个二叉树。

对于问题1，CART树使用的是基尼系数，经济学指数也有个基尼系数，但是好像不一样。这里的基尼系数代表的是模型的不纯度，基尼系数越小，不纯度越低，特征越好，这个倒是和信息增益相反。公式如下

\[GiniIndex(D，A) = \sum\limits_{v = 1}^V\frac{|D^v|}{|D|}Gini(D^v) \]

假设数据有K类

\[Gini(D^v) = 1 - \sum\limits_{k=1}^{K}(\frac{|D^v_k|}{|D^v|})^2 \]

我们现在算一个特征的基尼系数看看，数据就用上面的

ID	年龄	有工作	信贷情况	类别
1	青年	否	一般	否
2	青年	否	好	否
3	青年	是	好	是
4	青年	否	一般	否
5	中年	否	一般	否
6	中年	否	好	否
7	老年	是	好	是
8	老年	是	非常好	是
9	老年	否	一般	否

计算特征年龄的基尼系数

\[GiniIndex(D，年龄) = \frac{4}{9}Gini(D，年龄 = 青年) + \frac{2}{9}Gini(D，年龄 = 中年) + \frac{3}{9}Gini(D，年龄 = 老年) \]

\[GiniIndex(D，年龄) = \frac{4}{9}(1 - (\frac{3}{4})^2 - (\frac{1}{4})^2)+ \frac{2}{9}(1 - (1)^2) + \frac{3}{9}(1 - (\frac{1}{3})^2 - (\frac{2}{3})^2) = 0.314 \]

对于问题2中的剪枝问题，一共有俩种常用的思想，一种是预剪枝，就是在决策树生成的时候，对每个节点在生成前先进行估计，如果当前节点的划分并不能给决策树带来泛化性能的提升，那么停止划分，并将当前节点标记为叶子节点，该叶子节点的类别就是训练数据最多的类别，第二种就是后剪枝，就是已经生成了一个完整的决策树，然后自底向上的对非叶节点进行考察，如果该节点对应的子树替换成叶子节点能够带来性能的提升，那么替换成叶子节点。先要考虑如何判断性能的提升，这里使用的就是留出法，将数据划分成训练集和验证集，验证集就是用来验证模型的泛化性能的。下面我们用一个例子来看看整个过程，

ID	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
4	青绿	稍蜷	浊响	清晰	稍凹	软粘	是
5	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	是
6	青绿	硬挺	清脆	清晰	平坦	软粘	否
7	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	否
8	乌黑	稍蜷	浊响	清晰	稍凹	软粘	否
9	浅白	蜷缩	浊响	模糊	平坦	硬滑	否
10	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	否

ID	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
1	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	是
2	浅白	蜷缩	浊响	清晰	凹陷	硬滑	是
3	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	是
4	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	否
5	浅白	硬挺	清脆	模糊	平坦	硬滑	否
6	浅白	蜷缩	浊响	模糊	平坦	软粘	否
7	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	否

上面10条数据就是测试集，下面7条数据就是验证集，我们先来看预剪枝。

预剪枝，计算每个特征的信息增益，这里我们就不计算了，第一个节点应该会选取脐部来进行划分，但是要先进行估计，如果不划分的话，所有的数据都在根节点中，那么选取数据最多的类别，是和否都是一样多，我们随便选择是，放入测试数据中，那么所有的测试数据都被分成是类别，最终的准确率就是\(\frac{3}{7} = 0.429\)，如果使用脐部进行划分的话，一共分为三个分支，如图

这里凹陷分支包含的数据是{1，2，3，7}，其中最多数据的类别就是类别是，那么类别就是好瓜，稍凹分支包含的数据是{4，5，8，10}，其中类别是和否都一样多，选择是，那么类别就是好瓜，平坦分支包含的数据是{6，9}，类别否最多，选择否，那么类别就是坏瓜，因而形成了三个分支。我们将验证集放进去，其中{1，2，3，5，6}分对了，准确率就是\(\frac{5}{7} = 0.714 > 0.429\)，那么可以进行分支。之后的结点都不会对准确率有提升，因此都会被剪枝掉。

从这个例子可以看出预剪枝使得很多分支都没有展开，确实降低了过拟合风险，减少了训练时间开销，但是这种贪心剪枝会给决策树带来欠拟合的风险，就像上图的决策树一样，只存在了一个特征，这就忽略了那些后续能够提升性能的划分，因而个人感觉后剪枝更好一点。

后剪枝，先从训练集中得到一颗完整的决策树，如下图所示

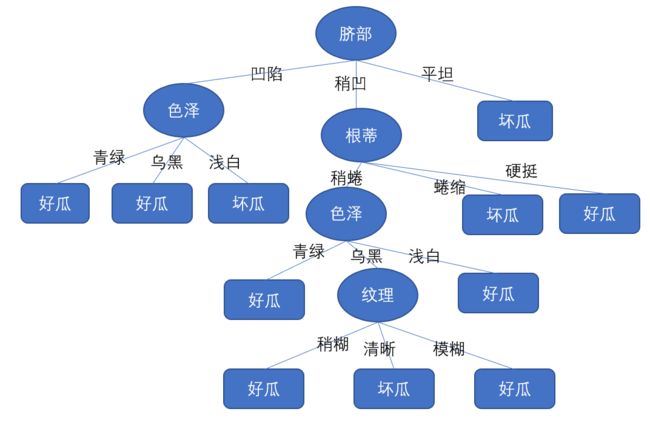
我们先从最下面的纹理特征开始，将之标记为叶子节点，节点中的数据是{5，8}，找出数据最多的类别，将这个叶子节点标记为好瓜，准确率得到了提升，成为了0.57，所以将之剪枝，之后看纹理上面的色泽，将之变成叶子节点，发现准确率并没有下降，因而可以不剪枝，之后再看上面的根蒂，发现也没有提升，之后再看根蒂左边的色泽，发现准确率提升了0.714，因此剪枝，因此最后的决策树应该如下图所示

可以看出后剪枝比预剪枝保留了更多的分支，后剪枝的欠拟合风险更小，泛化性能往往优于预剪枝，但是后剪枝是自底向上对每一个节点进行考察的，开销也更大。

决策树与条件概率分布

条件概率就是事件A在事件B已经发生条件下的发生概率，条件概率可以用决策树进行计算。决策树就是表示在给定特征条件下类发生的条件概率分布，决策树的一条路径就是特征空间中划分的一个单元，具体可以看下图

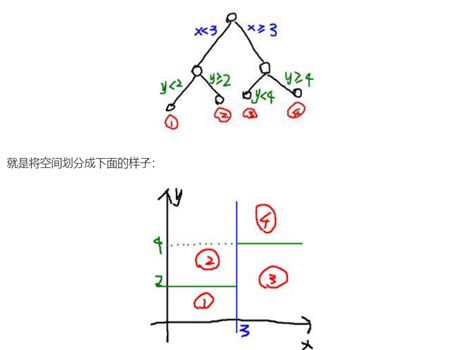
决策树的各个分支就是将特征空间划分成几个互不相交的单元或者区域，决策树的整个的条件概率分布就是各个单元给定条件下的类的条件概率分布组成的。

但是我们也可以从上图中可以看到它的划分都是与坐标轴平行的，这样虽然有可解释性，但是碰到复杂的分类边界的时候，必须要使用很多段划分才能得到近似结果，因此有了后来的多变量决策树，也称为斜决策树，就是可以实现更加复杂的划分边界，主要的算法就是OC1.

总结

决策树还是很好理解的，虽然如今，深度学习横行霸道，但是决策树依旧有着自己的优势，最重要的就是可解释性，这种优势让它可以用在根因分析中。并且它也不需要预处理，简单直观，更多的就是应用在小数据集中。决策树最重要的就是划分准则，上面的就是信息增益和基尼系数，虽然后来又有了很多划分准则，但是这些准则对性能影响较小，现在的很多决策树更多是CART树，比如sklearn中的决策树。决策树也与增量学习结合，就是接收到新的样本的时候，只需要对决策树进行调整即可，不需要重新学习，但是同时决策树对数据的波动很敏感，我觉得这主要还是决策树的拟合程度太高了。本文的代码都在我的github。