GNN Pooling(五):Self-Attention Graph Pooling,2019ICML
目录
- Graph Pooling
- Method
- Self-Attention Graph Pooling
- Model Architecture
- Experiments
- Datasets
- Setting
- Results
Graph Pooling
本文的作者来自Korea University, Seoul, Korea。话说在《请回答1988里》首尔大学可是很难考的,韩国的高考比我们的要更激烈乃至残酷得多。
本文提出了一种基于自注意的图池方法。使用图形卷积使我们的池化方法同时考虑节点特征和图形拓扑。为了确保公平的比较,对现有的池方法和我们的方法使用了相同的训练过程和模型架构。实验结果表明,该方法在参数合理的情况下,能够在基准数据集上取得良好的图分类性能。
池化层使CNN模型粗画图来减少参数的数量,从而避免过拟合。图池化方法可以分为以下三类:topology based, global, and hierarchical pooling。
- Topology based的使用的是图形粗化算法,而不是神经网络,这部分我也没看相关的论文就不做详细介绍了。
- Global pooling,代表作是Set2Set以及SortPool,这两篇都是之前博客读过的论文。
- Hierarchical pooling。代表是DiffPool以及gPool。
由于本文的方式是在U-Net所使用的gPool的基础上进行的改进,所以把gPool的公式列在下边:
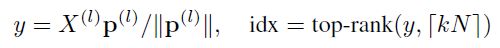

简单来说,gPool通过一个可学习向量p来计算不同特征投影分数,选择最高的k个特征进行保留,并且将保留之后的结点的拓扑结构A(l+1)从原来的结构A(l)中提取出来。但是图的拓扑结构并不影响投影得分,为了进一步改进图池,提出SAGPool,它可以使用特征和拓扑产生具有合理的时间和空间复杂度的层次表示。
Method
Self-Attention Graph Pooling
SAGPool的关键在于使用GNN进行self-attention的评分。假如使用Kipf的GCN作为卷积方式,那么self-attention score Z∈RN*1则可表示为:
![]()
这个与GCN传播的不同就在于θatt∈RN*1这个参数。A_hat = A + I,D_hat则表示degree matrix,X是特征。因为在上述的式子里既有结构A又有特征X,所以这个θatt这个参数是基于图的特征和拓扑结构的。如图1,首先卷积,然后top-K选择(也就是U-Net中对应的gPool池化)。这里有一个需要调节的超参数k∈(0,1],表示池化之后的结点的数量占原来的比例,池化之后的结果就为kN个了:
![]()
之后就需要根据idx对特征和结构进行选择了:
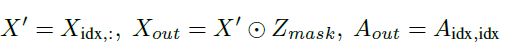
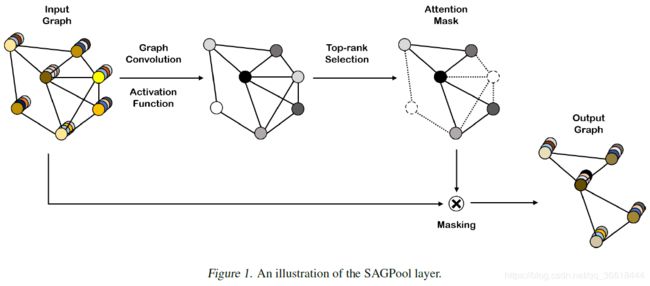
图中的Masking操作,也就是把根据top-K的id选出来的特征再乘一个Zmask,这个也比较好理解。可以使用不同的GNN代替GCN,所以计算Z的方法就可以泛化为:
![]()
除了使用邻居结点,使用多跳邻居或是任意的组合也都可以,为此,本文又提出了几种不同的改进策略:
![]()
A2表示two-hop的邻居,这个明显就是根据一-二阶邻居结点进行的计算。然后是两层GNN套娃:
![]()
然后是多重注意力得分平均,有点类似与Multi-head GAT:

以上三种不同的池化方式分别衍生出三个子方法: SAGPool_augmentation,SAGPool_serial , and SAGPoolparallel。这三位大兄弟将在后续的实验里进行对比,不过我们额外加点菜,看看SAGPool的源代码:
# torch_geometric据说是GNN的神器,这里面甚至封装了常用的GNN模型
from torch_geometric.nn import GCNConv
from torch_geometric.nn.pool.topk_pool import topk,filter_adj
from torch.nn import Parameter
import torch
class SAGPool(torch.nn.Module):
def __init__(self,in_channels,ratio=0.8,Conv=GCNConv,non_linearity=torch.tanh):
super(SAGPool,self).__init__()
self.in_channels = in_channels
self.ratio = ratio # 论文中的参数k
self.score_layer = Conv(in_channels,1) # 论文中的Z
self.non_linearity = non_linearity
def forward(self, x, edge_index, edge_attr=None, batch=None):
if batch is None:
batch = edge_index.new_zeros(x.size(0))
#x = x.unsqueeze(-1) if x.dim() == 1 else x
score = self.score_layer(x,edge_index).squeeze()
perm = topk(score, self.ratio, batch) # topk选择最大的几个
x = x[perm] * self.non_linearity(score[perm]).view(-1, 1) # mask
batch = batch[perm]
edge_index, edge_attr = filter_adj( # 选择子图结构特征
edge_index, edge_attr, perm, num_nodes=score.size(0))
return x, edge_index, edge_attr, batch, perm
Model Architecture
上文提到了GNN可以有很多种,本文还是用了Kipf的卷积(这不是废话吗):
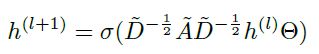
这个θ就是GCN中的参数,和θatt不是一个。
本文在输出之前添加了一个Readout layer把结点特征聚合成一个特定大小的表示。

xi一看就是特征,这个式子对x做了两种池化——平均池化和最大池化,然后拼接在一起。代码为:
from torch_geometric.nn import global_mean_pool as gap, global_max_pool as gmp
x1 = torch.cat([gmp(x, batch), gap(x, batch)], dim=1)
而对于具体的模型架构,本文使用了两种Global pooling architecture和Hierarchical pooling architecture,看图就知道了:

第一种和SortPool结构一样,三次卷积之后接一个池化;第二种是卷积一次池化一次,然后三次的输出拼接。
Experiments
Datasets
这次详细说一下数据集,之前都是跳过的。
- D&D。包含蛋白质结构的图表。节点表示氨基酸,如果氨基酸之间的距离小于6 °A(这个是专业术语?),则构造边,标签为蛋白质是酶还是非酶。
- PROTEINS。也是一组蛋白质。
- NCI。是一个用于抗癌活性分类的生物数据集。在数据集中,每个图表示一个化合物,节点和边分别表示原子和化学键。
- NCI1 and NCI109。用于图分类的基准数据集。
- FRANKENSTEIN。分子图包含连续值的节点特征。标签表示分子是诱变剂还是非诱变剂(凡是能引起生物体遗传物质发生突然或根本的改变,使其基因突变或染色体畸变达到自然水平以上的物质,统称为诱变剂)。
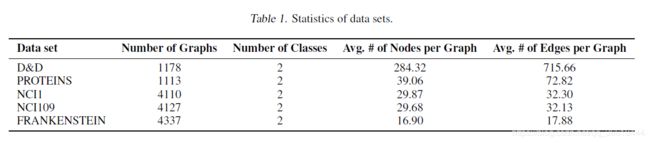
Setting
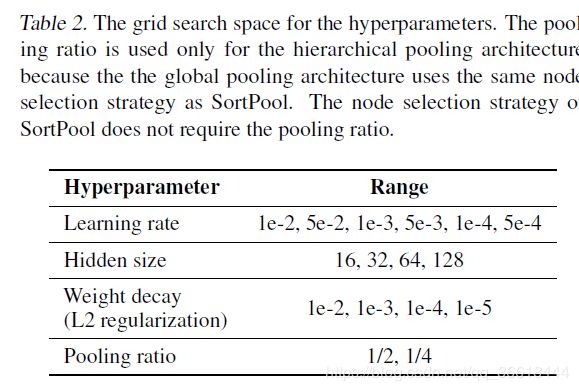
使用10倍交叉验证对20种随机种子的池化方法进行了评估。10%的训练数据用于在训练过程中进行验证。Adam优化,50 epoch early stop,100k epochs一共,grid search进行超参数选择,参数如table 2所示:
Results
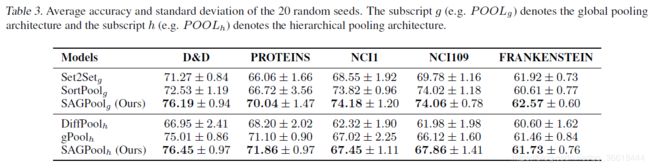
两种不同的架构分别和相似的模型进行比较,可以看到所有的数据集上准确率都更好。但是很难确定是全局池化架构还是分层池化架构完全有利于图的分类。由于全局池化架构(SAGPoolg, SortPoolg, Set2Setg)最小化了信息损失,它在节点较少的数据集(NCI1, NCI109, FRANKENSTEIN)上的性能优于分层池化架构POOLh (SAGPoolh, gPoolh, DiffPoolh)。然而,POOLh在具有大量节点(D&D,蛋白质)的数据集上更有效,因为它能有效地从大规模图中提取有用的信息。
参数数量讨论

对于基于gPool的方法来说,因为要学习的参数就只有一个θatt,这个取决于图的大小,因此SAGPool和gPool参数的量都是不变的。而DiffPool就不行了,参数蹭蹭上涨。
不同变体

讨论了SAGPoolh的情况下的变体,其中包括了不同的卷积方式,Cheb,SAGE,GAT,不同的注意力学习方式以及parallel的数量的影响。
Limitation
在SAGPool中,我们不能参数化池比率K来找到每个图的最优值,这个需要人工进行修改调参。