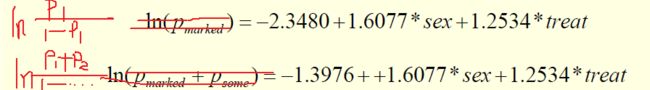数学建模之广义线性回归

EverydayOneCat

“ฅ”

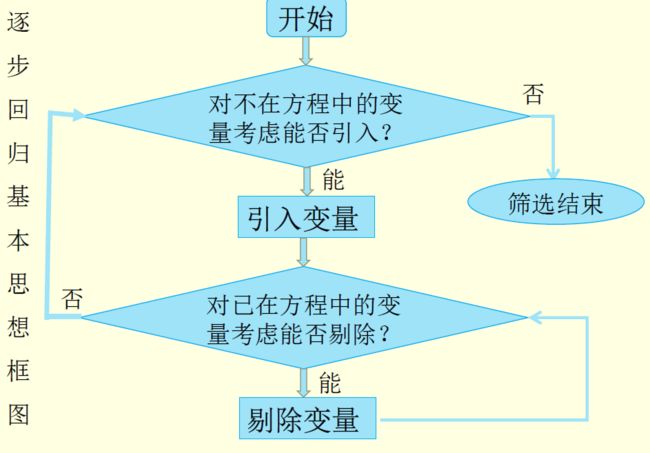
知识点

1.笔记

2.Logistic回归分析

2.1例一

例：研究不同治疗方法对某病疗效的影响

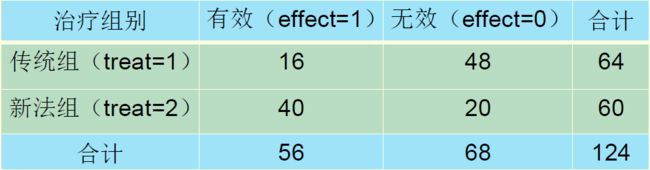
这种简单的数据可以直接通过计算得出

也可以编译SAS代码：

data a;
Input treat effect count@@;
cards;
1 1 16 1 0 48 2 1 40 2 0 20
;
proc logistic order =data;/*使用logistic回归*/
freq count;/*count为频数变量*/
model effect=treat;
run;

Logistic回归因变量信息表：

模型拟合检验表：

模型拟合检验表：

说明按照线性模型来做是没错的。

模型参数的最大似然估计表：

根据此可写出回归方程：
OR的点估计与区间估计表：

2.2例二

例2：研究性别及疾病严重程度对某病疗效的影响

这就涉及多个变量，编写SAS代码：

data a; Input sex degree effect count@@;
cards;
0 0 1 21 0 0 0 6 0 1 1 9 0 1 0 9 1 0 1 8
1 0 0 10 1 1 1 4 1 1 0 11
;
proc logistic descending;/*和order相反，这个是倒序*/
freq count;
model effect= sex degree/scale=none aggregate;/*scale=none aggregate是要求对模型进行拟合优度检验*/
run;

拟合优度检验表：

这里面的原假设H0：模型判断的结果和实际的结果没有差距。

说明：这两个统计量是用于刻画预测值与观测值之间的差异。当P值越接近于1，则其值越小，说明模型拟合的越好。

模型和模型参数检验：

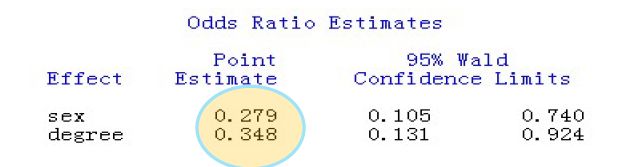
优势比的检验：（圈下来的就是优势比）

因为刚刚是desc降序，这时候看谁是1(分子)，优势比是1比0，也就是表示男性有效的治疗是女性的0.279倍，表示疾病严重有效的治疗是疾病不严重治疗的0.348倍。

说明男性的治疗效果比女性治疗效果差一些，严重的治疗效果比不严重的差一些。

2.3多分类自变量

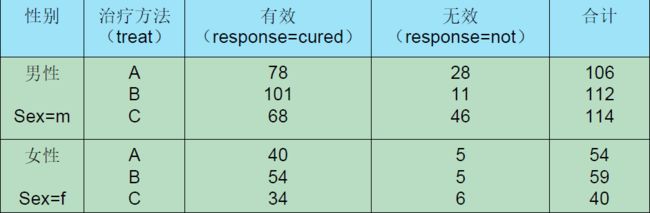
SAS代码：

data b; Input sex$ treat$ respone$ count@@;
dsex=(sex='m');/*规定sex=‘m’时，赋值为1*/
treata=(treat='A');/*规定treat=‘A’时，赋值为1*/
treatb=(treat='B');/*规定treat=‘B’时，赋值为1*/
cards;
m A cured 78 m A not 28 m B cured 101 m B not 11
m C cured 68 m C not 46 f A cured 40 f A not 5
f B cured 54 f B not 5 f C cured 34 f C not 6
;
proc logistic; freq count; 
model respone=dsex treata treatb/scale=none aggregate;
run;

这里面treata、treatb为哑变量，可以将多分类无序变量转化成水平数-1 的二分类变量。

由于没有规定顺序，先出来的就是分子。比方说dsex的m先出来，到了优势比就是m是分子；treata的A先出来，他的分子就是A；treatb同理。

这里拟合优度检验、模型和参数检验都和上面差不多，就不着重分析了，我们主要来看优势比检验。

m/f=0.382，男性优势不如女性优势。
A/C=1.795，B/C=4.762，说明ABC三种药物B药效最好，A其次，C最差。

2.4连续型变量

研究学生的成绩对考研成功与否的影响。

SAS代码：

data study; Input ky shu1 shu2 shu3@@;
cards;
0 84 63 74
0 89 71 88
1 98 92 98
0 83 63 60
0 93 78 72
;
proc logistic des;
model ky=shu1 shu2 shu3 /selection=stepwise;/*采用逐步回归法*/
run;

入选模型的剔除检验表：

高等代数1，高等代数2，线性系统理论等对于考研的影响很显著。

入选模型的参数估计：

依据此写出回归方程：

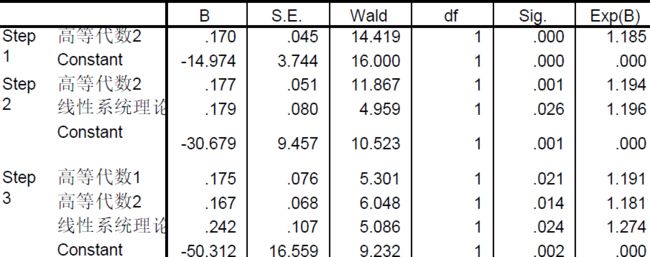
做一个预测表：

由上表知：预测准确率达24/26=92.3%。

2.5多分类因变量

研究性别及疾病严重程度对某病疗效的影响

对于这种多分类因变量，我们通常把部分看成整体来求

SAS代码：

data ex;input sex treat effect$ count@@;
cards;
1 1 marked 16 1 1 some 5 1 1 none 6
1 0 marked 6 1 0 some 7 1 0 none 7
0 1 marked 5 0 1 some 2 0 1 none 7
0 0 marked 1 0 0 some 0 0 0 none 10
;
proc logistic order=data;
freq count;
Model effect=sex treat/scale=none aggregate;
run;

3.Probit回归

标准正态分布的密度和累积正态分布函数图:

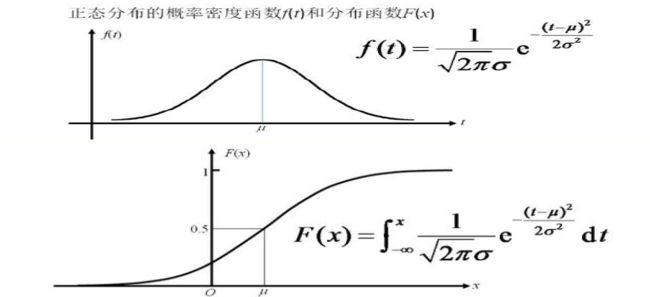
SAS实现：

data a;
Input @@;
cards;
;
proc logistic des;
model /link=probit;/*实现Probit回归法*/
run;

Logit转换与Probit转换的对比图：

1）当自变量中分类变量较多时，用Logistic回归；当自变量中连续性变量较多且服从正态分布时，用Probit回归；
2）Logistic回归的系数可以得到很好的解释，而Probit回归的系数解释起来较麻烦。
4）实际中Logistic回归与Probit回归分析的结果非常接近。

作业

上班方式的影响因素分析及预测
Y表示骑车上班(Y=1bike,Y=0,BUS),X1年龄,X2月收入,X3性别(1男,0女)。数据见下表。请回答下列问题。

1. 建立上班出行方式的logit回归模型，并作相应的统计检验。
2. 结合模型，分析上班方式的影响因素？影响大小顺序是怎样的？
3. 检验模型的预测功能，并预测第29-32个人的出行方式会是怎样的？

人员序号	X1	X2	X3	y
1	18	850	0	0
2	21	1200	0	0
3	23	850	0	1
4	23	950	0	1
5	28	1200	0	1
6	31	850	0	0
7	36	1500	0	1
8	42	1000	0	1
9	46	950	0	1
10	48	1200	0	0
11	55	1800	0	1
12	56	2100	0	1
13	58	1800	0	1
14	18	850	1	0
15	20	1000	1	0
16	25	1200	1	0
17	27	1300	1	0
18	28	1500	1	0
19	30	950	1	1
20	32	1000	1	0
21	33	1800	1	0
22	33	1000	1	0
23	38	1200	1	0
24	41	1500	1	0
25	45	1800	1	1
26	48	1000	1	0
27	52	1500	1	1
28	56	1800	1	1
29	49	1200	1
30	36	900	1
31	28	1200	0
32	55	1150	0

1.第一问

由于自变量x1,x2不是分类变量而是连续型的变量，所以在建立回归模型时使用逐步回归法，找出对上班方式影响显著的因素。

编写SAS代码：

data a;
input x1-x3 y@@;
cards;
18	850	0	0
21	1200	0	0
23	850	0	1
23	950	0	1
28	1200	0	1
31	850	0	0
36	1500	0	1
42	1000	0	1
46	950	0	1
48	1200	0	0
55	1800	0	1
56	2100	0	1
58	1800	0	1
18	850	1	0
20	1000	1	0
25	1200	1	0
27	1300	1	0
28	1500	1	0
30	950	1	1
32	1000	1	0
33	1800	1	0
33	1000	1	0
38	1200	1	0
41	1500	1	0
45	1800	1	1
48	1000	1	0
52	1500	1	1
56	1800	1	1
;
proc logistic descending;
model y=x1-x3/scale=none aggregate selection=stepwise;
run;

可以看出，最后进入模型的是 x1年龄因素和 x3性别因素，因此认为年龄因素和性别因素对于上班方式的影响显著，而根据数据没有证据说明月收入因素对于上班方式的影响显著。

接着我们看模型显著性检验：

原假设为Logistic 回归方程的所有系数全为零，即因变量Y 与自变量线性无关. 通过检验，结果如上表所示. 每种检验的P 值均小于0.05，接受备择假设，拒绝原假设，所以因变量Y 与自变量线性相关. 说明可以选择Logistic 回归模型.

拟合优度检验表：

都大于0.05，接受原假设：模型判断的结果和实际结果没有差距，说明模型拟合的很好。

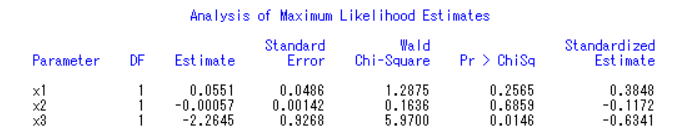
参数估计：我们使用最大似然法来估计回归方程中的B，并用Newton-Raphson 迭代算法，求出参数的最大似然估计.

可以看出x1,x3 两个因素是上班方式的影响因素。常数项的卡方检验值为2.8620，P 值为0.0907 大于0.05 所以接受原假设认为等于0，而x1,x3 的卡方检验值分别为4.9856 和4.5059，P 值分别为0.0256 和0.0338 均小于0.05 所以拒绝原假设，认为B1和B3 不等于0，所以回归方程为：即

优势比估计OR 的点估计与区间估计：

可以看出x1 年龄因素中年龄大的骑自行车概率是年龄小的1.108 倍，x3 性别因素中男性骑自行车的概率是女性的0.108 倍，所以认为年龄较大的女性骑自行车的概率更大。

2.第二问

SAS代码：

data a;
input x1-x3 y@@;
cards;
数据区
;
proc logistic descending;
model y=x1-x3/noint stb;
run;

可以看出，经过标准化之后的变量系数的大小分别为 x3,x1,x2，所以得出结论性别因素是三个影响因素中最能够影响上班方式的因素，其次是年龄因素，影响最小的是月收入因素。

综合以上分析，得出结论影响上班方式的因素的影响大小顺序为：性别 >年龄 >月收入

3.第三问

由问题一中的拟合优度检验可以知道，用Logistic 回归模型判断出的结果和原始的结果数据没有差距，说明模型的预测能力很好。

SAS代码：

data a;
input x1-x3 y@@;
cards;
数据区
49	1200	1 .
36	900	1 .
28	1200	0 .
55	1150	0 .
;
proc logistic descending;
model y=x1-x3/scale=none aggregate selection=stepwise;
proc reg;model y=x1 x3/noint cli;
run;

预测出第29-32个人的出行方式分别为骑自行车、乘公交、骑自行车、骑自行车。

结语

包弟，我能去你家过年吗

乐言？批言！