数据结构错题集整理
第二章:线性表
第三章:栈与队列
只要队列不满就可以进行进队列操作,只要队列不空就可以进行出队列操作,并不规定进队列、出队列操作的次序。
因为无论出队和入队,都要进行求余运算,将队首指针和队尾指针转化为有效的顺序队下标值,另外,循环顺序队中的元素可以平行移动,所以本叙述是正确的。
第五章:数组和广义表
按下三角保存,而不是保存三对角矩阵。
数组的基本操作有存取、修改、检索和排序等,没有插入与删除操作。
tail取出的结果要用()存放,head取出来的不用。
应该不用考虑对角矩阵,但是考虑的话有可能小于50%,如:三对角矩阵压缩率为(3*n-2)/(n*n),当n=10,压缩率为28/100。
第六章:树
不是字母顺序不同,而是形状不同。
叶子节点个数等于度为2的节点个数+1
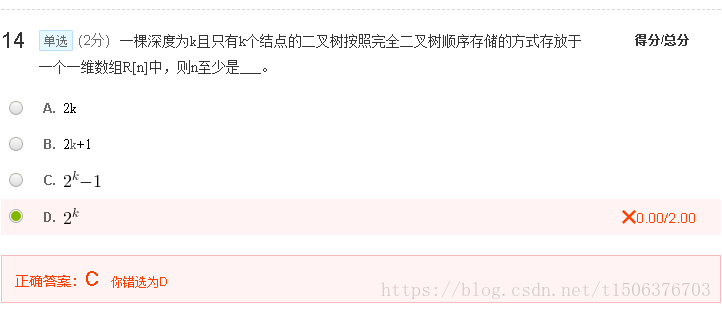
注意:至少
后序遍历比较合理。正常的逻辑应该就是:做好当前结点子树内部的交换,然后交换当前结点的左右子树。刚好符合后序遍历的算法逻辑。
1. 交换好左子树
2. 交换好右子树
3. 交换左子树与右子树
前序遍历(中左右)、中序遍历(左中右)的最后访问的节点都是左或右叶节点,叶节点是没有子树的,所以两个指针域空出来了,可以存放线索指针。但是后续遍历(左右中),最后访问的子树的根节点,子树根节点的两个指针域都指向子树了,所以不能空出来存放线索信息。
第七章:图
注意确保2字,如果只是成为连通图,5条也可以。加上确保后,前4个定点两两相连,(4*(4-1))/ 2,再加上1条,答案为7
注意至少,我们假设n个定点的完全图有10条边,n等于5,为了使其成为非连通图,再增加一个点。
要注意,本题问的是有向图。要使具有n个结点的有向图是连通图,则至少要n个结点,也就是让这n个结点组成一个环。
最小生成树是指连通网的所有生成树中权值之和最小的生成树。
易混淆概念:
连通图的极小连通子图成为生成树。
从反面理解,如果n个顶点的有向连通图构成强连通图,至少有n条边。
连通分量是极大连通子图。
最多为n*(n-1),已经超过了。
无向图的邻接多重表,每个顶点、边都只有一个节点。
不太懂,应该是e个顶点吧。
有向图邻接表的空间复杂度为O(n+e),有向图邻接表的空间复杂度为O(n+2*e)
注意,是连通图。
普里姆(Prim)算法 ,时间复杂度为O(n2),适合于求边稠密的最小生成树;kruskal算法时间复杂度e*log2e,适合稀疏图。
也有可能本生就是最小生成树,但是有相同的权值。
从源点到汇点的最长路径为关键路径,深度优先不能保证是最长的,答案应该是拓扑排序。
第九章:查找
这类型题的关键是画出判定树,算出结果为小数时,两个整数都可能。。
关键问题是创建平衡二叉树。
假设为满二叉树,即长度为63,此时至少比较6次,而题中,至少只需要5次。
可以理解为在查找的过程中建立起哈希表。
注意:没有涉及到提高存储效率的内容。
最少4个点,最多7个点,依次画出来。
对于分块查找,如过采用顺序查找确定待查值可能所在的块,asl=(n/s+s)/2+1
直接定位法就可以实现。
这个不一定,要看查找的内容。
单链表不适合。
仔细想一下,确实不对,有可能相同。
对于相同的关键字集,如果不同的初始序列,那么创建的平衡二叉排序树不一定相同。
对的,不存在旋转,如果是平衡二叉排序树就不对了。
没有要求每块的数据一定相同。
二叉排序树查找法能适应查找表中数据的动态变化的要求。
高为5的平衡二叉树至少有12个节点,反过来,12个节点,最多有5层高。
第10章:排序
![]()
堆分为大堆和小堆,要么全大于,要么全小于。
这个答案好像有问题,个人觉得两遍后不是那个结果。
最后一个元素的时候,有n+m-1个已经排好序。
归并算法在合并的时候,需要开辟一个与原数组相等的空间。
不太懂。
快速排序空间复杂度为O(log n),其他为O(1)
简单插入排序是稳定的,找到比自己大的才停止,所以后面的元素相对位置还是在后面。
在以下两种情况时,快排性能最差:(1)在分解时每次选取的主元素为最小元素,(2)在分解时每次选取的主元素为最大元素,而在初始有序的条件下就满足上面的情况。
选择排序包括:(1)堆排序(2)简单选择排序
就是时间复杂度计算吧,n*lon2n,结果为24
初始有序,快排效率最低,时间复杂度O(n2)
选择排序一定是n-1趟排序,比较的次数永远是n(n-1)/2