openssl源代码方式安装以及简单的实验

一、引言

这仍然是信息安全课程的一次作业，老师的要求包括以源代码方式来安装openssl，了解AES和RSA加密算法并去尝试调用openssl库中AES和RSA算法的API，其实总体上安装以及实验还是比较容易的，不过还是踩了一些坑，这里还是记录一下，顺便试试CSDN的Markdown编辑器。

本文演示使用的操作系统为Ubuntu 16.04

二、安装

1.下载源码包

从官网上可以找到源码包的下载，这里我直接给出下载链接：
openssl源码包下载
根据官网的描述，1.1.1版本将是目前他们长期支持的版本，一直到2023年，建议使用1.0.x版本的用户也去安装这个最新版本。

2.编译安装

解压下载的源码包，可以看到如下的目录结构

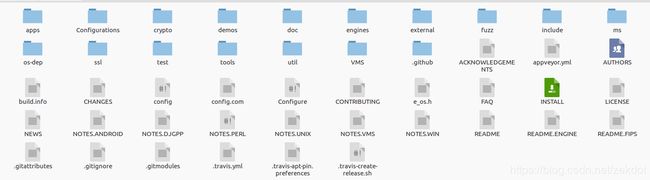可以点开INSTALL文件来查看安装说明，这里我们按照它说的最简说明方式来进行安装：

on Unix (again, this includes Mac OS/X):

$ ./config
$ make
$ make test
$ sudo make install

其中最后一条命令如果不是root用户执行，需要加上sudo，否则无法访问系统根目录的一些文件夹，至少我第一次没加sudo运行时报了错。

这四条命令运行完之后都没有报错的话，说明它的安装脚本中的所有任务都完成了，这时可以使用

openssl version

命令来查看当前openssl的版本，不过我在这时遇到了问题，报错是这样的：

openssl: error while loading shared libraries: libssl.so.1.1: cannot open shared object file: No such file or directory

通过查找资料，这个问题也很容易就解决了，原因大概是因为libssl.so.1.1被安装脚本放置到了/usr/local/的lib下，而命令行调用的时候找的是/usr/的lib下的libssl.so.1.1，所以我们只需要用如下两条命令在/usr/的lib下创建链接文件即可：

ln -s /usr/local/lib/libssl.so.1.1 /usr/lib/libssl.so.1.1
ln -s /usr/local/lib/libcrypto.so.1.1 /usr/lib/libcrypto.so.1.1

值得一提的是，我百度到的命令的lib文件夹命名为lib64，这里一定要结合自己的情况去查看，不要直接复制命令去运行。

在解决这个问题之后，再运行之前的openssl version命令就会出现如下的显示，也说明安装成功了：

OpenSSL 1.1.1  11 Sep 2018

三、运行

1.MD5算法的实验

首先来实验一下最简单，也是最常用的MD5摘要算法，说它简单是因为它的API只有三个，用来试运行再好不过了，这里我也是参照了一位博主的一个例子来实验的，更详细的讲解可以看这篇博客：

Linux下C语言使用openssl库进行加密
用到的代码也是直接搬过来使用的，这里贴一下吧：

#include 
#include 
#include 
int main()
{
	MD5_CTX ctx;
	unsigned char outmd[16];
	int i=0;

	memset(outmd,0,sizeof(outmd));
	MD5_Init(&ctx);
	MD5_Update(&ctx,"hel",3);
	MD5_Update(&ctx,"lo\n",3);
	MD5_Final(outmd,&ctx);
	for(int i=0;i<16;i++)
	{
		printf("%02X",outmd[i]);
	}
	printf("\n");
	return 0;
}

这里是我遇到的另外一个坑，如果用gcc编译的话，会出现如下的情况：

$ gcc md5test.c 
/tmp/ccP3aNqM.o：在函数‘main’中：
md5test.c:(.text+0x42)：对‘MD5_Init’未定义的引用
md5test.c:(.text+0x58)：对‘MD5_Update’未定义的引用
md5test.c:(.text+0x6e)：对‘MD5_Update’未定义的引用
md5test.c:(.text+0x81)：对‘MD5_Final’未定义的引用
collect2: error: ld returned 1 exit status

通过百度，这个问题也很好解决，只需要引用链接库crypto即可，如下所示：

$ gcc md5test.c -lcrypto && ./a.out
B1946AC92492D2347C6235B4D2611184

2. AES对称加密算法API调用实验

使用API之前，最好先简单了解一下AES算法的原理（虽然调用API的话并不需要搞清楚算法实现），这里我贴出一个博主的博客，感觉讲的还是挺好的
AES加密算法的详细介绍与实现
而实验部分的API我也参考了另一位博主的博客：
OPENSSL库的使用-AES篇

#include 
#include 
int main()
{
	AES_KEY key;	//新建一个AES_KEY
	unsigned char userkey[]="test";	//密钥字串
	unsigned char in[]="this is data";	//要加密的信息
	unsigned char out[13];	//密文
	int res=AES_set_encrypt_key(userkey,128,&key);	//设置加密秘钥

	AES_ecb_encrypt(in,out,&key,AES_ENCRYPT);	//设置解密秘钥
	puts(out);			//打印密文
	res=AES_set_decrypt_key(userkey,128,&key);	//设置解密秘钥
	
	unsigned char out2[13];	//保存解密后的字串
	AES_ecb_encrypt(out,out2,&key,AES_DECRYPT);	//解密
	puts(out2);	//打印解密后的信息
	return 0;
}

这里的运行结果太鬼畜了，我贴一下图吧：

3.RSA算法API调用实验

RSA算法还是感觉挺神奇的，这里也是贴出一篇学习的时候参考的博客：
对称加密与非对称加密，以及RSA的原理
博主文尾举的例子好像有错误，我也在评论中写出来了，不过这篇文章依然极具参考价值。
实现部分，我参考了两位博主的代码：
OPENSSL库的使用-RSA篇
如何利用OpenSSL库进行RSA加密和解密

代码如下：

#include 
#include 
#include 
RSA * get_rsa(long e,int bit)
{
	RSA * rsa=RSA_new();	//新建RSA结构体指针
	if(rsa==NULL)
		return NULL;
	BIGNUM *eNum=BN_new();	//新建一个大数结构体对象
	if(!BN_set_word(eNum,e))	//设置算法中的e
		return NULL;
	if(!RSA_generate_key_ex(rsa,bit,eNum,NULL))	//调用API生成RSA结构体
		return NULL;
	return rsa;
}
int main()
{
	RSA *rsa=get_rsa(0x10001,1024);	//利用e为0x10001(65537)生成一个模数n为1024的rsa指针
	//RSA_print_fp(stdout,rsa,0);		//执行这句话可以打印出生成的十六进制格式的模数n、两个质数p、q等
	unsigned char in[]="Hello World";	//要加密的明文
	unsigned char out[2048];	//保存加密后的信息
	unsigned char res[120];	//保存解密后的信息，长度要小于RSA_size(rsa)

	//用于加解密传输：
	puts(in);	//打印明文
	printf("%d\n",RSA_public_encrypt(strlen(in)+1,in,out,rsa,RSA_PKCS1_PADDING));	//公钥加密明文生成密文
	puts(out);	//打印密文
	printf("%d\n",RSA_private_decrypt(128,out,res,rsa,RSA_PKCS1_PADDING));	//私钥解密密文
	puts(res);	//打印解密后的密文

	//用于签名和验签：
	printf("%d\n",RSA_private_encrypt(strlen(in)+1,in,out,rsa,RSA_PKCS1_PADDING));	//私钥加密明文生成密文
	puts(out);//打印密文
	printf("%d\n",RSA_public_decrypt(128,out,res,rsa,RSA_PKCS1_PADDING));	//公钥解密
	puts(res);	//打印解密后的密文

	RSA_free(rsa);	//释放rsa结构体内存
	return 0;
}

这里我封装了生成RSA结构体指针的过程，RSA指针中保存着之前原理中提过的n、p、q、e等BIGNUM类型的数据，似乎在1.1.1版本之前还可以查看值，但是我尝试去获取这些数据时会报错：

rsatest.c:20:32: error: dereferencing pointer to incomplete type ‘RSA {aka struct rsa_st}’
printf("%d\n",BN_num_bytes(rsa->n));

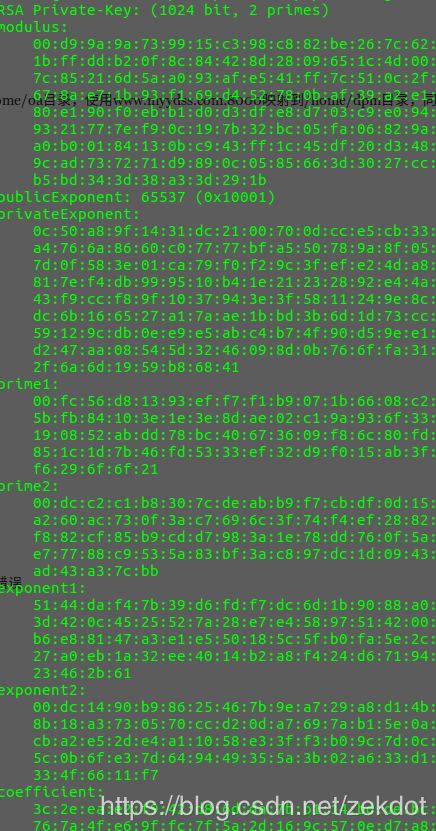
所以如果想查看rsa生成的东西的话，可以使用RSA_print_fp(stdout,rsa,0)函数，效果如下：

这里调用RSA_generate_key_ex(rsa,bit,eNum,NULL)传入的bit参数即为生成的rsa指针中的模数的位数，小于512的话会报段错误，其实我本来还想试试能不能生成原理中举的那个n为143的例子来着，看来也是根本不可能。

此外注意，保存解密后的信息的数组，长度要小于RSA_size(rsa)函数的返回值（违反这个规则的话是无法完成解密的，解密结果是乱码）我这里由于modulus(之前提到的bit参数)是1024,1024/8=128，所以长度设为了120，如果改变了modulus的大小，这里也要对应的改变。

最后来测试效果，也是比较鬼畜，所以直接截图了：

可见算法运行正确。

最后通过查阅相关资料得知，RSA加密算法有两种用途：

第一种用法：公钥加密，私钥解密。---用于加解密
第二种用法：私钥签名，公钥验签。---用于签名