频繁项集与关联规则(英文版)
Introduction
The study of Finding frequent item-sets and association rules is an important part of Data Mining , which has been widely applied to optimize marketing strategies, enhance the performance of recommendation as well as outlier detection.This report introduces some related concepts and A-priori algorithm ,which effectively discovers frequent item-sets by scanning data set twice for each iteration. Sequentially, experiments are conducted and analyzed. Finally, a short conclusion is made for further understanding of finding frequent item-sets and association rules.
Related concepts
Let U = {u1,u2,…,um} and I = {i1,i2,…,in} be the set of baskets and items, respectively. Here , m and n are the number of baskets and items respectively. More notations related to the concept of frequent item-sets and association rules are listed in Table 1:

Given the item-set i and item-set j, sij denotes the number of those baskets where item-set i and item-set j are both contented. Smin is the threshold , also call as critical value, to segregate the frequent item-sets and non-frequent item-sets.cij represents the probability of occurrence of item-set j assuming item-set i already exists. insij represents a difference value between cij and the frequency of item-set j, which is beneficial when the support of item-set i is much larger than that of item-set j. The formula of cij and insij are defined as follows:

A-priori
In practice, to find frequent item-sets is most essential and challenging especially when the data set is too huge and overwhelming for main memory. Therefore, a-priori algorithm was proposed in early year to improve the utilization of main memory and reduce the space for scanning data set. The monotonic characteristic of frequent item-sets is emphasized , stating if item-set i is a frequent item-set, then all of its subset are also frequent item-sets. On the contrary, if one of the subset is not a frequent item-set, item set i is definitely not a frequent item-set.
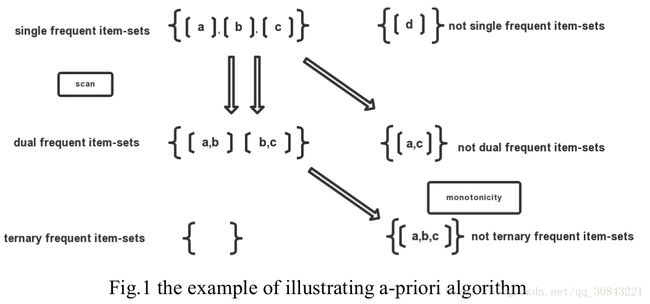
Firstly, a-priori algorithm scans the data set once to find single frequent item-sets. Owing to monotonicity, dual frequent item-sets only derives from those in single frequent item-sets. Consequently, on the second scan, we only focus on the the dual item-sets combined by any two single frequent item-sets and check its support with a given support threshold smin to decide whether it belongs to dual frequent item-sets, similar to the way of finding ternary frequent item-sets and higher frequent item-sets. Figure 1 clarifies the process of how a-priori works:
Experiment and analysis
To demonstrate the performance of a-priori algorithm, we implement it by python and put it on Github (https://www.github.com/Quincy1994/Apriori), where we can find the code and some related data.A visual tool called igraph is employed for describing the distribution of frequent item-sets.
In this report, the data set from the 2017 SMP CUP is used to test a-priori algorithm, providing the 1043 users in CSDN platform and their related blogs.We collect the titles from each user’s related blogs to establish different documents, and each document contains all the titles of related blogs for each user.An example of these documents is presented in Table 2.
We tokenize these titles and remove some stop words and single words as well as punctuation marks, remaining the main terms.We treat users’ documents as baskets while terms in document are seen as items.

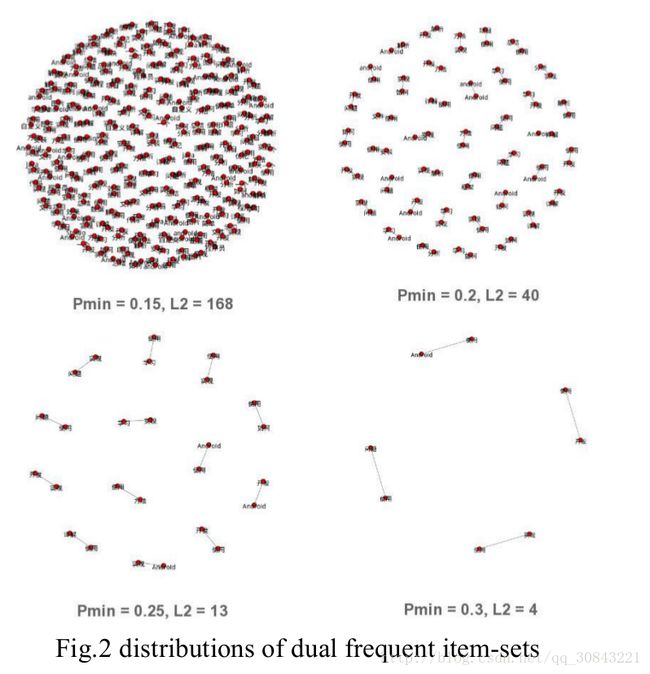
Considering that a relative support threshold is more adaptive to different data set than the absolute support threshold, we use pmin (smin = pmin* m) to reshape the value of smin . L1, L2,L3 represent the number of single frequent item-sets, dual frequent item-sets and ternary frequent item-sets, respectively. Table 3 shows the results on a-priori algorithm with different values of pmin , and the distributions of dual frequent item-sets and ternary frequent item-sets are presented on Figure 2 and Figure 3:
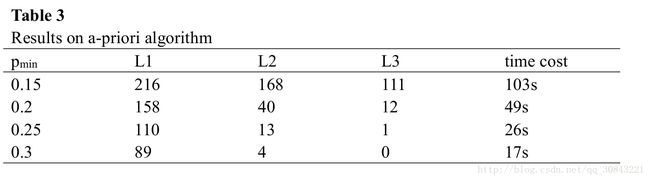
The experimental results on Table 3 reveal that, L2, L3 and cost of time shrink sharply with the increase of Pmin, which demonstrates that the advantage of a-prior algorithm by the virtue of monotonicity of frequent item-sets to decrease the cost of counting numbers of item-sets.

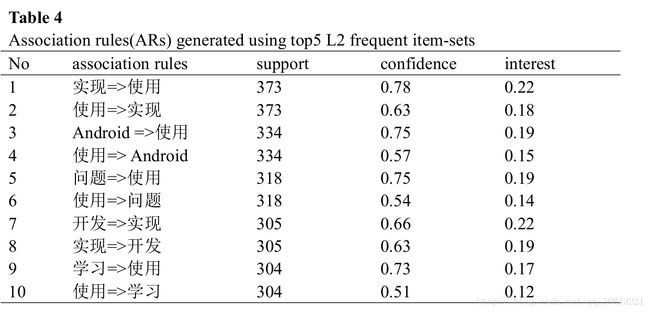
The association rules are identified using confidence and interest from top-5 L2 frequent item-sets generated by the a-priori algorithm.Table 4 shows that the two confidences generated from the same frequent item-sets are not symmetric.In addition, though confidence and interest can be used to discover the frequent item-sets, there are no linear relation between them.
Conclusion
Because of their simplicity and practicality, frequent item-sets and association rules have been used in various applications and data sets. This report introduces some related concepts and an efficient method, a-priori algorithm, for discovering frequent item-sets.Experimental results from the survey data reveal that the a-prior algorithm is enable to improve the efficiency significantly.
However, several issues remain to be addressed.First, the documents regarded as “basket” are contented with at least 50 items, some of which are rare among all the documents and uselessness.Second, the a-prior algorithm treats each item as the same weight while in practical, items are often weighted with different values to represent their different importance. Finally, the question of which variable is better, confidence or interest, to measure the probability of an association rule in different situations is still not answered clearly.