SVM学习总结（三）SMO算法流程图及注释源码

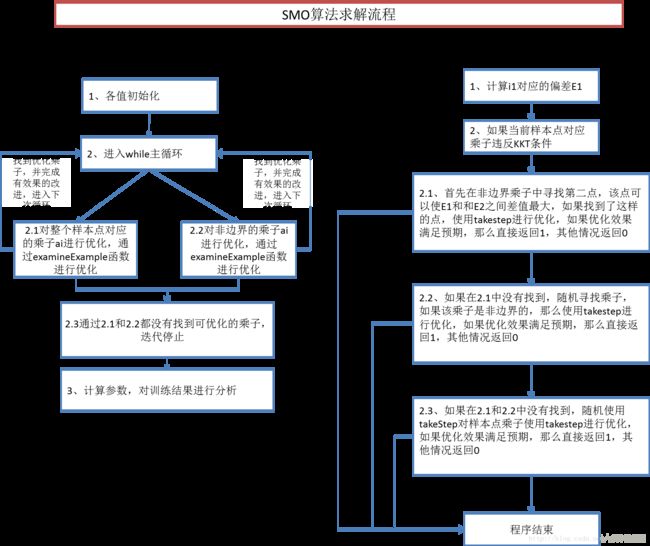
一、SMO算法流程图

算法中的流程图绘制是根据第二节中的源码绘制的。

二、SMO算法C++源码

下面的源码是在csdn上下的，非常适合初学者的，而且smo算法实现的主体架构和实现都与SMO算法原论文基本一致，源码应该是一个老外写的，英文注释较多，csdn上下的适合有些中文注释，我在看的过程中又加入了一些注释，注释中提到的书指的主要是李航的《统计学习方法》。

1、smo.h文件

//#include "iostream.h"
//#include "fstream.h"
#include
#include
#include "ctype.h"
#include "math.h"
#include "stdlib.h"
#include "time.h"
using namespace std;
#define N 27//样本数总数
#define end_support_i 27
#define first_test_i 27
#define d 13//维数
//////////global variables
//int N=     //样本数
//int d=     //维数
int C=100;//惩罚参数
double tolerance=0.001;//ui与边界0,C之间的公差范围
double eps=1e-3;//一个近似0的小数
int two_sigma_squared=100;//RBF(Radial-Basis Function)核函数中的参数。sigma==(10/2)^1/2。
double alph[end_support_i];//Lagrange multipiers
double b;//threshold
double error_cache[end_support_i];//存放non-bound样本误差
int target[N];//训练与测试样本的目标值
//double precomputed_self_dot_product[N];//预存dot_product_func(i,i)的值，以减少计算量
double dense_points[N][d];//存放训练与测试样本，0-end_support_i-1训练;first_test_i-N测试

//函数的申明
int takeStep(int,int);
int examineNonBound(int);
int examineBound(int);
int examineFirstChoice(int,double);
int examineExample(int);
double kernel_func(int,int);
double learned_func(int);
double dot_product_func(int,int);
double error_rate();
void setX();//设置样本值矩阵
void setT();//设置目标值向量
void initialize();
///////////////////////////////////////////////////////

2、smo.cpp文件

//C-Support Vector Classification(Binary Case)
//The advantage of SMO(Sequential Minimal Optimization) Algorithm lies in the fact that solving for
//two Lagrange multipliers can be done analytically.

/*
There are three components to SMO:
(1)an analytic method to solve for the two Lagrange multipliers.
(2)a heuristic(启发式的)for choosing which multipliers to optimize:
    SMO will always optimize two Lagrange multipliers at every step, with one of the Lagrange multipliers 
having previously violated the KKT conditions before the step. That is, SMO will always alter two Lagrange
multipliers to move uphill in the objective function projected into the one-dimentional feasible subspace.
    There are tow separate choice heuristics: one for the first Lagrange multiplier and one for the second.
The choice of the first heuristic provides the outer loop of the SMO algorithm. The outer loop first iterates
over the entire training set, determing whether each example violates the KKT conditions. If an example violates
the KKT conditions, it is then eligible for immediate optimzation. Once a violated example is found, a second
multiplier is chosen using the second choice heuristic, and the two multiplers are jointly optimized.
    Once a first Lagrange multipler is chosen, SMO chooses the second Lagrange multiplier to maximize the 
size of the step taken during joint optimization.
(3)a method for computing b:
    After each step, b is re-computed.
*/
//The kernel function is RBF(Radial-Basis Function).

#include "smo.h"

void main()
{
    ofstream outClientFile("data_result.txt", ios::out);//如果指定的文件data_result.txt不存在，ofstream就用该文件名建立它。
    int numChanged=0;
    int examineAll=1;
    //srand((unsigned int)time(NULL));
    initialize();//样本值开始赋值
    //以下两层循环，开始时检查所有样本，选择不符合KKT条件的两个乘子进行优化，选择成功，返回1，否则，返回0
    //所以成功了，numChanged必然>0，从第二遍循环时，不从整个样本中去寻找不符合KKT条件的两个乘子进行优化，
    //而是从非边界乘子中去寻找，因为非边界样本需要调整的可能性更大，边界样本往往不被调整而始终停留在边界上。
    //如果没找到，再从整个样本中去找，直到整个样本中再也找不到需要改变的乘子为止，此时算法结束。
    while(numChanged>0||examineAll)
    {
        numChanged=0;
        if(examineAll)
        {
            for(int k=0;k//examine all examples
            }
        }
        else
        {
            for(int k=0;kif(alph[k]!=0&&alph[k]!=C)
                    numChanged+=examineExample(k);//loop k over all non-bound Lagrange multipliers
            }
        }
        if(examineAll==1)
        {
            examineAll=0;
        }
        else if(numChanged==0)
        {
            examineAll=1;
        }
        /*
        The examples in the non-bound subset are most likely to violate the KKT conditions.
        */
    }
    //存放训练后的参数
    {
        outClientFile<<"d="<//维数
        outClientFile<<"b="<//threshold
        outClientFile<<"two_sigma_squared="<int n_support_vectors=0;
        for(int i=0;iif(alph[i]>0)//此地方是否可以改为alph[i]>tolerance?????????????????
            {
                n_support_vectors++;
            }
        }
        outClientFile<<"n_support_vectors="<//输出支持向量个数
        outClientFile<<"rate="<<(double)n_support_vectors/first_test_i<//支持向量在样本数量中的占比
        for(int i=0;iif(alph[i]>0)
            {
                outClientFile<<"alph["<"]="<//输出alph值
            }
        }
        outClientFile<//输出，以及测试
    //cout<
    system("pause");
}

/////////examineExample程序
//假定第一个乘子ai(位置为i1)，examineExample(i1)首先检查，如果它超出tolerance而违背KKT条件，那么它就成为第一个乘子；
//然后，寻找第二个乘子(位置为i2),通过调用takeStep(i1,i2)来优化这两个乘子。
int examineExample(int i1)
{
    int y1;
    double alph1,E1,r1;
    y1=target[i1];//当前样本的类别
    alph1=alph[i1];//当前样本对于的alph值，alphi在initialize();中的初始化为0.0。
    if(alph1>0&&alph1//支持向量
        E1=error_cache[i1];
        /*
        A cached error value E is kept for every non-bound training example from 
        which example can be chosed for maximizing the step size.
        */
    else
        E1=learned_func(i1)-y1;//learned_func为计算输出函数（书中127页的7.105）
    /*
    When an error E is required by SMO, it will look up the error in the error cache if the 
    corresponding Lagrange multiplier is not at bound. Otherwise, it will evaluate the current
    SVM decision function based on the current alph vector.
    */
    r1=y1*E1;
    //违反KKT(Karush-Kuhn-Tucker)条件的判断
    /*
    KKT condition:
        if alphi == 0, yi*Ei >= 0;(条件1，与书上128页7.111式子对应)
        if 0 < alphi < C, yi*Ei == 0;(条件2，与书上129也7.112对应)
        if alphi == C, yi*Ei <= 0;（(条件3)，与书上129也7.113对应）
    */
    /*
    The SMO algorithm is based on the evaluation of the KKT conditions. When every multiplier 
    fulfils the KKT conditions of the problem, the algorithm terminates.
    */
    if((r1>tolerance&&alph1>0)||(r1<-tolerance&&alph1//如果找到点（xi,yi）不满足kkt条件,那么开始选择第二个点
    {
        /*使用三种方法选择第二个乘子:
        hierarchy one：在non-bound乘子中寻找maximum fabs(E1-E2)的样本
        hierarchy two：如果上面没取得进展,那么从随机位置查找non-boundary 样本
        hierarchy three：如果上面也失败，则从随机位置查找整个样本,改为bound样本
        */
        if (examineFirstChoice(i1,E1))//
        {
            return 1;
        }
        /*
        The hierarchy of second choice heuristics consists of the following:
        (A)If the above heuristic, i.e. examineFirstChoice(i1,E1), does not make positive progress, 
        then SMO starts iterating through the non-bound examples, searching for a second example that
        can make positive progress;
        (B)If none of the non-bound examples make positive progress, then SMO starts iterating through
        the entire training set until an example is found that makes positive progress.
            Both the iteration through the non-bound examples (A) and the iteration through the entire 
        training set (B) are started at random locations in order not to bias SMO towards the examples at
        the beginning of the training set.
        */
        if (examineNonBound(i1))//hierarchy two，遍历整个支持向量点
        {
            return 1;
        }

        if (examineBound(i1))//hierarchy three，随机位置遍历整个样本
        {
            return 1;
        }
        /*
        Once a first Lagrange multiplier is chosen, SMO chooses the second Lagrange
        multiplier to maximize the size of the step taken during joint optimization.
        SMO approximates the step size by |E1-E2|.
        */
    }
    ///没有进展
    return 0;
}

//hierarchy one：在non-bound乘子中寻找maximum fabs(E1-E2)的样本
//There are cases when there is no positive progress; for instance when both input vectors are identical,
//which causes the objective function to become flat along the direction of optimiztion.
int examineFirstChoice(int i1,double E1)
{
   int k,i2;
   double tmax;
   double E2,temp;
   for(i2=-1,tmax=0.0,k=0;k//end_support_i
   {
       if(alph[k]>0&&alph[k]//在间隔边界即支持向量上寻找满足条件的第二个点。
       {
           E2=error_cache[k];
           /*
           A cached error value E is kept for every non-bound training example from 
           which example can be chosed for maximizing the step size.
           */
           temp=fabs(E1-E2);//fabs:returns the absolute value of its argument.
           if(temp>tmax)
           {
               tmax=temp;
               i2=k;
           }
       }
   }

   if(i2>=0)// //如果找到了这样一个值
   {
       if(takeStep(i1,i2))//If there has a positive progress, return 1.
       {
           return 1;
       }
   }
   return 0;
}
//hierarchy two：如果上面没取得进展,那么从随机位置查找non-boundary 样本
int examineNonBound(int i1)
{
     int k;
     int k0 = rand()%end_support_i;
     //The result of the modulus operator (%) is the remainder when the first operand is divided by the second. 

     //If there is no positive progress in hierarchy one, hierarchy two will iterate through the 
     //non-bound example starting at a random position.
     int i2;
     for (k = 0; k < end_support_i; k++)
     {
         i2 = (k + k0) % end_support_i;//从随机位开始
         if (alph[i2] > 0.0 && alph[i2] < C)//查找non-bound样本
         {
             if (takeStep(i1, i2))//As soon as there has positive progress, return 1.
             {
                 return 1;
             }
         }
     }
     return 0;
}
//hierarchy three：如果上面也失败，则从随机位置查找整个样本,(改为bound样本)
int examineBound(int i1)
{
     int k;
     int k0 = rand()%end_support_i;
     //If none of the non-bound example make positive progress, then hierarchy three starts at a random
     //position in the entire training set and iterates through the entire set in finding the alph2 that
     //will make positive progress in joint optimization.
     int i2;
     for (k = 0; k < end_support_i; k++)
     {
         i2 = (k + k0) % end_support_i;//从随机位开始
         //if (alph[i2]= 0.0 || alph[i2]=C)//修改****************************************************
         {
             if (takeStep(i1, i2))//As soon as there has positive progress, return 1.
             {
                 return 1;
             }
         }
     }
     return 0;  
}
//takeStep()
//用于优化两个乘子，是否有改进，有改进，返回1，否则，返回0
//At every step, SMO chooses two Lagrange multipliers to jointly(共同地) optimize, 
//finds the optimal values for these multipliers, and updates the SVM to
//reflect the new optimal values.
int takeStep(int i1,int i2)
{
    int y1,y2,s;
    double alph1,alph2;//两个乘子的旧值
    double a1,a2;//两个乘子的新值
    double k11,k22,k12;
    double E1,E2,L,H,eta,Lobj,Hobj,delta_b;

    if(i1==i2) 
        return 0;//当两个样本相同，不进行优化。
    //给变量赋值
    alph1=alph[i1];
    alph2=alph[i2];
    y1=target[i1];
    y2=target[i2];
    if(alph1>0&&alph1else
        E1=learned_func(i1)-y1;//learned_func(int)为非线性的评价函数，即输出函数
    if(alph2>0&&alph2else
        E2=learned_func(i2)-y2;
    s=y1*y2;

    //开始计算乘子的上下限，对应与书上126页。
    //y1或y2的取值为1或-1(Binary Case)
    if(y1==y2)
    {
        double gamma=alph1+alph2;
        if(gamma>C)
        {
            L=gamma-C;
            H=C;
        }
        else
        {
            L=0;
            H=gamma;
        }
    }
    else
    {
        double gamma=alph1-alph2;
        if(gamma>0)
        {
            L=0;
            H=C-gamma;
        }
        else
        {
            L=-gamma;
            H=C;
        }
    }//计算乘子的上下限
    if(fabs(L-H) < eps)//L equals H
    {
        return 0;
    }
    //计算eta（eta为127页中7.107式子，该式子和原式子差一个-号）
    k11=kernel_func(i1,i1);//kernel_func(int,int)为核函数
    k22=kernel_func(i2,i2);
    k12=kernel_func(i1,i2);
    eta=2*k12-k11-k22;//eta是<=0的，与书上的式子插一个负号。
    if(eta<0)
    {
        a2=alph2-y2*(E1-E2)/eta;//计算新的alph2
        //调整a2，使其处于可行域
        if(a2if(a2>H)
        {
            a2=H;
        }
    }
    else//通过观察，7.107式子可以发现这里的eta必须是小于等于0的，程序运行到这个条件表明：两个样本值是相同的
        //在这种情况下，我们需要在两个端点L和H处计算目标函数，同时设置第二个乘子为使目标函数增大的值，目标函数为
        //obj=eta*a2^2/2 + (y2*(E1-E2)-eta*alph2)*a2+const,这里的公式应该是从125页7.101来的
    {
        double c1=eta/2;
        double c2=y2*(E1-E2)-eta*alph2;
        Lobj=c1*L*L+c2*L;
        Hobj=c1*H*H+c2*H;
        if(Lobj>Hobj+eps)//eps==1e-3，是一个近似0的小数。
            a2=L;
        else if(Lobjelse
            a2=alph2;//加eps的目的在于，使得Lobj与Hobj尽量分开，如果，很接近，就认为没有改进(make progress)
    }

    if(fabs(a2-alph2)//判断是否改进了a2,没有改进那么直接返回
    {
        return 0;
    }
    /***********************************
    计算新的a1
    ***********************************/
    a1=alph1-s*(a2-alph2);//根据7.109
    if(a1<0)//调整a1,使其符合条件7.103
    {
        a2+=s*a1;//这里的修改依据为公式7.102，即a1*y1+a2*y2=const value;
        a1=0;//取边界点
    }
    else if(a1>C)
    {
        double t=a1-C;
        a2+=s*t;//同上
        a1=C;
    }
    //更新阀值b
    //After each step, b is re-computed.
    {
        double b1,b2,bnew;
        if(a1>0&&a1//根据kkt条件，得出当前点落在间隔边界上。
        {
            bnew=b+E1 + y1*(a1-alph1)*k11 + y2*(a2-alph2)*k12;//根据公式7.115

        }
        else
        {
            if(a2>0&&a2//同上，根据公式7.116
            else
            {
                b1=b+E1+y1*(a1-alph1)*k11+y2*(a2-alph2)*k12;
                b2=b+E2+y1*(a1-alph1)*k12+y2*(a2-alph2)*k22;
                bnew=(b1+b2)/2;
                //When both new Lagrange multipliers are at bound and if L is not equal to H, 
                //then the interval between b1 and b2 are all thresholds that are consistent with
                //the KKT conditions. In this case, SMO chooses the threshold to be halfway in between
                //b1 and b2.
            }
        }
        delta_b=bnew-b;//更新了多少值
        b=bnew;
    }


    //更新error_cache，对取得进展的a1,a2,所对应的i1,i2的error_cache[i1]=error_cache[i2]=0
    {
        double t1=y1*(a1-alph1);
        double t2=y2*(a2-alph2);
        for(int i=0;iif(0/*
                Whenever a joint optimization occurs, the cached errors for all non-bound
                multipliers alph[i] that are not involved in the optimization are updated.
                */
                error_cache[i]+=t1*kernel_func(i1,i)+t2*(kernel_func(i2,i))-delta_b;//更新变化的值，减少运算量，依据7.117
            }
        }
        error_cache[i1]=0.0;
        error_cache[i2]=0.0;
        /*
        When a Lagrange multiplier is non-bound and is unvolved in a joint optimization,
        its cached error is set to zero.
        */
    }
    alph[i1]=a1;//store a1 in the alpha array
    alph[i2]=a2;//store a2 in the alpha array
    return 1;//说明已经取得进展
}

//learned_func(int)
//评价分类学习函数（统计学习方法中127页，7.104式子）
double learned_func(int k)
{
    double s=0.0;
    for(int i=0;iif(alph[i]>0)//alph[i]是属于[0, C]的。此行可省略。
        {
            s+=alph[i]*target[i]*kernel_func(i,k);
        }
    }
    s-=b;
    return s;
}
//计算点积函数dot_product_func(int,int)
double dot_product_func(int i1,int i2)
{
    double dot=0;
    for(int i=0;ireturn dot;
}
//The kernel_func(int, int) is RBF(Radial-Basis Function).
//K(Xi, Xj)=exp(-||Xi-Xj||^2/(2*sigma^2))
double kernel_func(int i1,int i2)
{
    double s=dot_product_func(i1,i2);
    s*=-2;
    //s+=precomputed_self_dot_product[i1]+precomputed_self_dot_product[i2];//应用余弦定理
    s+=dot_product_func(i1,i1)+dot_product_func(i2,i2);
    return exp(-s/two_sigma_squared);
}
//初始化initialize()
void initialize()
{
    int i;
    //初始化阀值b为0
    b=0.0;
    //初始化alph[]为0，要知道SMO算法就是用来求最优alph的，这里是赋初值。
    for(i=0;i0.0;
    }
    //设置样本值矩阵
    setX();//样本中的x值设置
    //设置目标值向量
    setT();//样本中的y值进行设置
    //设置预计算点积
    /*
    for(i=0;i
}
//计算误差率error_rate()
double error_rate()
{   
    ofstream to("smo_test.txt");
    int tp=0,tn=0,fp=0,fn=0;
    double ming=0,te=0,total_q=0,temp=0;
    for(int i=first_test_i;iif(temp>0&&target[i]>0)
            tp++;
        else if(temp>0&&target[i]<0)
            fp++;
        else if(temp<0&&target[i]>0)
            fn++;
        else if(temp<0&&target[i]<0)
            tn++;
        to<"  实际输出"<double)(tp+tn)/(double)(tp+tn+fp+fn);//总精度
    ming=(double)tp/(double)(tp+fn);
    te=(double)tp/(double)(tp+fp);
    to<<"---------------测试结果-----------------"<"tp="<"   tn="<"  fp="<"  fn="<"ming="<"  te="<"  total_q="<return (1-total_q);
}
//设置样本X[]
/*
void setX()
{
    //为了在需要时方便地检索要处理的数据，数据应保存在文件中。
    ifstream ff("17_smo.txt", ios::in);//ifstream用于从指定文件输入

    //exit program if ifstream could not open file
    if(!ff)//用!ff条件判断文件是否打开成功
    {
        cerr<<"File could not be opened!"<
void setX()
{
    //为了在需要时方便地检索要处理的数据，数据应保存在文件中。
    ifstream inClientFile("data2713_adjusted.txt", ios::in);//ifstream用于从指定文件输入

    //exit program if ifstream could not open file
    if(!inClientFile)//用!inClientFile条件判断文件是否打开成功
    {
        cerr<<"File could not be opened!"<1);//exit的作用为终止程序。
    }//end if

    int i=0,j=0;
    double a_data;//a_data为每次读到的数据, 默认为6位有效数字。
    while(inClientFile>>a_data)
    {
        dense_points[i][j]=a_data;
        j++;
        if(j==d)
        {
            j=0;
            i++;
        }
    }
    inClientFile.close();//显式关闭不再引用的文件。
}
//set targetT[]
void setT()
{
    //训练样本目标值
    for(int i=0;i<17;i++)
        target[i]=1;
    for(int i=17;i<27;i++)
        target[i]=-1;

    /*
    //测试样本目标值
    for(i=12090;i<13097;i++)
        target[i]=1;
    for(i=13097;i<14104;i++)
        target[i]=-1;
    */
}

三、参考资料

1、《统计学习方法》李航
2、这是上文中源码的来源，可以直接下载运行 http://download.csdn.net/detail/zjh4213/6014073
3、这是SMO算法提出者的原文献 http://download.csdn.net/detail/xr1064/7431317