人体动作捕捉与SMPL模型 (mocap and SMPL model)

人体动作捕捉与SMPL模型 (mocap and SMPL model)

FesianXu 2020.7.5

前言

笔者最近在做和motion capture动作捕捉相关的项目，学习了一些关于人体3D mesh模型的知识，其中以SMPL模型最为常见，笔者特在此进行笔记，希望对大家有帮助，如有谬误，请在评论区或者联系笔者指出，转载请注明出处，谢谢。

本文参考了[12]。

$\nabla$ 联系方式：
e-mail: [email protected]
QQ: 973926198
github: https://github.com/FesianXu

---

人体动作捕捉与人体3D mesh模型

人体动作捕捉（motion capture，以下简称mocap），我们在这个任务里面的目标是通过传感器（可以是RGB摄像头，深度摄像头或者光学标记，3D扫描仪）对人体的一段时间的某个动作进行捕捉，从而可以实现三维的人物建模。 注意到这里的“动作”一词有时候也可以用“姿态（pose）”一词描述， 在具体的表现形式上可以有以下若干种形式（也就是我们应该如何去表示某个动作的方法）：

1. 通过人体关节点表示，如Fig 1的第二张图所示。
2. 通过人体铰链结构表示，如Fig 1的第三张图所示。 （其中1和2我们都称之为人体姿态估计问题，其问题的关键在于对人体关节点的位置的预测，这里的位置可以是图片上的2D像素位置，也可能是3D空间位置）
3. 通过人体3D mesh表示，但是这个mesh并不包括人体的细节，比如表情，手势，脚踝的转动等，如Fig 1第四张图所示。
4. 通过人体细节3D mesh表示，这个mesh包含着人体的脸部表情，手势和脚踝转动等细节，如Fig 1第五张图所示。 （3和4的方法考虑了人体的形态特征，比如胖瘦，高矮等，因此表征能力更加丰富。）

Fig 1. 描述人体动作/姿态的若干种方法，原图出自[1]，其中的第四张图是本文需要介绍的SMPL模型，第五张图是在SMPL模型上扩展得到更多人体细节的SMPL-X模型。

现有的人体姿态估计（human pose estimation）和mocap关系密切，现有很多关于人体姿态估计的工作已经可以在较为复杂的多人环境里面对2D 人体关节点进行准确估计了，如[2,3,4]等。但是为了能够利用捕捉到的关节点对人物动作3D建模，我们光利用2D人体关节点是不足够的，因为2D关节点到3D空间点的映射是具有歧义性的（ambiguous），因此对于同样一个2D关节点，在空间上就有可能有多种映射的可能性，如Fig 2所示，除非用多视角的图像去消除这种歧义性。

Fig 2 如果不对3D模型进行约束，那么单纯的单视角图像将会存在2D到3D投影的歧义性，如最后一张图的(a)是原始的2D节点，其到3D的投影有非常多的可能性。这里的歧义性可以由一定数量的多视角图像消除，或者通过对人体姿态的先验进行降低，原图出自[5]和[6]。

然而，如果想要只是用单视角的图片去进行人体动作，我们就必须引入其他对人体3D姿态的先验知识，可以考虑引入的常见的先验知识有以下几种：

1. 可以对人体关节旋转的极限进行建模[6]，如果2D到3D投影过程中，我们能排除掉某些显然人体做不到的姿态（可以用关节与关节的角度极限表示），那么我们就去除了一定的歧义性。因此[6]作者收集了很多瑜伽表演者的人体极限姿态的角度数据集。

2. 可以收集大规模正常人体活动的3D 扫描数据，如AMASS[7]，是一个集成了15个人体真实的3D扫描数据集，并且用SMPL人体模型进行标准参数化的大型数据库，通过它，我们可以隐式地学习到人体的正常姿态，很大程度上减少歧义性，具体见HMR模型[8]，VIBE模型[8]。

现在流行的，而且效果不错的方法都是第二种方法，也就是通过建立大规模的真实人体3D数据集，这个数据集需要进行标准的参数化成数字人体模型，比如SMPL模型。然后通过对抗学习进行人体姿态正则的引入。比如HMR模型[5]，其示意图见Fig 3。

Fig 3 在HMR模型中，作者通过在大规模的真实人体mesh数据上进行对抗学习，从而引入了人体姿态正则，原图出自[5]。

不管是为了对人体3D模型进行标准化的参数化，从而建模成3D数字人体模型，还是为了对人体3D模型进行渲染，亦或是为了引入人体姿态先验知识，我们都需要想办法设计一个可以数字化表示人体的方法，SMPL模型就是其中一种最为常用的。接下来我们简要介绍下SMPL模型。

SMPL模型

SMPL模型在[9]提出，其全称是Skinned Multi-Person Linear (SMPL) Model，其意思很简单，Skinned表示这个模型不仅仅是骨架点了，其是有蒙皮的，其蒙皮通过3D mesh表示，3D mesh如Fig 4所示，指的是在立体空间里面用三个点表示一个面，可以视为是对真实几何的采样，其中采样的点越多，3D mesh就越密，建模的精确度就越高（这里的由三个点组成的面称之为三角面片），具体描述见[10]。Multi-person表示的是这个模型是可以表示不同的人的，是通用的。Linear就很容易理解了，其表示人体的不同姿态或者不同升高，胖瘦（我们都称之为形状shape）是一个线性的过程，是可以控制和解释的（线性系统是可以解释和易于控制的）。那么我们继续探索SMPL模型是怎么定义的。

Fig 4 不同解析率的兔子模型的3D mesh。

在SMPL模型中，我们的目标是对于人体的形状比如胖瘦高矮，和人体动作的姿态进行定义，为了定义一个人体的动作，我们需要对人体的每个可以活动的关节点进行参数化，当我们改变某个关节点的参数的时候，那么人体的姿态就会跟着改变，类似于BJD球关节娃娃[11]的姿态活动。为了定义人体的形状，SMPL同样定义了参数$\beta \in {\mathbb{R}}^{10}$，这个参数可以指定人体的形状指标，我们后面继续描述其细节。

Fig 5 SMPL模型定义的24个关节点及其位置。

总体来说，SMPL模型是一个统计模型，其通过两种类型的统计参数对人体进行描述，如Fig 6所示，分别有：

1. 形状参数（shape parameters）：一组形状参数有着10个维度的数值去描述一个人的形状，每一个维度的值都可以解释为人体形状的某个指标，比如高矮，胖瘦等。
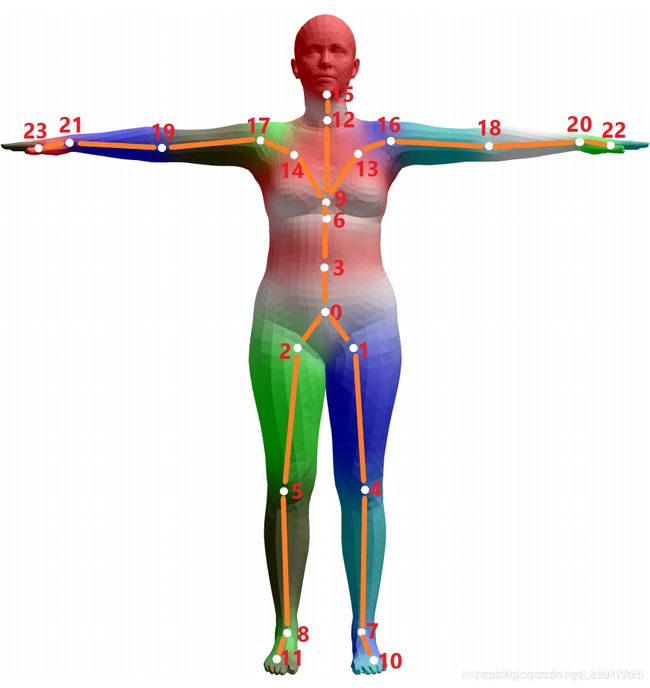
2. 姿态参数（pose parameters）：一组姿态参数有着$24\times 3$维度的数字，去描述某个时刻人体的动作姿态，其中的$24$表示的是24个定义好的人体关节点，其中的$3$并不是如同识别问题里面定义的$(x,y,z)$空间位置坐标（location），而是指的是该节点针对于其父节点的旋转角度的轴角式表达(axis-angle representation)（对于这24个节点，作者定义了一组关节点树）

Fig 6 形状参数和姿态参数，原图出自[12]。

具体的$\beta$和$\theta$变化导致的人体mesh的变化的效果图可视化，大家可以参考博文[13]和[14]。

相信看到现在，诸位读者对于这种通过若干个参数去控制整个模型的姿态，形状的方法有所了解了，我们对于一个模型的形状姿态的mesh控制，一般有两种方法，一是通过手动去拉扯模型mesh的控制点以产生mesh的形变；二是通过Blend Shape，也就是混合成形的方法，通过不同参数的线性组合去“融合”成一个mesh。

继续探索SMPL模型

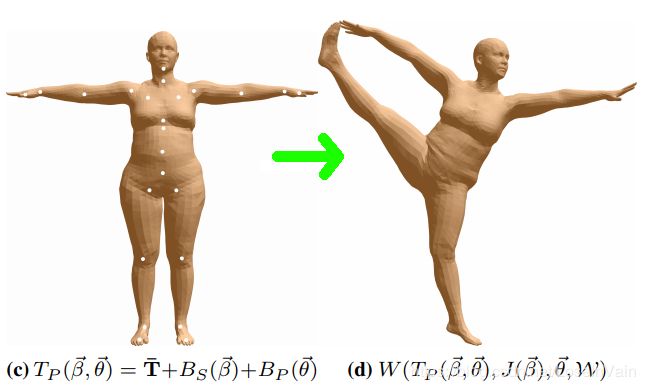
我们大致对SMPL模型和数字人体模型参数化有了个一般性的了解后，我们继续探究不同的参数对于人体模型的影响。整个从SMPL模型合成数字人体模型的过程分为三大阶段：

1. 基于形状的混合成形 （Shape Blend Shapes）：在这个阶段，一个基模版（或者称之为统计上的均值模版） $\bar{\mathbf{T}}$ 作为整个人体的基本姿态，这个基模版通过统计得到，用$N=6890$个端点(vertex)表示整个mesh，每个端点有着$(x,y,z)$三个空间坐标，我们要注意和骨骼点joint区分。

   随后通过参数$\beta$去描述我们需要的人体姿态和这个基本姿态的偏移量，叠加上去就形成了我们最终期望的人体姿态，这个过程是一个线性的过程。其中的$B_S(\beta )$就是一个对参数$\beta$的一个线性矩阵的矩阵乘法过程，我们接下来会继续讨论。此处得到的人体mesh的姿态称之为静默姿态(rest pose，也可以称之为T-pose)，因为其并没有考虑姿态参数的影响。

Fig 7 在基模版mesh上线性地叠加偏量，得到了我们期望的人体mesh。

2. 基于姿态的混合成形 (Pose Blend Shapes) ：当我们根据指定的$\beta$参数对人体mesh进行形状的指定后，我们得到了一个具有特定胖瘦，高矮的mesh。但是我们知道，特定的动作可能会影响到人体的局部的具体形状变化，举个例子，我们站立的时候可能看不出小肚子，但是坐下时，可能小肚子就会凸出来了，哈哈哈，这个就是很典型的 具体动作姿态影响人体局部mesh形状的例子了。 换句话说，就是姿态参数$\theta$也会在一定程度影响到静默姿态的mesh形状。

   

   Fig 8 人体具体的姿态对于mesh局部形状也会有细微的影响。

3. 蒙皮 (Skinning)：在之前的阶段中，我们都只是对静默姿态下的mesh进行计算，当人体骨骼点运动时，由端点(vertex)组成的“皮肤”将会随着骨骼点(joint)的运动而变化，这个过程称之为蒙皮。蒙皮过程可以认为是皮肤节点随着骨骼点的变化而产生的加权线性组合。简单来说，就是距离某个具体的骨骼点越近的端点，其跟随着该骨骼点旋转/平移等变化的影响越强。

Fig 9 综合考虑混合成形和蒙皮后的人体mesh。

附带提一句，当我们描述人体姿态和人体运动时，我们在这里的方法是计算每个关节点对于其静默模型的旋转偏差，比如对于1号节点来说，某个姿态需要旋转参数${\theta }_1$的变换后，可以从静默姿态到该姿态，当然，因为整个骨骼点是符合铰链式骨骼树的，1号节点的旋转会导致其子节点的相应变化，具体的过程就是前向动力学(Forward Kinematics)的过程了。当然，这里的旋转参数即可以是轴角式的三个参数，也可以将其转化成旋转矩阵$\mathbf{R}\in {\mathbb{R}}^{3\times 3}$。

我们接下来详细讨论下刚才提到的三个阶段。

基于形状的混合成形

SMPL模型设定的基模版$\bar{\mathbf{T}}$是通过统计大量的真实人体mesh，得到的均值形状。通过对主要形状成分(Principal Shape Components)或者称之为端点偏移(Vertex Deviations)进行线性组合，并且在基模版上进行叠加，我们就形成了静默姿态的mesh。这里指的主要形状成分指的是在数据集中统计得到的mesh的主要变化成分。具体来说，每个主成份都是一个$6890\times 3$的矩阵，其中某个$(x,y,z)$表示的是相对于对应的基模版上的端点的偏移。举个例子来说，Fig 10是第一个主成份和第二个主成份的可视化结果。

Fig 10 shape参数的第一主成份和第二主成的可视化结果，我们发现shape参数是具有可解释性的，每个维度代表着人体形状的不同维度的变化。比如视觉上来看，似乎第一个表示的是高矮，第二个表示了胖瘦。

我们可以用以下公式表示整个过程：
$${\mathbf{V}}_{shape}=\mathbf{D}\beta +\bar{\mathbf{T}}\text{\hspace{1em}(1)}$$
其中$\mathbf{D}\in {\mathbb{R}}^{6890\times 3\times 10}$是10个主成份的偏移，$\beta \in {\mathbb{R}}^{10}$表示的是10个主成份偏移的大小，$\bar{\mathbf{T}}\in {\mathbb{R}}^{6890\times 3}$表示的是基模版的mesh，${\mathbf{V}}_{shape}\in {\mathbb{R}}^{6890\times 3}$表示的是混合成形后的mesh。

在文章[9]中也用公式(2)表示这个偏移量：
$$B_S(\beta ;\mathcal{S})=\sum _{n=1}^{|\beta |}{\beta }_n{\mathbf{S}}_n\text{\hspace{1em}(2)}$$
其实就是等价于式子(1)中的$\mathbf{D}\beta$。不过这种形式的表示有一个好处就是容易分清楚这个数字人体模型的人工指定参数部分$\beta$和需要模型根据数据集去学习的参数矩阵$\mathcal{S}$，通常用分号隔开了这两类型参数，后文我们将会沿用这种表述。

基于姿态的混合成形

在SMPL模型中，如Fig 5所示，通过定义了24个关节点的层次结构，并且这个层次结构是通过运动学树（Kinematic Tree）定义的，因此保证了子节点和父节点的相对运动关系。

以0号节点为根节点，通过其他23个节点相对于其父节点（根据其运动学树结构可以定义出节点的父子关系）的旋转角度，我们可以定义出整个人体姿态的姿势。这里的旋转是用的轴角式表达的，一般来说，轴角式是一个四元组$(x,y,z,\theta )$，表示以$\mathbf{e}=(x,y,z{)}^{\mathrm{T}}$为轴，旋转$\theta$度。本文采用的是三元数表示 $\theta =(x,y,z)$，如Fig 11所示，其旋转轴为其单位向量$\mathbf{e}=\frac{\theta }{||\theta ||}$，其旋转大小是$||\theta ||$。

Fig 11 用轴角式表示旋转的方向和大小

那么表示这些非根节点的相对于父节点的相对旋转需要用$23\times 3$个参数，为了表示整个人体运动的全局旋转（也称之为朝向，Orientation）和空间位移，比如为了表示人体的行走，奔跑等，我们还需要对根节点定义出旋转和位移，那么同样的，需要用3个参数以轴角式的方式表达旋转，再用3个参数表达空间位移。

需要特别注意的是，轴角式并不方便计算，因此通常会把它转化成旋转矩阵进行计算，其参数量从3变成了$3\times 3=9$个。具体过程见Rodrigues公式。
$$\exp ({\omega }_j)=\mathcal{I}+{\hat{\bar{\omega }}}_j\sin (||{\omega }_j||)+{\hat{\bar{\omega }}}_j^2\cos (||{\omega }_j||)\text{\hspace{1em}(3)}$$
然而人体的朝向和空间位移不影响混合成形的mesh效果，因此在控制mesh成形方面，基于姿态的混合成形需要$R(\theta )=23\times 9=207$个基本的pose模版，其中函数$R(\cdot )$表示的是有正弦函数和余弦函数组合成的函数，其将轴角式表达成旋转矩阵，可知道其对于$\theta$而言是非线性的。因此，为了考虑到pose导致的混合成形的影响，我们需要对这207个旋转相关参数进行学习训练，得到矩阵$\mathcal{P}=[{\mathbf{P}}_1,\cdots ,{\mathbf{P}}_{9K}]\in {\mathbb{R}}^{3N\times 9K}$，其中的$K=23,N=6890$。这个矩阵是需要算法根据数据集学习的，类似于式子(2)中的$\mathcal{S}$。因此，如果考虑到和静默姿态之间的差别，在对其进行差异转换到mesh端点上，我们得出以下式子进行基于姿态的混合成形：
$$B_P(\theta ;\mathcal{P})=\sum _{n=1}^{9K}(R_n(\theta )-R_n({\theta }^{\ast })){\mathbf{P}}_n\text{\hspace{1em}(4)}$$
其中的混合基底形状${\mathbf{P}}_n\in {\mathbb{R}}^{3N}$是一个表征当前期望姿态和静默姿态之间的差别的矩阵。

至此，我们对人体模型的mesh进行了基于形状和姿态的混合成形，文章[12]提供了伪代码实现，我这里贴出来下：

# self.pose :   24x3    the pose parameter of the human subject
# self.R    :   24x3x3  the rotation matrices calculated from the pose parameter
pose_cube = self.pose.reshape((-1, 1, 3))
self.R = self.rodrigues(pose_cube)

# I_cube    :   23x3x3  the rotation matrices of the rest pose
# lrotmin   :   207x1   the relative rotation values between the current pose and the rest pose   
I_cube = np.broadcast_to(
      np.expand_dims(np.eye(3), axis=0),
      (self.R.shape[0]-1, 3, 3)
    )
lrotmin = (self.R[1:] - I_cube).ravel()

# v_posed   :   6890x3  the blended deformation calculated from the
v_posed = v_shaped + self.posedirs.dot(lrotmin)

骨骼点位置估计

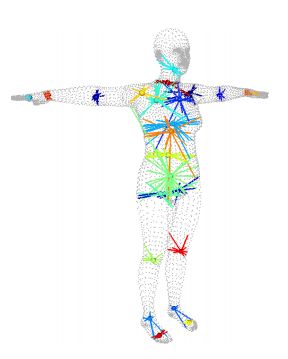
因为不同人体形状具有较大差异性，因此在经过了之前谈到的两种混合成形之后，我们仍然需要根据成形后的mesh估计出符合该mesh的骨骼点，以便于我们后续对这些骨骼点进行旋转，形成我们最终期望的姿态。因此，骨骼点位置估计（Joint Locations Estimation）在这里指的是根据混合成形后静默姿态下的mesh端点的位置，估算出静默姿态的作为控制点的骨骼点的理想位置。整个过程通过式子(5)操作。其中的$\mathcal{J}\in {\mathbb{R}}^{(K+1)\times N}$是变换矩阵，也是通过数据集上学习训练得到，其中的$K+1=24,N=6890$。 $\bar{\mathbf{T}}+B_P(\beta ;\mathcal{S})\in {\mathbb{R}}^{N\times 3}$其实就是经过基于形状混合成形后的mesh端点。那么我们最终的$J(\beta ;\mathcal{J},\bar{\mathbf{T}},\mathcal{S})\in {\mathbb{R}}^{(K+1)\times 3}$。整个过程可以可视化成Fig 12所示，每个骨骼点的位置由它本身最为接近的若干个mesh的端点加权决定。

$$J(\beta ;\mathcal{J},\bar{\mathbf{T}},\mathcal{S})=\mathcal{J}(\bar{\mathbf{T}}+B_P(\beta ;\mathcal{S}))\text{\hspace{1em}(5)}$$

Fig 12 通过mesh的端点去估计作为操作点的骨骼点的空间位置。

蒙皮

在经过骨骼点位置估计之后，我们便有了对整个人体数字模型进行操作的控制点了，其实就是骨骼点。当我们对骨骼点进行旋转时，我们可以像摆动球形关节娃娃一样将静默姿态下的人体摆成我们需要的姿态。人体mesh端点也会随着其周围的关节点一起变化，形成我们最后看到的人体数字模型。因此蒙皮其实是让静默姿态下的人体骨架“动起来”，并且对其蒙上“皮肤”的过程。

Fig 13 对静默姿态下的骨骼点进行相应的旋转后，得到期望的人体姿态，相应的，骨骼点周围的mesh端点也会随之移动，形成我们最终看到的人体数字模型效果。

Reference

[1]. Pavlakos G, Choutas V, Ghorbani N, et al. Expressive body capture: 3d hands, face, and body from a single image[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019: 10975-10985.

[2]. Cao Z , Hidalgo G , Simon T , et al. OpenPose: Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018.

[3]. Fang H S, Xie S, Tai Y W, et al. Rmpe: Regional multi-person pose estimation[C]//Proceedings of the IEEE International Conference on Computer Vision. 2017: 2334-2343.

[4]. Chen Y, Wang Z, Peng Y, et al. Cascaded pyramid network for multi-person pose estimation[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 7103-7112.

[5]. Kanazawa A, Black M J, Jacobs D W, et al. End-to-end recovery of human shape and pose[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 7122-7131.

[6]. Akhter I, Black M J. Pose-conditioned joint angle limits for 3D human pose reconstruction[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 1446-1455.

[7]. Mahmood N, Ghorbani N, Troje N F, et al. AMASS: Archive of motion capture as surface shapes[C]//Proceedings of the IEEE International Conference on Computer Vision. 2019: 5442-5451.

[8]. Kocabas M, Athanasiou N, Black M J. VIBE: Video inference for human body pose and shape estimation[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020: 5253-5263.

[9]. Loper M, Mahmood N, Romero J, et al. SMPL: A skinned multi-person linear model[J]. ACM transactions on graphics (TOG), 2015, 34(6): 1-16.

[10]. https://whatis.techtarget.com/definition/3D-mesh

[11]. https://baike.baidu.com/item/BJD%E5%A8%83%E5%A8%83/760152?fr=aladdin

[12]. https://khanhha.github.io/posts/SMPL-model-introduction/

[13]. https://www.cnblogs.com/xiaoniu-666/p/12207301.html

[14]. https://blog.csdn.net/chenguowen21/article/details/82793994