MVG学习笔记(1) --无处不在的射影几何

前言

  关于计算机视觉圣经的学习笔记。本次此系列的博文除了本次博文，基本不会包含前言了，参考书《多视图几何》第二版。

无处不在的射影几何

  我们熟悉射影变换,比如看图像,方不是方,圆并非圆.将二维对象映射成图片是射影变换的例子。

  射影变换保留了哪些属性?值得肯定的是,形状必定没有保留,所以圆可能是表现为椭圆。也不会是长度，因为通过射影变换，两个垂直的圆半径被不同的量拉伸。

  角度，距离，距离比 - 这些都不会被保留，并且可能看起来通过射影变换保留非常小的几何。

  但是，保留的属性是直线性(straightness)。

  事实证明，这是对映射的最一般要求，并且我们可以将平面的射影变换定义为保持直线的平面上的点的任何映射。

  为了了解我们为什么需要射影几何，我们从熟悉的欧几里德几何开始。

  欧几里德几何描述对象的角度和形状的几何学科。 欧几里德几何在一个主要方面是令人苦恼的- 我们需要不断推理几何的几个基本概念 - 例如线的相交。

  两条线（我们在这里考虑的是二维几何）几乎总是在一个点上相交，但是有一些线不能这样做 - 那些我们称之为平行线。

  解决这个问题的一个常见说法就是平行线相交于“无穷远”的点。

  然而，这并不完全令人信服，并且与另一个说法相冲突，即无穷（无限）是不存在的，并且只是一个方便的虚构。

  我们可以通过增加平行线相交于无穷远处的这些点来增强欧几里得平面，并通过将它们称为“理想点”来解决无穷大的难度。

  通过在无穷远处添加这些点，熟悉的欧几里德空间被转换为一种新型的几何对象，射影空间。 这是一种非常有用的思维方式，因为我们熟悉欧氏空间的属性，涉及距离，角度，点，线和入射角(incidence)等概念。 射影空间没有什么神秘之处 - 它只是欧几里德空间的延伸，其中两条线总是在一个点上相遇，尽管有时在无穷远处的神秘点处。

坐标

  欧几里得二维空间中的一个点由有序的实数对$(x,y)$表示。我们可以为这一对添加一个额外的坐标，给出一个三元组$(x,y,1)$，我们声明它们代表相同的点。这似乎无害，因为我们可以通过添加或删除最后一个坐标，从该点的一个表示返回前进到另一个表示。

  我们现在采取重要的概念步骤，询问为什么最后一个坐标需要为1 - 毕竟，其他两个坐标不是那么受约束。坐标三元组$(x,y,2)$怎么样？在这里，我们做出一个定义，并说$(x,y,1)$和$(2x,2y,2)$代表相同的点，而且，$(kx,ky,k)$也代表相同的点，其中是对于任何非零值$k$均成立。形式上，点由坐标三元组的等价类表示，其中两个三元组在它们相差一个共同倍数时是等价的。这些被称为点的齐次坐标。给定坐标三元组$(kx,ky,k)$，我们可以通过除以k得到原始坐标得到$(x,y)$。

  读者将观察到虽然$(x,y,1)$表示与坐标对$(x,y)$相同的点，但没有对应于三元组$(x,y,0)$的点。 如果我们试图除以最后一个坐标，我们得到无限的点$(x/0,y/0)$, 这就是无穷远点。 它们是由齐次坐标表示的点，其中最后一个坐标为零。

  一旦我们看到如何为二维欧几里德空间做到这一点，通过将点表示为齐次向量将其扩展到射影空间，很明显我们可以在任何维度上做同样的事情。 通过将点表示为齐次向量，欧几里德空间${\mathrm{I}\mathrm{R}}^n$可以扩展到射影空间${\mathrm{I}\mathrm{P}}^n$。 事实证明，二维射影空间中无穷远处的点形成一条线，通常称为无穷远处的线。 在三维空间中，它们形成无限远的平面。

齐次性

  在经典的欧几里德几何中，所有点都是相同的。 没有区别。

  整个空间是齐次的。 添加坐标时，似乎选择了一个点作为原点。 但是，重要的是要意识到这只是所选择的特定坐标系的意外。 我们也可以找到一种不同的方法来坐标化平面，其中不同的点被认为是原点。 实际上，我们可以考虑改变欧几里德空间的坐标，其中轴被平移并旋转到不同的位置。 我们可能会以另一种方式想到这一点，因为空间本身会平移并旋转到不同的位置。 产生的操作称为欧几里德变换。

  更一般的变换类型是将线性变换应用于${\mathrm{I}\mathrm{R}}^n$，然后通过欧几里德变换平移空间原点。 我们可以将其视为空间移动，旋转并最终可能通过不同方向的不同比率线性拉伸。 产生的变换称为仿射变换。

  欧几里德或仿射变换的结果是无穷远处的点保持在无穷远处。 通过这种变换，这些点以某种方式保留，至少作为一组。 它们在某种程度上是区分的，或者在欧几里德或仿射几何的背景下是特殊的。

  从射影几何的角度来看，无穷远处的点与其他点没有任何不同。就像欧几里德空间是一致的一样，投射空间也是如此。点的无穷大属性在齐次坐标表示中即最后一个坐标为零，只不过是坐标系选择的原因。通过类比欧几里德或仿射变换，我们可以定义射影空间的射影变换。欧几里德空间${\mathrm{I}\mathrm{R}}^n$的线性变换由应用于该点坐标的矩阵乘法表示。以相同的方式，射影空间${\mathrm{I}\mathrm{P}}^n$的射影变换是表示点$\mathrm{a}\mathrm{n}(n+1)$- 矢量的齐次坐标的映射，其中坐标矢量乘以非奇异矩阵。在这种映射下，无穷远处的点（最后一维坐标为零）被映射到任意其他点。无穷远处的点不会被保留。因此，射影空间${\mathrm{I}\mathrm{P}}^n$的射影变换由齐次坐标的线性变换表示.

$$X^{\prime }=H_{(n+1)\times (n+1)}X$$

  在计算机视觉问题中,通过将其扩展到三维（3D）射影空间，使得射影空间被用作表示真实3D世界的便利方式。类似地，通常通过将世界射影到二维表示上而形成的图像为了方便而扩展为被认为位于二维射影空间中。实际上，现实世界及其图像不包含无穷远处的点，我们需要将手指放在虚拟点上，即图像中无穷远处的线和世界上无限远处的平面。出于这个原因，虽然我们通常使用射影空间，但我们知道无穷远处的直线和平面在某种程度上是特殊的。这违背了纯射影几何的精神，但却使我们的实际问题变得有用。一般来说，我们试图通过将射影空间中的所有点视为对我们来说是平等的，并且在必要时,在空间中的无限远处或图像中无穷远处的平面中单独划出它。

仿射和欧几里得几何

  我们已经看到，通过在无穷远处添加线（或平面）可以从欧几里得空间获得射影空间。 我们现在考虑倒退的相反过程。 本讨论主要涉及二维和三维射影空间。

仿射几何

  我们将认为射影空间的点最初是齐次的，没有特定的坐标系是优选的。在这样的空间中，没有线的平行的概念，因为平行线（或三维情况中的平面）是在无限远处相交的线。 然而，在射影空间中，没有关于点在无穷远处的概念 - 所有点都是相等的。 我们说平行不是射影几何的概念。 谈论它毫无意义。

  为了使这样的概念有意义，我们需要选择一些特定的线，并确定这是无穷远处的线。这导致这样的情况：尽管所有点都是相等的，但是有些点比其他点更相等。

  因此，从一张白纸开始，并想象它延伸到无限并形成投射空间${\mathrm{I}\mathrm{P}}^2$。我们所看到的只是空间的一小部分，看起来很像普通的欧几里德平面。

  现在，让我们在纸上画一条直线，并声明这是无穷远处的线。

  接下来，我们绘制另外两条在此显著的线上相交。

  由于它们在“无穷远线”处相交，我们将它们定义为平行。

  这种情况类似于通过观察无穷远平面所看到的情况。想想在地球非常平坦的地方拍摄的照片。平面中无穷远处的点在图像中显示为地平线。诸如铁路轨道之类的线条在图像中显示为在地平线处会合的线条。位于地平线上方的图像中的点（天空图像）显然与世界平面上的点不对应。

  但是，如果我们考虑将相应的光线向后延伸到相机后面，它将与平面相交在相机后面的某个点。因此，图像中的点与世界平面中的点之间存在一对一的关系。

  世界平面中无穷远处的点对应于图像中的真实水平线，并且世界中的平行线对应于在地平线处会合的线。

  从我们的观点来看，世界平面及其图像只是观察射影平面几何形状的另一种方式，加上一条显着的线条。

  射影平面的几何形状和区分线被称为仿射几何，并且将一个空间中的区分线映射到另一个空间的区分线的任何射影变换被称为仿射变换。。

  通过将特殊线识别为“无穷远线”，我们能够定义平面中直线的平行。 但是，只要我们可以定义平行，某些其他概念也是有意义的。 例如，我们可以定义平行线上两点之间的间隔的等式。

  例如，如果A，B，C和D是点，并且线AB和CD是平行的，那么如果线AC和BD也是平行的，则我们将两个间隔AB和CD定义为具有相等的长度。 类似地，如果在平行线上存在等于两者的另一个间隔，则同一线上的两个间隔是相等的。

  你可以想象这是平行四边形

欧几里得几何

  通过区分射影平面中的特殊线，我们获得了平行的概念和它的仿射几何。 仿射几何被视为射影几何的特化，其中我们挑出一条特定的线（或根据尺寸的平面）并将其称为无穷远处的线。

  接下来，我们转向欧几里德几何，并表明通过在仿射几何无穷远中挑出线或平面的一些特殊特征变为欧几里德几何。 在这样做的过程中，我们介绍了最重要的概念之一，即绝对的二次曲线曲线(absolute conic)。

  我们首先考虑二维几何，然后从圆开始。 请注意，圆不是仿射几何的概念，因为平面的任意拉伸（将线保持在无穷远处）将圆转变为椭圆。 因此，仿射几何不区分圆和椭圆。

  然而，在欧几里德几何中，它们是截然不同的，并且具有重要的区别。 代数的情况下，椭圆由二次方程描述。 因此，预期并且确实两个椭圆最通常在四个点相交。 然而，几何上显而易见的是，两个不同的圆不能在两个以上的点上相交。 在代数上，我们在这里求这两个二次曲线相交，或者等价地求解两个二次方程。 我们应该期望获得四种解决方案。 问题是，圆的特殊之处在于它们只在两点相交。

  这个问题的答案当然是存在另外两个解决方案，两个圆在另外两个复数点(complex points)上相交。 我们不必看很远就能找到这两点。

  齐次坐标$(x，y，w)$中的圆的等式是该形式

$$(x-aw{)}^2+(y-bw{)}^2=r^2{w}^2$$

  这表示具有以齐次坐标表示的中心的圆$(x_0,y_0,w_0{)}^T=(a,b,1{)}^T$。 很快证实点$(x,y,w{)}^T=(1,\pm i,0{)}^T$位于每个这样的圆上。

$1+i^2=0,是必然$

  为了重复这个有趣的事实，每个圆都通过点$(1,\pm i,0{)}^T$，因此它们位于任意两个圆的交点。 由于它们的最终坐标为零，因此这两个点位于无穷远处。

  由于显而易见的原因，它们被称为平面的圆形点(虚圆点,circular points)。 注意，尽管两个圆点是复杂的，但它们满足一对实方程：$x^2+y^2=0;w=0$。

  这个观察结果给出了我们如何定义欧氏几何的线索。 欧几里德几何来自射影几何，首先在无穷远处挑出一条直线，然后在这条线上的两个点称为虚圆点。 当然，虚圆点是复杂的点，但在大多数情况下，我们并不担心这一点。

  现在，我们可以将圆定义为通过两个虚圆点的任何二次曲线（由二次方程定义的曲线）。 注意，在标准欧几里得坐标系中，虚圆点具有坐标$(1,\pm i,0{)}^T$。 然而，在将欧几里德结构分配给射影平面时，我们可以将该线上的任何线和任何两个（复杂）点分别指定为无穷远处的线和虚圆点。

  作为应用该观点的一个例子，我们注意到可以发现通过平面中的五个任意点的一般圆锥，如通过计算一般二次方程$a{x}^2+b{y}^2+...+f{w}^2=0$的系数的数量可以看出的。另一方面，圆仅由三个点定义。

  另一种看待它的方法是它是一个通过两个特殊点的圆锥曲线，即虚圆点，以及其他三个点，因此与任何其他圆锥一样，它需要五个点来唯一地指定它。

  由于挑出两个圆点，人们可以获得整个熟悉的欧氏几何形状，这一点不足为奇。 特别地，诸如角度和长度比的概念可以根据虚圆点来定义。 然而，这些概念最容易根据欧几里得平面的某些坐标系来定义，这将在后面的章节中看到。

3D欧几里得几何

  我们通过在无穷远处指定一条线和一对虚圆点来看到欧几里得平面是如何用射影平面定义的。 相同的想法可以应用于3D几何。

  在二维情况下，可以仔细观察球体以及它们如何相交。 两个球体相交成圆形，而不是像一般的四度曲线那样，如代数所暗示的那样，是两个一般的椭圆体（或其他二次曲面）。

  这一思路导致发现在齐次坐标$(\mathrm{X},\mathrm{Y},\mathrm{Z},\mathrm{T}{)}^{\mathrm{T}}$中，所有球体在无穷远处与平面相交，其方程为：${\mathrm{X}}^2+{\mathrm{Y}}^2+{\mathrm{Z}}^2=0;\mathrm{T}=0$。这是位于无穷远平面上的二度曲线（圆锥曲线,a conic），仅由复杂点组成。 它被称为绝对二次曲线(absolute conic)，是关键几何实体之一，尤其是因为它与相机校准相关联，这将在后面看到。

  绝对二次曲线仅由欧几里德坐标系中的上述方程定义。 一般来说，我们可以认为3D欧几里德空间是通过将特定平面挑选为无限平面并指定位于该平面中的特定二次曲线作为绝对二次曲线而从射影空间导出的。 这些实体可以在射影空间的坐标系方面具有非常一般的描述。

  我们在此不会详细介绍绝对二次曲线如何确定完整的欧几里德三维几何。一个例子就可以了。

  空间中直线的垂直不是仿射几何中的有效概念，而是属于欧几里德几何。线的垂直可以用绝对二次曲线来定义，如下所述。

  通过延伸线直到它们与无穷远处的平面相交，我们得到两个点，称为两条线的方向。线的垂直根据两个方向与绝对二次曲线的关系来定义。如果两个方向是相对于绝对二次曲线的共轭点，则线是垂直的。

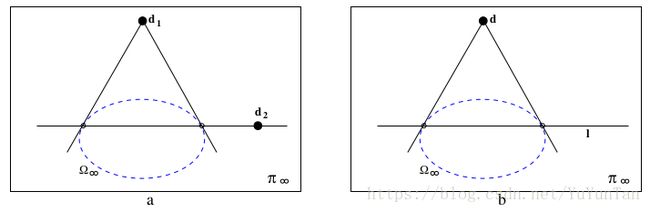
  共轭点的几何和代数表示在以后会讲，想提前明白请百度。简而言之，如果绝对二次曲线由3×3对称矩阵${\Omega }_{\infty }$表示，并且方向是点$d_1$和$d_2$，则如果相对于${\Omega }_{\infty }$共轭则有$d_1^T{\Omega }_{\infty }{d}_2=0$。更一般地，角度可以根据任意坐标系中的绝对二次曲线来定义，如下所表示的。

$$\cos \theta \frac{(d_1^T{\Omega }_{\infty }{d}_2)}{\sqrt{(d_1^T{\Omega }_{\infty }{d}_1)(d_2^T{\Omega }_{\infty }{d}_2)}}$$