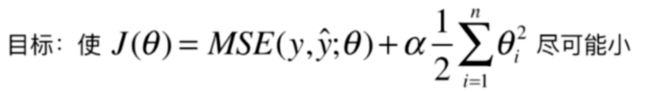机器学习 -- 多项式回归（Ⅶ 岭回归 Ridge Regression）

岭回归Ridge Regression（模型正则化的方式之一）

      

编程实现岭回归：

（1）导入数据集

import numpy as np
import matplotlib.pyplot as plt

# 模型样本
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)

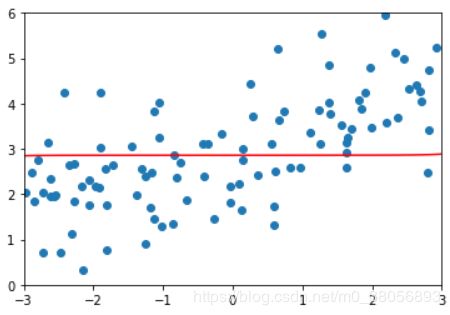
# 绘制样本曲线
plt.scatter(x, y)
plt.show()

（2）定义一个根据模型绘图的函数

# 定义绘图模型
def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)

    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])

（3）使用多项式回归对样本进行训练

from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error


# 定义多项式回归函数
def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])


# 分割数据集
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)



# 多项式回归对样本进行训练，使用20个维度
poly20_reg = PolynomialRegression(20)
poly20_reg.fit(X_train, y_train)

y20_predict = poly20_reg.predict(X_test)
mean_squared_error(y_test, y20_predict)
# 167.9401085999025

发现均方误差非常大，打印图像如下，发现拟合的曲线出现了过拟合的问题，两段有极端的情况。

plot_model(poly20_reg)

（4）以下使用岭回归进行训练

from sklearn.linear_model import Ridge

def RidgeRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("ridge_reg", Ridge(alpha=alpha))
    ])

# 注意alpha后面的参数是所有theta的平方和，而对于多项式回归来说，岭回归之前得到的θ都非常大
# 所以为了限制让他们比较小，我们前面系数可以取的小一些
ridge1_reg = RidgeRegression(degree=20, alpha=0.00001)
ridge1_reg.fit(X_train, y_train)
ridge1_predict = ridge1_reg.predict(X_test)
mean_squared_error(y_test ,ridge1_predict)
# 1.3874378026530747

plot_module(ridge1_reg)

发现通过使用岭回归，我们的均方误差小了非常多，曲线也缓和了许多。

 

alpha值的影响

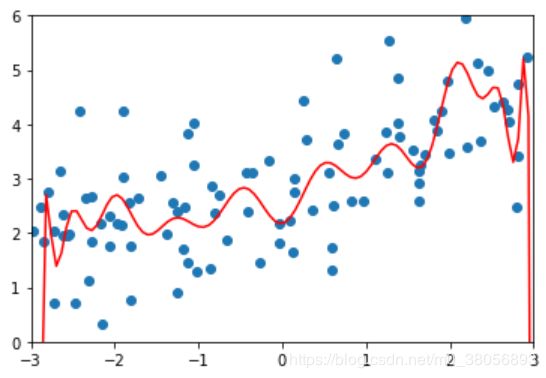
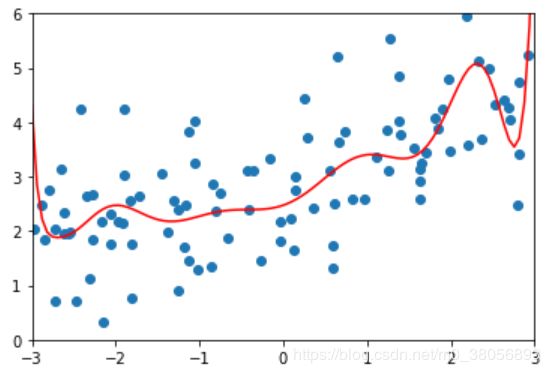
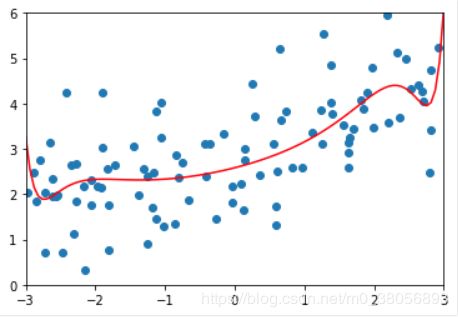
        修改alpha值，分别为1,100,100000（如下图从上到下）。可以看出线条逐渐变得平滑，当alpha很大的时候，为了使目标函数小，所以会使系数趋近于0，因此会得出几乎平行的一条直线。

 

         当alpha非常大的时候，我们的模型实际上相当于就是在优化θ的平方和这一项，使得其最小（因为MSE的部分相对非常小）。而使得θ的平方和最小，就是使得每一个θ都趋近于0，这个时候曲线就趋近于一根直线了。