SVM支持向量机系列理论（四） 软间隔支持向量机

4.1 软间隔SVM的经典问题

对于线性可分的数据集，可以使用线性可分支持向量机的方法，找出最优间隔的分离超平面。线性可分支持向量机的经典问题为：

min w,b  12||w||2 m i n   w , b     1 2 | | w | | 2

                                    
s.t.   yi(w⋅xi+b)≥1;    (i=1,...,N)          s . t .       y i ( w ⋅ x i + b ) ≥ 1 ;         ( i = 1 , . . . , N )                  

但是，在实际应用中，我们数据集因为存在一些数据点使得数据集不是完全线性可分的。因此，引入了软间隔的SVM支持向量机。

min w,b,e  12||w||2+C∑Ni=1ξi m i n   w , b , e     1 2 | | w | | 2 + C ∑ i = 1 N ξ i

                                    
s.t.   yi(w⋅xi+b)≥1−ξi; s . t .       y i ( w ⋅ x i + b ) ≥ 1 − ξ i ;

                       ξi≥0;(i=1,...,N)             (1)                                               ξ i ≥ 0 ; ( i = 1 , . . . , N )                           ( 1 )

• 首先

在硬间隔的SVM中，我们加的约束是    yi(w⋅xi+b)≥1       y i ( w ⋅ x i + b ) ≥ 1 ，其中 1 表示的是margin的位置.

现在    yi(w⋅xi+b)≥1−ξi       y i ( w ⋅ x i + b ) ≥ 1 − ξ i 表示现在的函数距离现在只需要大于等于 1−ξi 1 − ξ i 就可以了。其中 ξi ξ i 表示 i i 样本偏离margin的距离。对于没有violation的样本， ξi=0 ξ i = 0 ，我们把 ξi ξ i 称为 松弛变量 。

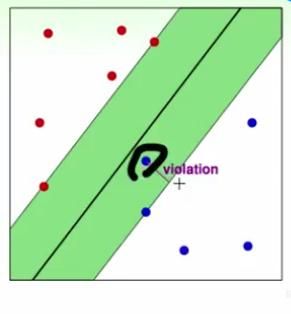
用下图来解释比较清楚：

图中有一个violate的点，它到 1 （也就是margin）的距离可以记为 ξi ξ i ，这个距离可以代表violate margin的程度。软间隔SVM为了容忍这个点，只需把约束条件中改为 1−ξi 1 − ξ i ，而不是限制在 1 处。

---

• 然后

ξi ξ i 代表violate margin的程度，我们希望 ξi ξ i 越小越好，因此在目标函数中，我们希望最小化 ∑Ni=1ξi ∑ i = 1 N ξ i

• 最后
  
  • 参数 C 代表了追求最大 margin 和 margin violation的一个tradeoff。
  • 当 C 设置比较大时，代表我追求违反margin的情形越少越好，边界瘦一点没关系（理解：dual 问题中， 0<a<c 0 < a < c ,当C为无穷大，等价于硬间隔）

---

4.2 软间隔SVM的对偶问题

4.2.1 软间隔SVM的对偶问题学习算法

(1) 选择惩罚参数 C>0 C > 0 , 构造对偶问题并求解关于 α α 的 最优解 α∗=(α∗1, ..., α∗N) α ∗ = ( α 1 ∗ ,   . . . ,   α N ∗ )

软间隔SVM的对偶问题,仅仅是在约束条件上，对拉格朗日系数 αi α i 添加了一个上限,也就是调和系数 C，soft- margin- dual 问题可以表示为：

minα    12∑Nj=1αiαjyiyj(xi⋅xj)−∑Ni=1αi m i n α         1 2 ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i

                                    
s.t.    ∑Ni=1αiyi=0 s . t .         ∑ i = 1 N α i y i = 0

            0≤αi≤C,i=1,2,...,N         (2)                         0 ≤ α i ≤ C , i = 1 , 2 , . . . , N                   ( 2 )

(2) 计算 w∗,b∗ w ∗ , b ∗ ，与硬间隔时的公式也完全一样.

其中， w∗ w ∗ 是输入 x x 的线性组合：

w∗=∑Ni=1 α∗iyi xi w ∗ = ∑ i = 1 N   α i ∗ y i   x i

算好 w∗ w ∗ 后，从 α∗=(α∗1, ..., α∗N) α ∗ = ( α 1 ∗ ,   . . . ,   α N ∗ ) 中挑选一个 α∗j,0<α∗j<C α j ∗ , 0 < α j ∗ < C ,并按下式求出 b∗ b ∗ .

b∗=yj−∑Ni=1α∗iyi(xi⋅xj) b ∗ = y j − ∑ i = 1 N α i ∗ y i ( x i ⋅ x j )

因此，b的解并不是唯一的，实际上计算时，可以取说有符合条件的样本点上的平均值。

---

注：

证明过程其实与前面基本相同。先把soft-margin经典问题转为关于拉格朗日函数的无约束问题，则对偶问题是先对拉格朗日函数 L(w,b,ξ,α,β) L ( w , b , ξ , α , β ) 的极大极小化问题。

这里的拉格朗日函数是：

L(w,b,ξ,α,β)=12||w||2+C∑Ni=1ξi+∑Ni=1αigi(x)−∑Ni=1βiξi L ( w , b , ξ , α , β ) = 1 2 | | w | | 2 + C ∑ i = 1 N ξ i + ∑ i = 1 N α i g i ( x ) − ∑ i = 1 N β i ξ i

                  =12||w||2+C∑Ni=1ξi+∑Ni=1αi(1−ξi−yi(wxi+b))−∑Ni=1βiξi    (3)                                     = 1 2 | | w | | 2 + C ∑ i = 1 N ξ i + ∑ i = 1 N α i ( 1 − ξ i − y i ( w x i + b ) ) − ∑ i = 1 N β i ξ i         ( 3 )

比较重要的KKT条件：

• 这里 L L 对 ξ ξ 求偏导并令其为0会得到： C−αi−βi=0 C − α i − β i = 0 ,这一结果代入(3)后将带有 ξ ξ 的项全部去除，因此，目标函数变为和硬间隔时的一样。
• w∗,b∗ w ∗ , b ∗ 的获取用到了互补松弛条件：
  
  • α∗i(yi(w∗⋅xi+b∗)−1+ξ∗i)=0 α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 + ξ i ∗ ) = 0
  • β∗iξ∗i=0(C−αi−βi) β i ∗ ξ i ∗ = 0 ( C − α i − β i )

---

4.3 软间隔SVM的支持向量

软间隔的支持向量 xi x i 存在四种类型的点：

• 在间隔边界上: 0<αi<C 0 < α i < C , 此时必有 ξi=0 ξ i = 0 (互补松弛条件 β∗iξ∗i=0 β i ∗ ξ i ∗ = 0 )
• 在margin和超平面之间: αi=C,0<ξi<1 α i = C , 0 < ξ i < 1
• 在超平面上: αi=C,0<ξi=1 α i = C , 0 < ξ i = 1
• 在超平面误分类一侧： αi=C,ξi>1 α i = C , ξ i > 1

理解： ξi ξ i 表示偏离边界的多少

---

4.4 实用的工具

• 对于线性的软间隔SVM：LIBLINER
• 非线性：LIBSVM