Andrew Ng机器学习笔记+Weka相关算法实现（三）神经网络和参数含义

神经网络是一种非常重要的机器学习模型，人们从生物学中大脑神经元连接方式得到启发，提出了神经网络的概念，它从信息处理角度对人脑神经元网络进行抽象， 建立某种简单模型，按不同的连接方式组成不同的网络。
最近几年深度学习大热,尤其是阿尔法围棋（AlphaGo）战胜李世乭后，神经网络和深度学习被推到了风口浪尖的。AlphaGo主要工作原理是“深度学习”。“深度学习”是指多层的人工神经网络和训练它的方法。一层神经网络会把大量矩阵数字作为输入，通过非线性激活方法取权重，再产生另一个数据集合作为输出。这就像生物神经大脑的工作机理一样，通过合适的矩阵数量，多层组织链接一起，形成神经网络“大脑”进行精准复杂的处理，就像人们识别物体标注图片一样。
人工神经网络模型主要考虑网络连接的拓扑结构、神经元的特征、学习规则等。目前，已有近40种神经网络模型，其中有反传网络、感知器、自组织映射、Hopfield网络、波耳兹曼机、适应谐振理论等。根据连接的拓扑结构，神经网络模型可以分为：
（1）前向网络 网络中各个神经元接受前一级的输入，并输出到下一级，网络中没有反馈，可以用一个有向无环路图表示。这种网络实现信号从输入空间到输出空间的变换，它的信息处理能力来自于简单非线性函数的多次复合。网络结构简单，易于实现。反传网络是一种典型的前向网络。

（2）反馈网络 网络内神经元间有反馈，可以用一个无向的完备图表示。这种神经网络的信息处理是状态的变换，可以用动力学系统理论处理。系统的稳定性与联想记忆功能有密切关系。Hopfield网络、波耳兹曼机均属于这种类型。
Ng的课程里神经网络讲的比较少，这次主要听了加州理工学院的公开课：机器学习与数据挖掘，地址是：
http://open.163.com/movie/2012/2/I/D/M8FH262HJ_M8FU27PID.html
我将总结老师讲解的神经网络概念、反向传播等知识进行总结，如有错误之处，请批评指正。

• 问题提出

简单的多层感知器不能够进行复杂的分类工作。

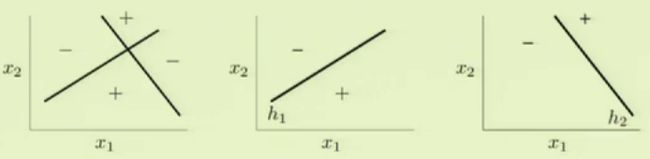
对于第一个图中的两类，简单线性感知器并不能正确的分类，但是我们可以构建第二第三两个基本感知器，将两个感知器进行某种方式的联结，合成一个更加强大的感知器。

第一个感知器因为有一个不变的输入1.5>1，因此必须X1，X2都是负的才能使得输出为负，这就实现了or运算，同理第二个感知器实现了AND运算。

我们把基本感知器进行组合，就可以得到复杂的感知器，理论上它可以模拟任何曲面。如图，输入X0，X1，X2，通过or、and感知器进行运算，可以得到复杂的输出f，这就是多层感知器的原理。图中是前馈网络，所谓前馈，就是输出只能向后传递，不能对之前的结果产生作用。图中一共有三层感知器，分别是输入层，隐含层和输出层，每一层后面的数字代表权重，也是我们要求的量。

如上图所示，通过使用16层感知器，我们可以得到一个非常接近圆的区域，这就形象的表示了为何理论上神经网络可以拟合任何复杂函数。理论上讲虽然越多的感知器可以带来更好地逼近效果，但是也会带来两个问题，那就是降低泛化能力和带来优化上的困难。

• 神经网络

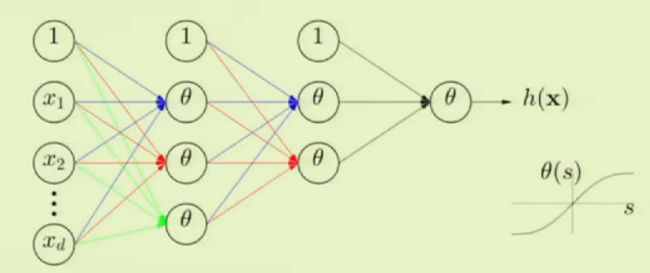
上图就是一个典型神经网络的结构，每一层都是非线性的，图中一共有三层。非线性是由感知器的激励函数产生的，比如常用的tanh函数：

从以上分析我们可以知道，我们求取的就是连接神经元之间的权重，首先我们对权重进行符号化表示：

输入之所以从0开始是因为每一层都会有一项常数，即X0。
不难看出，右边层的输入其实就是前一层的输出。那么我们可以得到表达式：

其中S就是信号，对于输入的变量，每一层经过计算产生输出，层层计算直到输出层。那么如何构建出这个神经网络呢？关键就在于W的计算，我们需要计算出所有的权重，并保证权重是最优的。这是一个计算量非常大的工作，必须引入高效的计算方式才能解决。

• 反向传播算法

我们可以利用随机梯度下降求取最佳的权重，但是仍然不能避免巨大的计算量，所以我们应该分析层与层之间的关系，利用这些关系简化计算。根据前两篇博客的内容，我们首先表达出误差项：

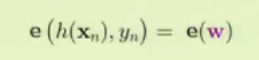
接下俩就是求取梯度：

对于一个神经元连接来说：

我们可以发现，W权重其实是X和S之间的桥梁，也就是X通过权重作用于信号S上，不受其他变量的影响。那么利用求导的链式法则：

我们可以将这种关系进行分解，不难看出，S和W之间的求导关系其实就是X，接下来我们要求的就是第二项，我们暂时令它为δ。
因为最后一层结果就是输出，因此先分析最后一层应该是最简单的，那么对于最后一层，我们可以得到：

其中：

又有如下公式：

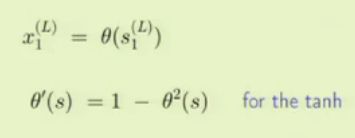
观察整个层与层之间的关系，我们不难发现，每一层的输出作为下一层的输入，这种关系层层传递，那么我们可以表示出相邻两层之间的关系：

利用求导的链式法则：

因此我们可以得到化简后的结果：

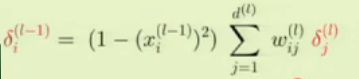
这样我们就得到了δ层与层之间的递推关系，也就是说，我们知道最后一层的δ，就可以倒着推出所有的δ，这就避免了每次一个一个计算W，可以迭代进行整个过程，因此BP算法的整个过程可以表述如下：

这里需要注意的是，初始化权重W不能全部为0，因为这样相当于层与层之间没有任何关联，每次更新迭代并不会有任何效果。这就像你站在山顶，如果没有外部力量推一把，你永远不会滚下山，到达最低的地方。因此，初始化权重应该随机赋值才能保证效果。事实上随机思想还可以避免陷入到非常明显的局部最优解，这对算法来说非常有效。

• Weka中实现神经网络

首先要知道的是，每次学习之前，输入的数据被自动分成training set、validation set 及test set 三部分，training set是训练样本数据，validation set是验证样本数据，test set是测试样本数据，这样这三个数据集是没有重叠的。在训练时，用training训练，每训练一次，系统自动会将validation set中的样本数据输入神经网络进行验证，在validation set输入后会得出一个误差（不是网络的训练误差，而是验证样本数据输入后得到的输出误差，可能是均方误差），而此前对validation set会设置一个步数，比如默认是6echo，则系统判断这个误差是否在连续6次检验后不下降，如果不下降或者甚至上升，说明training set训练的误差已经不再减小，没有更好的效果了，这时再训练就没必要了，就停止训练，不然可能陷入过学习。
Weka中提供了多层感知器，MultilayerPerceptron，它使用的激励函数是sigmod函数，看一下它主要的可用参数：

下面逐个解释每个参数的作用：
① -L 学习速率
学习速率，也就是梯度下降的速度。
学习速率的选取很重要 ，大了可能导致系统不稳定，小了会导致训练周期过长、收敛慢，达不到要求的误差。一般倾向于选取较小的学习速率以保持系统稳定，通过观察误差下降曲线来判断。下降较快说明学习率比较合适，若有较大振荡则说明学习率偏大。同时，由于网络规模大小的不同，学习率选择应当针对其进行调整。采用变学习速率的方案，令学习速率随学习进展而逐步减少，可收到良好的效果。
② -M 动量
BP神经网络在批处理训练时会陷入局部最小，也就是说误差能基本不变化其返回的信号对权值调整很小但是总误差能又大于训练结果设定的总误差能条件。这个时候加入一个动量因子有助于其反馈的误差信号使神经元的权值重新振荡起来。从权重更新的公式上看：

最后一项的α就是动量的系数。引入动量可以加快神经网络收敛。
③ -N 迭代次数
由于神经网络计算并不能保证在各种参数配置下迭代结果收敛，当迭代结果不收敛时，允许最大的迭代次数。
④ -V
Validation set的百分比，训练将持续直到其观测到在validation set上的误差已经一直在变差或者不变，或者训练的时间已经到了 。
如果validation set设置的是0那么网络将一直训练直到达到迭代的次数
⑤ -E
用于终止validation testing。这个值用于决定在训练终止前在一行内的validation set error可以变差（或者不变）多少次 。
⑥ -H 每层的神经元数
通用符 ‘a’ = (attribs + classes) / 2, ‘i’ = attribs, ‘o’ = classes , ‘t’ = attribs + classes
⑦-R 重置
将允许网络用一个更低的学习速率复位。如果网络偏离了方向其将会自动的用更低的学习速率复位并且重新训练。若没有加这个参数，偏离方向后训练将返回失败信息。
⑧ -D延迟
这个参数可以导致学习的速率的降低。其将初始的学习速率除以迭代次数（epoch number）去决定当前的学习速率。这对于停止神经网络背离目标输出有帮助，也提高了general performance。

其他参数比较简单，涉及到的都是数据挖掘基本知识，不再赘述。
下面是代码示例：

class NeuralNetworkModel  {
    public NeuralNetworkModel(Instances data) throws Exception{
        String[] options = {"-L",0.1,"-M",0.1,"-N",1000,"-H",4}
        MultilayerPerceptron model = new MultilayerPerceptron();
        modeloptions = options;
        model.setOptions(options);
        model.buildClassifier(data);
    }
}

如上创建的是一个具有一个隐含层的网络，如果想创建两个隐含层的网络，每一层都指定若干个神经元，参数应该写成：
setHiddenLayers(“4,5”) 或者 “… -H 4,5”
代表两个隐含层，第一层4个神经元，第二层5个神经元。

需要注意的是，神经网络一个非常难以确定的是隐含层层数和每层神经元数的选择，一般都按照经验进行选取，对于线性问题一般可以采用感知器或自适应网络来解决，而不采用非线性网络，因为单层不能发挥出非线性激活函数的特长。对于非线性问题，一般采用两层或两层以上的隐含层，但是误差精度的提高实际上也可以通过增加隐含层中的神经元数目获得，其训练效果也比增加层数更容易观察和调整，所以一般情况下，应优先考虑增加隐含层中的神经元数。对于数量，一般按照（属性数目+类别数目）/2来选取，并留一点余量。
对于每个参数影响有多大，可以看下面这张图：