手推SVM（三）-软间隔和损失函数的推导

1. 软间隔的提出
2. 对偶问题及其化简
3. 参数的求解
4. 参数的调优

1.软间隔的提出

上一篇文章（手推SVM（二）-核方法 ）我们用核方法来解决线性不可分问题，但如果即使映射到高维空间中，仍然有部分点不能完美的区分开呢？

如图，无论核函数怎么选取，都不能完美区分开数据，即使能完美的区分开数据，也会很容易导致过拟合的发生，这时候我们该怎么办呢？

既然人在做某事的时候，能允许犯一点小错，那模型为什么就不能允许犯一点小错呢？这就是软间隔的想法，既然确实无法区分开，那我就允许部分点分类错误就OK了，因为那部分点也有可能是离群点或噪声数据。

换成公式就是：
pocket表示允许部分点的预测标签与真实标签不一致，但只要这个不一致的数据数量最小就好了。

把两者结合起来，就是：

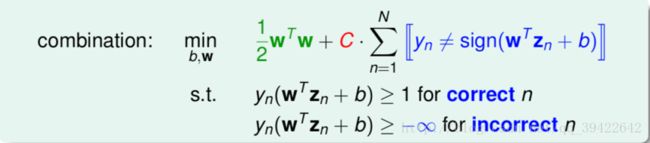
对于部分样本允许它的值大于负无穷，也就意味着允许它分类错误，参数C的作用就是为限制分错的样本数量，调整C可以让模型是更注重margin还是更注重分错的数量，使模型的准确率保持在一定范围内。

把两个条件合成一个条件，表示如果它分类正确的话，就让我们更注重margin。

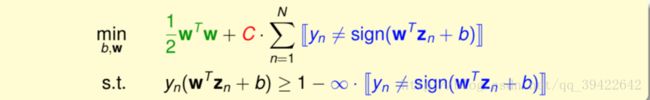
但是，发现这个条件约束不是一个线性函数，如果不是线性函数，那我们之前所推导的对偶问题，核函数就都不能使用了，那该怎么办才好呢？

那我们上面是看分类错误的个数，那既然分类错误了，我们能不能看一下错的有多离谱呢？就像我们和你偶像之间的距离，你应该想知道你和他到底差了多少个级别，哪里离得比较远，你就知道自己哪里不足了，然后慢慢的学习，私底下慢慢的改进，模型也一样呀，那我们可以不记录到底错了多少个，我们看一下分类错误的样本还差多少能被分类正确，因此定义了 ξn ,它表示分类错误的时候，还需要多少距离，才能被分类正确。

用图形表示 就是希望如下违规点的violation的长度越小越好，最好小于等于0.其中C在其中的作用就是控制间隔的大小和违规的样本数量。C越大，就代表我们希望违规的样本越少越好，哪怕这个margin（街宽）变小也无所谓；C越小，就代表允许有很多违规的样本，但希望我们的margin大一点比较好。

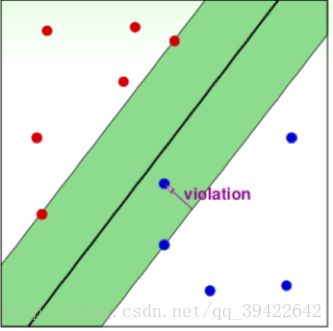
其实这样的计算误差的方法就是SVM中的损失函数，我们通过一个图像识别的例子看一下它具体是怎么做的？
详细例子：
hinge loss/线性SVM的损失函数

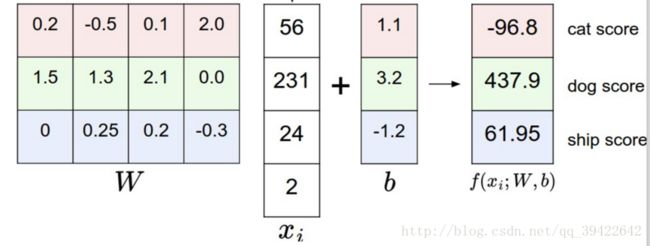
假设上面那张猫的图片数据为 xi ,其他还有狗和船的，在W下有一个得分向量

f(x,W)=[13,−7,11]

,分别代表猫，船，狗的得分，但正确答案是猫，也就是第一个,hinge loss希望正确答案与错误答案之间的得分差距在某一阀值范围内，假设为10，就可以得到

Li=max(0,−7−13+10)+max(0,11−13+10)=0+7=7

因为猫和狗的得分之间的差距不满足阀值，就会增加一个损失，而猫和船之间的差距符合阀值10，所以船这个分类就不会带来任何损失。
用公式表示:

Li=∑max(0,错误的得分−正确的得分+阀值)

2.对偶问题及其化简

由上图可知，我们最后的优化条件变成了两个，同样使用拉格朗日乘子法进行求解有：

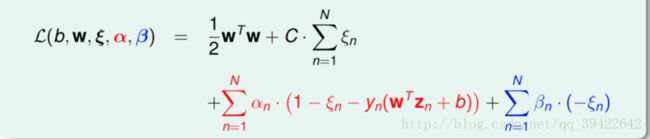
于是得到这样的优化问题：

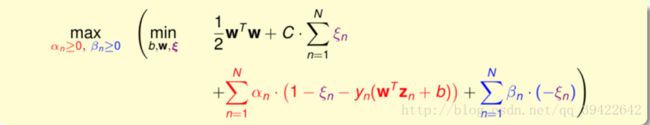
按照我们的老套路，先化简：

∂L∂ξn=0=C−αn−βn

可得： βn=C−αn,因为βn>0,所以:0<αn<C ,把 β 代入上式有：

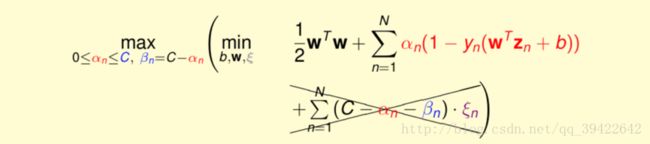
同样对其他参数化简，最后仍然可以得到我们在（手推SVM（一）-数学推导）中得到的类似结果，只是他们的约束条件有些许变化。即 αn 的上限不再是无穷远，而是C了。

3.参数的求解

在hard-margin中，我们知道可以直接通过一个条件就可以求出对应的b了，但是对于soft-margin呢？
因为对应的KKT条件又有了新的变化，所以对应的求解方法又有了新的变化，因为加了 ξn ,所以求b时的改成了这个样子，其中因为 βn=C−αn ,同时负号没什么影响，所以对soft-margin的条件就可以改成如下右图这个样子了。

使用第一个条件可以得到:

b=ys−ysξs−wTzs

但其中有 ξs 是我们不知道的，所以通过第二个条件，令 ξn=0 ,可得到

0<αs<C

如此就可以得到：

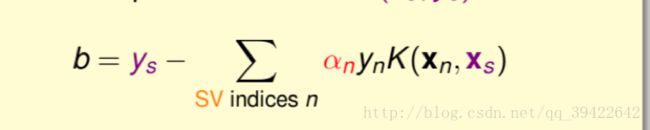
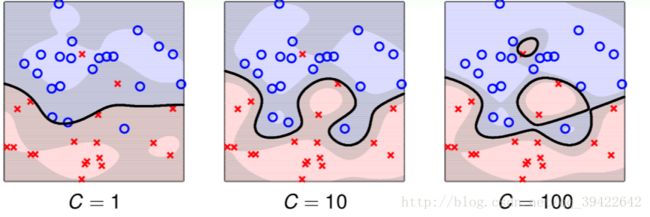
下图是不同的C取值，形成的分类边界，可以发现如果C没有好好选的话，也还是很容易过拟合的。同时C越大，它的宽度就会越小，而犯错的点也会越少。

再分析一下其他一些参数的实际意义：

• 如果 0<αn<C，则ξn=0 ,我们刚才就是用这个条件算出的b，由第一条式子可以得到：
  1=yn(wTzn+b)
  ,也就是y乘上分数刚好等于1的点，刚好在边界上（图中画方框的点）。
• αn=0 ,那第二式的 ξn=0 ,代表了那些没有范围条件上的点（图中正常的圈圈和叉叉）。
• αn=C ,那由第一式就有：
  ξn=1−yn(wTzn+b)
  刚好记录了违反边界的点的违反程度，违反了多少（图中三角形的点）。

4.参数的调优

大家最常见的调优方案就是交叉验证了，在这里不说了，说点别的。
Leave-One_Out-CV error
其实就是把100份样本切成100份，留一个作为验证，其余作为训练。而在SVM中可以得到：

留一交叉验证的误差≤支持向量样本数

也就是说，假如你有10000个样本，有100个支持向量，那么你的leave one out 的交叉验证误差小于100.

那这个该怎么证明呢？
假如最后一个点 （xN,yN） 是一个非支持向量，即 αN=0 ,你把其余的9999个点送进去的时候，这一组 (α1,α2,…,αN−1) ，还是最佳解。为什么呢？因为如果这一组不是最佳解，就意味着有一组更好的 ，那你把这个点加回去，又有一组更好的，那就矛盾了，因为拿出来的那个点 （xN,yN） 不是支持向量，在分类的时候对误差不会做出什么贡献。而即使有误差，每个样本也应该是小于等于1的，所以有了这个结论。

参考
机器学习技法