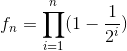2020牛客多校（第六场）
B-Binary Vector
- 看样例可得
,
- 答案
,只需要求一次2的逆元就够了
-
#include
-
using
namespace
std;
-
typedef
long
long LL;
-
const
int mod =
1e9+
7;
-
const
int N =
2e7+
10;
-
LL POW(LL x,LL y)
-
{
-
LL ans=
1;
-
while(y){
-
if(y&
1)ans=ans*x%mod;
-
x=x*x%mod;
-
y>>=
1;
-
}
-
return ans;
-
}
-
LL inv(LL x){
-
return POW(x,mod
-2);
-
}
-
LL a[N];
-
void init(){
//预处理答案
-
LL inv2=inv(
2);
-
LL ans=
0,res=
1,sum=inv2;
-
for(
int i=
1;i
-
res=res*(
1-sum+mod)%mod;
//更新f
-
sum=sum*inv2%mod;
//更新分母
-
ans^=res;
//更新g
-
a[i]=ans;
-
}
-
}
-
int main()
-
{
-
init();
-
int t;
cin>>t;
-
while(t--){
-
int x;
cin>>x;
-
cout<
endl;
-
}
-
system(
"pause");
-
return
0;
-
}
C-Combination of Physics and Maths
- 一列一列的去找，因为两列合并时
,即合并之后的值处于两者之间不超过较大值，那么就没有合并的意义了，一列一列的更新最大值。
- 因为分母是选取的子矩阵的最后一行，因此可以扩大分子，即从第一行开始加到子矩阵末尾。
-
#include
-
using
namespace
std;
-
int a[
205][
205],b[
205][
205];
-
int main(){
-
int t;
-
scanf(
"%d",&t);
-
for(
int i=
0;i
-
int n,m;
double mx=
-1;
-
scanf(
"%d%d",&n,&m);
-
for(
int i=
1;i<=n;i++){
-
for(
int j=
1;j<=m;j++){
-
scanf(
"%d",&a[i][j]);
-
b[i][j]=b[i
-1][j]+a[i][j];
//前缀和
-
mx=max(mx,b[i][j]*
1.0/a[i][j]);
-
}
-
}
printf(
"%.8lf\n",mx);
-
}
-
return
0;
-
}
E-Easy Construction
- 构造题。问1-n的排列是否能组成一个这样的序列，使得他同时存在长度为1-n的连续子序列，他们的和都满足sum%n=k%n
- 首先长度为n的子序列只有一个（它本身），那么sum=n*(n+1)/2,如果k不满足sum%n==k%n的话，直接输出-1
- n为奇数时，sum%n=0,那么就这么构造n,1,n-1,2,n-2...n/2,n/2+1
- n为偶数时，sum%n=n/2,那么就这么构造n,n/2,1,n-1,2,n-2...n/2-1,n/2+1
-
#include
-
using
namespace
std;
-
#define LL long long
-
int main(){
-
int n,k;
-
cin>>n>>k;
-
int sum=n*(n+
1)/
2;
-
if(sum%n!=k%n)
cout<<
-1<<
endl;
-
else
if(n&
1){
-
cout<
-
for(
int i=
1;i<=n/
2;i++)
cout<<
" "<
" "<
-
cout<<
endl;
-
}
else{
-
cout<
" "<2;
-
for(
int i=
1;i
2;i++)
cout<<
" "<" "<
-
cout<<
endl;
-
}
-
system(
"pause");
-
return
0;
-
}
G-Grid Coloring
- 构造题。拿k种不同颜色 火柴拜访成n*n个正方形，必须满足：
- 每种颜色的火柴花的数量相同
- 一个正方形环上不能都是相同颜色的火柴
- 每行每列火柴不能全部相同
- n=1和k=1的情况肯定摆不出
- 可以按照从左到右依次1 2 3 4 5...摆放
- 如果n是k的倍数的话，如果还是从左到右扫描的话，那么左上角的正方形四条边都会是同样的颜色，不满足条件，所以另起一行是++tmp
- 如果n不是k的倍数的话，那么不影响
-
#include
-
using
namespace
std;
-
#define sc(a) scanf("%d",&a)
-
int n,k;
-
void color(){
-
int tmp=
0;
-
if(n%k){
-
for(
int i=
1;i<=(n+
1)*
2;i++){
-
for(
int j=
1;j<=n;j++){
-
tmp=tmp%k+
1;
-
cout<
" ";
-
}
-
cout<<
endl;
-
}
-
}
else{
-
for(
int i=
1;i<=(n+
1)*
2;i++){
-
for(
int j=
1;j<=n;j++){
-
tmp=tmp%k+
1;
-
cout<
" ";
-
}tmp=tmp%k+
1;
-
cout<<
endl;
-
}
-
}
-
}
-
int main(){
-
int t;sc(t);
-
for(
int i=
0;i
-
sc(n);sc(k);
-
if(n==
1||k==
1||
2*n*(n+
1)%k)
puts(
"-1");
-
else color();
-
}
-
return
0;
-
}