机器学习笔记——logistics的python实现
机器学习笔记——logistics的python实现
- 参考书籍
- 方法优缺点
- sigmod函数
- 梯度上升算法
- python实现
- 样本数据生成
- logistics程序介绍
- 数据读取
- sigmod函数
- 梯度上升迭代求最佳系数
- 小结
对于logistics回归,能利用回归的方法实现对目标数据的分类(0或1,这取决于sigmod函数的特性),是一种非常有用的分类方法,下面对其实现过程进行介绍。
参考书籍
参考书籍:人民邮电出版社——图灵程序设计丛书《机器学习实战》
方法优缺点
优点:计算代价不高,易于理解和实现
缺点:容易欠拟合,分类精度不高
适用于数值型和标称型数据
sigmod函数
要用连续回归的方法实现二值型数据输出,就要借助这个sigmod函数,同时肯定不能随意的使用一个函数来进行操作,这个函数要满足一个条件,参数输入后输出的结果为0或者1,这里使用的是如下的函数:
| 1 1 + e − z \frac{1}{1+e^{-z}} 1+e−z1 |
|---|
可以观察一下这个函数,其图形如下:

可以看到在x=0时,函数值为0.5;在 x → + ∞ x\to+\infty x→+∞时,取值接近1,在 x → − ∞ x\to-\infty x→−∞时,取值接近0。那么通过将特征值与系数相乘转换为z,则可将样本映射在此连续函数上,映射至区间[0,1],若 g ( z ) > 0.5 g(z)>0.5 g(z)>0.5,则分类为1;若 g ( z ) < 0.5 g(z)<0.5 g(z)<0.5,则分类为0。
其中特征映射至连续函数的过程如下:
| z = w 0 x 0 + w 1 x 1 + . . . + w n x n z=w_0x_0+w_1x_1+...+w_nx_n z=w0x0+w1x1+...+wnxn |
|---|
那么下一步要考虑的问题就是如何确定最佳系数 w i w_i wi,如何在最大的概率下将样本进行正确的分类,这就要用到梯度上升算法了,有兴趣可以搜索一下论坛中的文章,论坛中有对梯度上升算法的证明及通俗理解的讲解,这里不做过多的赘述。
梯度上升算法
梯度上升算法的公式如下:
| w : = w + ▽ w g ( w x ) w :=w+\bigtriangledown_w g(wx) w:=w+▽wg(wx) |
|---|
如何对样本进行梯度计算呢?这就要设计到上述提到的数学证明了,证明结果中,可将上述的参数定义公式转化为如下形式:
| w : = w + α ∑ i = 1 n ( y i − g w ( x i ) ) ⋅ x j i w := w + \alpha \sum_{i=1}^{n} (y^i-g_w(x^i))·x_j^i w:=w+α∑i=1n(yi−gw(xi))⋅xji |
|---|
即如下:
| w : = w + α ∑ i = 1 n w := w + \alpha \sum_{i=1}^{n} w:=w+α∑i=1n(样本实际的分类 - 模型计算的分类)·样本特征值 |
|---|
其中,样本实际的分类 - 模型计算的分类即根据模型计算的误差,由误差来重新定义参数 w i w_i wi,再次计算误差;通过不断的迭代,最后达到要求的精度(精度达到要求或者达到一定的迭代次数)。 α \alpha α为迭代的步长,大致可以理解为对参数修正的幅度。
python实现
解决了参数的迭代问题,那么就剩下代码的实现了,代码的实现过程如下:
样本数据生成
由于没有找到书中及网上常用的样本数据,就自己生成了一组随机数据,特征 x 1 x_1 x1和 x 2 x_2 x2为[5,20]的随机浮点数,根据 y = x y=x y=x此直线分类数据类别,即 x 1 < x 2 x_1<x_2 x1<x2时,归类为类别1; x 1 > x 2 x_1>x_2 x1>x2时,归类为类别0。
同时添加了一列为 x 0 x_0 x0,为什么添加此列呢?我说下个人的理解:在我们的实际应用中,我们要画条线对样本进行分类,那么假如不加 x 0 x_0 x0,两个参数 w i ( i = 1 , 2 ) w_i(i=1,2) wi(i=1,2)生成的直线为 w 1 x 1 + w 2 x 2 w_1x_1+w_2x_2 w1x1+w2x2,显然这是不合理的,因为虽然我们这里生成的样本是按照 y = x y=x y=x作为界限进行分类的,但是不是所有情况都没有截距项的,且若分类直线没有截距项,就是截距为0的情况。
但是实际分类样本中并没有 x 0 x_0 x0这一项,如何确定呢?其实只要随意定一个就行,原因如下:首先分类的重点其实在 x 1 x_1 x1和 x 2 x_2 x2,同样无论将 x 0 x_0 x0设置为什么,在不断迭代的过程中将会不断的修正系数。这里添加时将 x 0 x_0 x0设置为1.0,试想一下,假如正确的 x 0 x_0 x0系数为1,那设置成2.0时,系数就为0.5。
生成样本的代码如下:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
data = np.zeros((100,4))
x1 = []
y1 = []
x2 = []
y2 = []
# 随机数生成样本
data[:,0] = np.random.uniform(1,1,100)
data[:,1] = np.random.uniform(5,20,100)
data[:,2] = np.random.uniform(5,20,100)
# 按照y=x为界限将样本分类
for ii in range(data.shape[0]):
if data[ii,2] >= data[ii,1]:
x1.append(data[ii,1])
y1.append(data[ii,2])
data[ii,3] = 1
else:
x2.append(data[ii,1])
y2.append(data[ii,2])
data[ii,3] = 0
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x1,y1,marker='*')
ax.scatter(x2,y2)
# 画出y=x分类界限
x = [4,21]
y = x
ax.plot(x,y)
# 可视化参数设置
plt.xlim(3,22)
plt.ylim(3,22)
plt.title('样本生成')
plt.text(20,20,'分类直线:y=x')
plt.show()
#data = pd.DataFrame(data,columns=['x0','x1','y1','classlabel'])
#data.to_excel('./program/data/machine_learning/logistic_eg.xlsx',index=False)
样本如下:
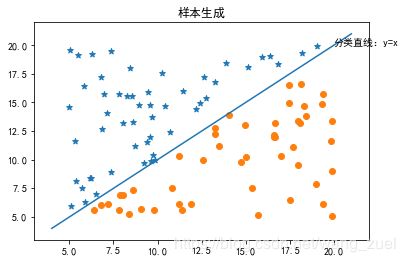
得到的样本数据,需要保存至如下的格式,方便统一用于logistics的处理,将样本的特征放在前面,将分类结果放在最后一列,格式如下:
logistics程序介绍
数据读取
由上述的样本格式,这里选择用pandas方式读取数据,个人习惯,数据读取后将样本特征 x i ( i = 0 , 1 , 2 ) x_i(i=0,1,2) xi(i=0,1,2)和样本分类分割出来分别返回。
def load_data(filepath):
"""
数据读取
"""
data = pd.read_excel(filepath)
feature_data = data.iloc[:,:-1] # 将样本特征数据分割出来
data_label = data.iloc[:,-1] # 将样本分类结果分割出来
return feature_data,data_label
sigmod函数
这个就比较简单了,不多说,这里处理用的是numpy(因为涉及到矩阵的相乘):
def sigmod(parameter):
"""
sigmod函数
"""
return 1/(1+np.exp(-parameter))
梯度上升迭代求最佳系数
def grad_Acent_1(featureData,classLabel,cycles=500):
"""
梯度上升算法1:每次要计算整个矩阵,样本量大、特征多时计算复杂程度较高
此处默认迭代500次
"""
dataMat = np.mat(featureData) # 转化为矩阵形式
labelMat = np.mat(classLabel).transpose() # 转化为矩阵形式
m,n = dataMat.shape
alpha = 0.01
weights = np.ones((n,1))
for ii in range(cycles):
test = sigmod(dataMat*weights)
test_error = labelMat - test # 根据计算的误差来调整weights
weights = weights + alpha*dataMat.transpose()*test_error # 这里不清楚的可以参考一下矩阵相乘的规则,weights为n*1的矩阵,要迭代,就应该为(n*m)*(m*1)=n*1
return weights
得到结果如下:
>>> data_path = './program/data/machine_learning/logistic_eg.xlsx'
>>> feature_data,data_label = load_data(data_path)
>>> weights = grad_Acent_1(feature_data,data_label)
# 结果:
[[ 0.61014592]
[-13.3813473 ]
[ 13.38748865]]
def plot_result(featuredata,datalabel,weights):
"""
分类结果展示:此函数只适用于二维数据
"""
featuredata = np.array(featuredata)
datalabel = np.array(datalabel)
# logistics分类
x1 = []
y1 = []
x2 = []
y2 = []
for ii in range(featuredata.shape[0]):
if datalabel[ii] == 1:
x1.append(featuredata[ii,1])
y1.append(featuredata[ii,2])
else:
x2.append(featuredata[ii,1])
y2.append(featuredata[ii,2])
# 可视化
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x1,y1,marker='*')
ax.scatter(x2,y2)
# 画出logistics分类界限
x_fit = np.arange(4,21,0.1)
y_fit = -(weights[0,0] + weights[1,0]*x_fit)/weights[2,0]
ax.plot(x_fit,y_fit,color='r')
# 可视化参数设置
plt.title('logistics分类结果')
plt.text(x_fit[0],y_fit[0],'分类界限:y=%.4fx+%.2f'%(-weights[1,0]/weights[2,0],-weights[0,0]/weights[2,0]))
#plt.savefig('./program/data/machine_learning/logistic_eg_fit.png')
plt.show()
在梯度上升算法中,可以设定迭代的次数,也可以设置循环结束的条件为系数达到一定精度,这里设置了默认迭代500次,可以看到结果并不是特别完美,我们在样本生成中使用的分类界限其实为 y = x y=x y=x,这里算出来的有些差别,但是分类的效果还是可以的,要是训练的样本更多,效果应该会更好。
小结
至此,已经使用python实现了logistics回归,但是在梯度上升算法中,使用时每次都要计算整个样本矩阵相乘,需要消耗大量的算力,所以在下一篇文章机器学习笔记——logistics梯度上升算法的改进中将介绍使用较为简洁的方式实现梯度上升算法。

