关于SVM的个人理解（结合吴恩达老师Coursera课程）

0.前言

自学机器学习有一段时间了，一开始看到吴恩达老师《机器学习》课程SVM部分不是很理解就先搁置下来，现在毕设拿CNN做的差不多了，看到很多研究借助SVN与CNN相结合的方式获得了更好的效果，所以折腾回来想把这一部分解决掉。

一开始看了网上很多帖子都是基于二维空间点到直线距离分析的，弄得我云里雾里，后来仔细想想列举原因如下：

(1)公式术语过多，一篇文章一个符号习惯，看着晕

(2)叙述比较偏理论，没有和工程应用有机结合起来。

要知道在框架语言（tensorflow甚至MATLAB）里面对于优化问题往往直接一个优化器搞定，深入搞懂每个优化器背后的原理费时费力，没俩礼拜你就忘了。相比之下我认为直接站在优化器想要什么效果的角度去思考更有利于实际编程。

于是温故知新，自己又回去把《机器学习》的SVM章节好好看了一遍，结合我自己在工程上的实践经验也有了一些新的理解。

1.SVM的目的是什么？

为方便起见这里假设一个只有2个特征（x1和x2）和2个类别的分类任务，如下图：

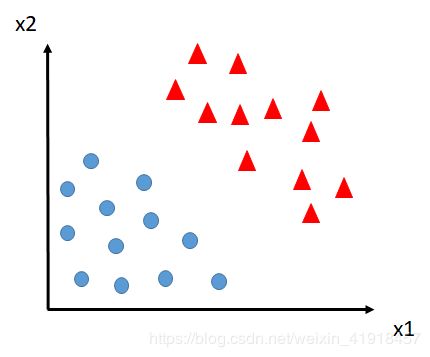
现在我们想找到一条线把这两个类别分开，下图中提供了几条直线让你选择，你肯定想选择绿色那条，因为看着最舒服、最标准。

没错，SVM设计的目的就在于此：光正确分类还不够，你还得分的标准。

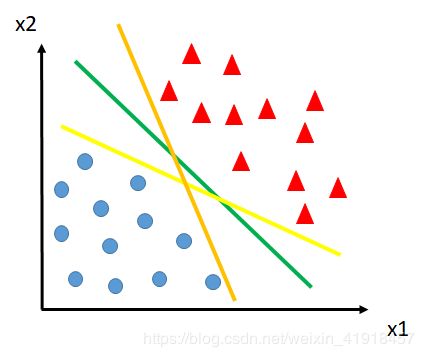
现在问题来了，怎么找到这条“完美边界”？接下来就不得不引入支持向量的概念了。

我们单拎出来看绿线，假设它就是最完美的分界线，那我们认为在分类任务中，这条线就有一个重要性质：两侧所有离自己最近的点，距离最大。（PS：如果你问为什么这样规定，不妨找上一张图里其他两条线拿来试试，看它们两侧最近的点，距离有绿线大吗）

下图中假设了三个这样的样本点（也至少3点，2点无法确定唯一分界），分别用虚线标出来了。仔细想想 ，去掉其他样本点这条直线照样存在，但去掉三点中的任何一点绿线就不稳了，所以是这三个点支持着绿线的存在，那这三个样本点就叫支持向量

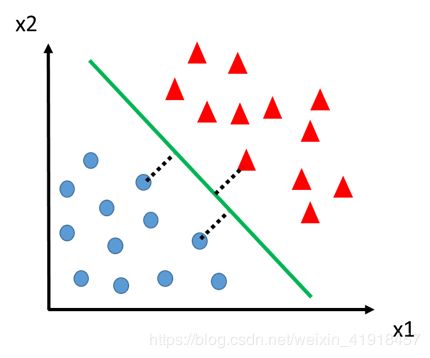
当然，在上面这张图里只有x1和x2两个特征，支持向量的维度也只有2，在特征丰富的训练任务里（比如每个样本点有100个特征），分类边界就从直线推广为超平面，但原理是一样的。

我们总结一下：训练过程中，SVM的优化器有两个任务：
（1）把类先分对了
（2）找到支持向量

下面看看优化器是怎么同时干这两件事的。

2、SVM如何实现

在逻辑回归中，我们已经引入交叉熵(cross entropy)函数作为损失函数（cost function），优化器需要优化的函数是：

其中 交叉熵损失 作为优化主体，承担着把loss降到最低的使命，而正则项只是打辅助，防止优化器过拟合

而在SVM中，我们将cost function变为合页损失（hinge loss），优化器目标函数调整如下：

此时合页损失仍作为优化主体，优化器在该部分完成第一个任务——把loss降到最低以正确分类；
而在正则项部分，优化器需要完成第二个任务：通过优化该项来找到支持向量

如何做到这一点？

我们梳理一下视频中的内容：


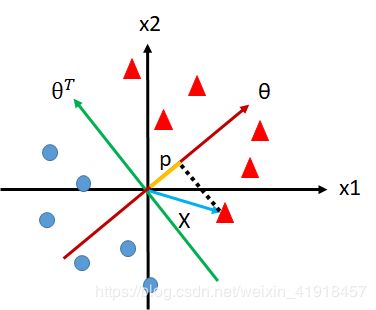
从上图我们可以看出，投影长度p实际代表了任意向量X（包括支持向量）到最优分界面θT的距离，这也是很多帖子的直接切入点——点到直线距离。

那我们回到刚才的问题发现，要想找到支持向量，只要在分类正确的前提下，让p尽可能的大不就好了？

而假设此时已经正确分类某个样本，那么θTX就可以暂时视为一个稳定的数值，对于p•||θ||来说，想要让p变大，那就要让 ||θ|| 变小。如何做到？

我们注意到正则项部分可化简为：

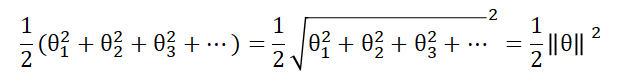
而优化器在最小化合页损失后，觉得loss值总体还不够小，一瞅还剩个正则项不大不小搁哪儿摆着，所以接下来优化器为了达到更低的损失值，会选择将 ||θ|| 最小化

于是，在 ||θ|| 最小化的同时，若想保持分类结果θTX稳定，p必将趋向于最大化，而p又是样本点X到分类边界的距离，当这个距离已经增大到某个极限值的时候，恭喜你，找到支持向量了。

3.进一步思考：如何定义分类稳定？

大家可能注意到，上文中我没有把θTX理解成一个固定值，而是反复用强调稳定分类这一概念，那么如何做到稳定？就是要满足一定约束条件。

我们看合页损失的函数曲线，和交叉熵类似，也分为两个部分。但不同的是，这里严格规定θTX≥1时分类结果才真正为正类，反之θTX≤-1才为负类，体现在函数值上就是对应区间loss=0

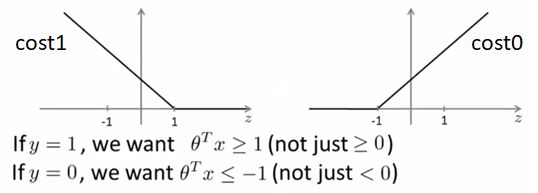
我们刚才说的稳定分类，就是指图中两式带入p和||θ||后，满足：

那你可能会问，为什么（图中也指出了）必须以1和-1为分界线，而不是0？

关于这点我个人的理解是，以p•||θ||≥0为例，由于||θ||本身恒为正，那么任意非负p即可轻松达到p•||θ||≥0，这样的后果是随便过来一个p（可能很小），优化器一看满足条件就不再继续优化了；而采用1作为分界线时，由于优化器可这劲儿的降低||θ||，要想使p•||θ||≥1，那么p就要可劲儿增大，直到找到支持向量（||θ||不再减小）为止。

一句话说就是，p•||θ||≥1比p•||θ||≥0更具有约束力，也因为多出来的这个1，给了优化器继续寻找最优边界的空间。

对于p•||θ||≤-1也是如此。

4.核函数：解决非线性不可分问题

刚才我们的所有讨论都是基于线性可分问题的，说白了，用一条线就能把样本分开，那如果长这样怎么办？

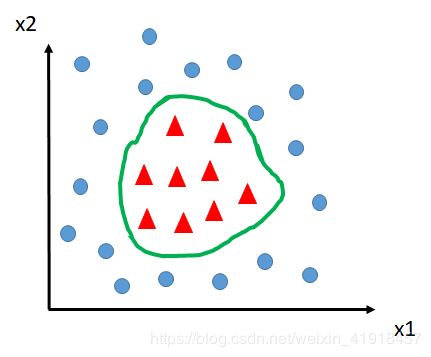
此时出现非线性不可分问题。 你说我们用一个圈给它圈出来，那么问题来了（吴恩达老师也指出这一点），圆圈的表达式可是非线性的，没准您画的圈转化成表达式是这样的：

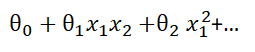
而我们都知道普通的矩阵运算是不支持这种非线性计算的，怎么办？

有人说了，那把非线性项x1x2这种转化成线性不就行了吗？

思路没错，但在SVM里我们不再直接对原始特征x转换，而是引入核函数 f 作为新的特征，这意味着我们要抛弃原来的特征。

引入核函数 f 后，样本边界表达式变为：

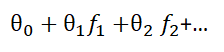
此时，非线性问题转化为线性问题。

我们刚刚提到抛弃原来的特征，那就意味着 f1不等于x1x2，f2也不等于x2的平方，所以现在需要一种新的方式来定义新特征。

核函数起到了这一层作用。在吴恩达老师的视频中采用了相似度(similarity)作为新特征，并使用高斯核函数来衡量这一标准：

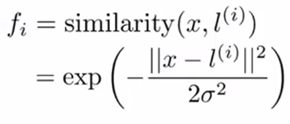
其中 l 为任意样本点向量，x为当前样本点向量，各下属一定数目的特征。

PS：拿人脸特征举个不太恰当的栗子：

此时，再把核函数代入到优化器目标函数中，得到：

于是，我们就将非线性不可分问题彻彻底底转化成了一个线性分类问题。

当然，对于原来没有使用核函数的情况，我们也习惯将之称为 “线性核函数”

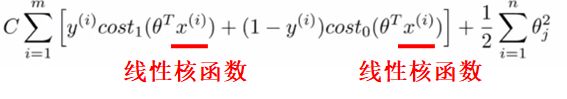
5. 和神经网络的联系

在神经网络中，如果采用交叉熵作为cost function ，那么该函数的输入将是激活函数（相当于假设函数）的预测输出，激活函数除了sigmoid函数外，还可选择relu、tanh、elu、relu6、leaky-relu等等：

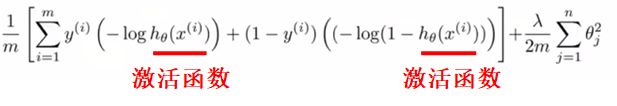
而SVM中，核函数起到了类似激活函数的作用，除高斯核函数外，也可选择线性核函数、多项式核函数等等：

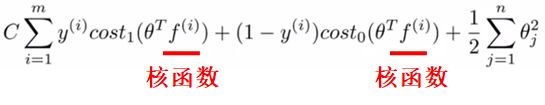
展开二者的结构发现，核函数也正好处于激活函数的位置构成了一个个类似于神经元的节点，θ矩阵也刚好相当于权重参数。放一张我很喜欢的图，出自博客：

https://blog.csdn.net/lyxleft/article/details/82880860

对比二者的权重参数θ发现，NN里θ是直接和特征数相关的，我图片是20*20大小，就有400个特征，但对于SVM来说，权重是和样本数量相关的，训练使用了多少个样本，每优化一次就要对多少个样本作比对，所以一般训练SVM使用的样本量会比较小。