吴恩达|机器学习作业6.0支持向量机(SVM)

6.0.支持向量机

1）题目：

在本练习中，您将使用支持向量机来建立一个垃圾邮件分类器。
在本练习的前半部分，您将使用支持向量机(SVM)处理各种两维的样本数据集。使用这些数据集进行实验将帮助您直观地了解支持向量机如何工作，以及如何使用带高斯核函数的SVM。在后半部分的练习中，您将使用支持向量机来构建垃圾邮件分类器。本次作业只包含前半部分。
数据集链接: https://pan.baidu.com/s/1cEgQIvehUcLxZ0WVhxcPuQ 提取码: xejn

2）知识点概括：

有人也称SVM为大间距分类器（large margin classifier）
带正则化的优化目标：${\min }_{\theta }C{\sum }_{i=1}^m[y^{(i)}cos{t}_1({\theta }^T{x}^{(i)})+(1-y^{(i)})cos{t}_0({\theta }^T{x}^{(i)})]+\frac{1}{2}{\sum }_{j=1}^n{\theta }_j^2$
假设函数：$h_{\theta }(x)=1if{\theta }^{T}x\ge 0else0$

核函数用来定义新的特征变量。将训练数据作为标记点，利用核函数计算每个训练数据与其他训练数据之间的相似度得到新的特征向量。这样，优化目标和假设函数变为：
${\min }_{\theta }C{\sum }_{i=1}^m[y^{(i)}cos{t}_1({\theta }^T{f}^{(i)})+(1-y^{(i)})cos{t}_0({\theta }^T{f}^{(i)})]+\frac{1}{2}{\sum }_{j=1}^m{\theta }_j^2$
$y=1if{\theta }^{T}f\ge 0$
核函数需要满足默塞尔定理（Mercer’s theorem）保证SVM优化运行正常，不会发散。

偏差与方差问题：
当C较大时：可能产生低偏差、高方差问题，过拟合
当C较小时：可能产生高偏差、低方差问题，欠拟合

对于高斯核函数中的方差sigma：
较大时：特征变化较缓，可能会产生高偏差、低方差问题，欠拟合
较小时：特征变化较快，可能产生低偏差、高方差问题，过拟合

待定的：
参数C的选择
核函数的选择

模型选择：
当特征数量多、训练集数量较少时，一般选用逻辑回归或者不带核函数的SVM（线性核函数）
当特征数量少、训练集数量适中时，一般选用带高斯核函数的SVM
当特征数量少、训练集数量很大时，一般选用逻辑回归或者不带核函数的SVM（如果用高斯核函数可能过慢）

对于大部分情况神经网络表现都很好，但是训练慢。
且SVM是凸优化问题，因此总会找到一个全局最小值，不用担心局部极小的情况。

逻辑回归与SVM比较：逻辑回归对异常值敏感，SVM对异常值不敏感(抗噪能力强)——支持向量机改变非支持向量样本并不会引起决策面的变化；但是逻辑回归中改变任何样本都会引起决策面的变化

3）大致步骤：

样本集1，首先可视化数据集，然后使用不同的C再用线性核函数的SVM训练模型并画出决策边界。
样本集2，可视化数据集，定义高斯函数，再使用高斯核SVM训练（这里我还没搞清楚自定义核函数的要求，所以直接用内置的高斯核训练模型，但是感觉不用了解，吴恩达说的一般也不会用很奇怪的核函数）
样本集3，可视化训练集和验证集，和样本集2一样采用高斯核函数，但是这里尝试不同的C和sigma，选择在验证集上错误率最低的模型，最后画出决策边界

4）关于Python：

• Scikit-learn(sklearn)是机器学习中常用的第三方模块，对常用的机器学习方法进行了封装，包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)、聚类(Clustering)等方法。里面包含了SVM的程序，直接调用调节参数即可。
• svm.SVC( ) 可以选择C值，以及核函数，调用之后先fit，再predict，注意predict时输入为一个二维数组，因此在画等高线的时候需要先把网格展开成二维数组进行predict再重新组成网格画图。在选择核函数时可以自己定义，例如：svm.SVC(kernel=my_kernel)，内置核函数默认为rbf高斯核，形式为$exp(-\gamma \Vert x-x^{\prime }{\Vert }^2)$，其中包含一个gamma关键词，gamma默认为1/n_features。
• 具体可参考sklearn中文文档：http://sklearn.apachecn.org/#/docs/5
• 在计算错误率时，可能会涉及两幅图像像素值之间的加减运算，这里需要注意的是图像像素值是ubyte类型，ubyte类型数据范围为0~255，若做运算出现负值或超出255，则会抛出异常，因此需要将预测的y值和yval强制转为int再进行相减。

5）代码与结果：

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio
from sklearn import svm 

data1 = scio.loadmat('ex6data1.mat')
data2 = scio.loadmat('ex6data2.mat')
data3 = scio.loadmat('ex6data3.mat')
x1 = data1['X']
y1 = data1['y'].flatten()
x2 = data2['X']
y2 = data2['y'].flatten()
x3 = data3['X']
y3 = data3['y'].flatten()
xval = data3['Xval']
yval = data3['yval'].flatten()

'''============================part1========================='''
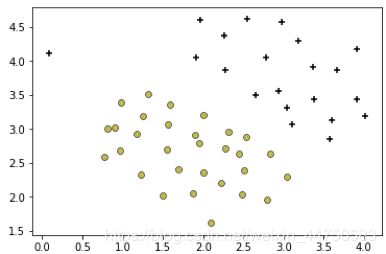
'''可视化数据集'''
def plot_data(x, y):
    p = x[y==1]
    n = x[y==0]
    plt.scatter(p[:,0], p[:,1], c='k', marker='+', label='y=1')
    plt.scatter(n[:,0], n[:,1], c='y', marker='o', edgecolors='k', linewidths=0.5, label='y=0')
    plt.show
  
plot_data(x1, y1)

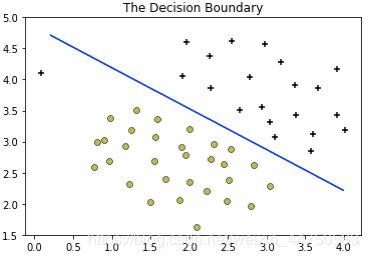
'''线性核函数模型-样本1'''
clf1 = svm.SVC(C=1, kernel='linear')
clf1.fit(x1, y1)
#clf1.predict([[2.0, 4.5]])


'''画出决策边界'''
def plot_boundary(clf, x1):
    u = np.linspace(np.min(x1[:,0]), np.max(x1[:,0]), 500) #为了后面可以直接调用这个函数
    v = np.linspace(np.min(x1[:,1]), np.max(x1[:,1]), 500)
    x, y = np.meshgrid(u, v) #转为网格（500*500）
    z = clf.predict(np.c_[x.flatten(), y.flatten()]) #因为predict中是要输入一个二维的数据，因此需要展开
    z = z.reshape(x.shape) #重新转为网格
    plt.contour(x, y, z, 1, colors='b') #画等高线
    plt.title('The Decision Boundary')
    plt.show
   
#画图   
plt.figure(1)
plot_data(x1, y1)
plot_boundary(clf1, x1)
plt.show

'''============================part2========================='''
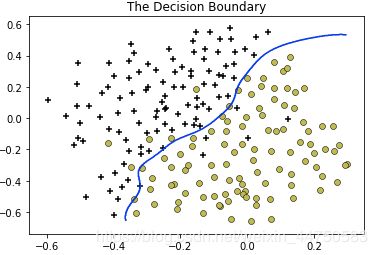
'''高斯核函数模型-样本2'''
#可视化训练集
plot_data(x2, y2) 

#定义高斯核函数
def gaussianKernel(x1, x2, sigma):
    return np.exp( -((x1-x2).T@(x1-x2)) / (2*sigma*sigma) )
    
a1 = np.array([1, 2, 1])    
a2 = np.array([0, 4, -1])  
sigma = 2
gaussianKernel(a1, a2, sigma) #检查是否为0.32465246735834974

#训练模型（这里使用内置高斯核）
clf2 = svm.SVC(C=1, kernel='rbf', gamma=np.power(0.1, -2)/2) #对应sigma=0.1
clf2.fit(x2, y2)
#clf2.predict([[0.4, 0.9]])

#画图   
plt.figure(2)
plot_data(x2, y2)
plot_boundary(clf2, x2)
plt.show

'''============================part3========================='''
'''高斯核函数模型-样本3'''
#可视化训练集
plot_data(x3, y3) 

plot_data(xval, yval) 

try_value = np.array([0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30])
#错误率
def error_rate(predict_y, yval):
    m = yval.size
    count = 0
    for i in range(m):
        count = count + np.abs(int(predict_y[i])-int(yval[i])) #避免溢出错误得到225
    return float(count/m)    

#模型选择
def model_selection(try_value, x3, y3, xval, yval):
    error = 1
    c = 1
    sigma = 0.01
    for i in range(len(try_value)):
        for j in range(len(try_value)):
            clf = svm.SVC(C=try_value[i], kernel='rbf', gamma=np.power(try_value[j], -2)/2)
            clf.fit(x3, y3)
            predict_y = clf.predict(xval) 
            if error > error_rate(predict_y, yval):
                error = error_rate(predict_y, yval)
                c = try_value[i]
                sigma = try_value[j]
    return c, sigma, error

c, sigma, error = model_selection(try_value, x3, y3, xval, yval) #(1.0, 0.1, 0.035)  


clf3 = svm.SVC(C=c, kernel='rbf', gamma=np.power(sigma, -2)/2)
clf3.fit(x3, y3)

#画图   
plt.figure(3)
plot_data(x3, y3)
plot_boundary(clf3, x3)
plt.show

样本集1可视化结果

C=1时的决策边界，比较合适的给出了间距

C=100时的决策边界，把异常点也正确分类了，可以看出C太大可能会过拟合

样本集2可视化结果，明显非线性可分

C=1、sigma=0.1时的决策边界

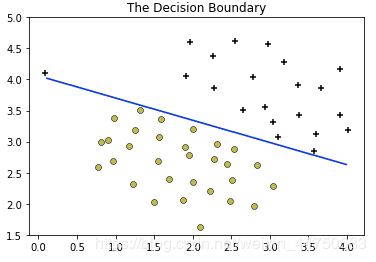
C=1、sigma=0.01时的决策边界，显然过拟合了，此时simga太小了

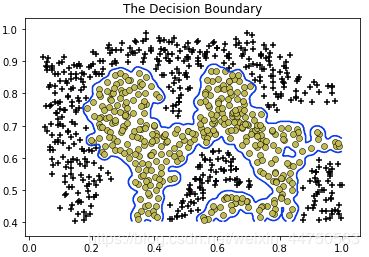
C=1、sigma=0.5时的决策边界，显然拟合的不好，欠拟合了，此时simga太大了

样本3选择出错误率最低的模型，即C=1, sigma=0.1, 错误率为0.035

此时的决策边界