机器学习实战python实例（2）SVM与核函数

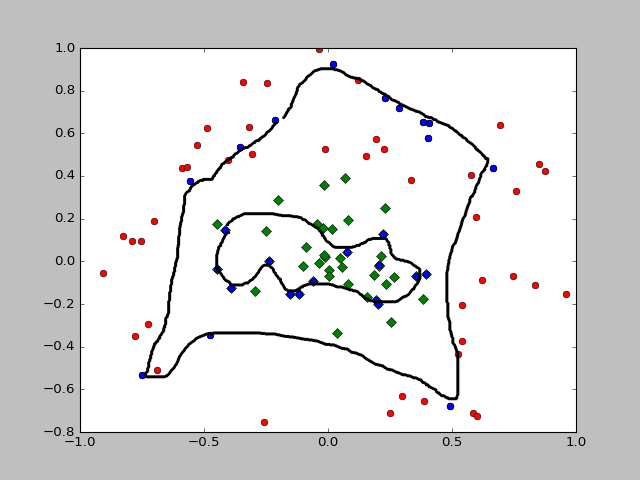
前两篇博客涉及到的SVM还只是一个线性分类器，如果在二维情况下遇到如下的情况，线性分类器的效果就不会很好了
这个时候我们就需要一个叫做核函数的东西，简单来说它的最大作用就是把低维数据映射到高维数据，具体可以看前面推荐的一篇文章http://www.thebigdata.cn/JieJueFangAn/12661.html中核函数的部分，这里借用两张图来演示效果

这样我们就能分割开了，一个比较通俗的理解是：一个物体当你一个属性无法描述清楚时，就多增加几个属性来描述它，在无限个属性之内总能够描述清楚，而如何增加属性来描述它呢，需要的是核函数。

在之前的代码中，我们相当于使用了线性核函数（X*Xi.T），而这次为了分类如图的数据，我们需要使用径向基函数得高斯版本
我们需要把之前涉及到线性核函数的部分替换掉，并且增加一部分用来计算和保存核函数
在前两篇的SVM.py中添加以下部分

def kernelTrans(X, A, kTup):
    m, n = shape(X)
    K = mat(zeros((m, 1)))
    if kTup[0] == 'lin':
        K = X * A.T
    elif kTup[0] == 'rbf':
        for j in xrange(m):
            deltaRow = X[j, :] - A
            K[j] = deltaRow * deltaRow.T
        K = exp(K / (-1 * kTup[1] ** 2))
    else:
        raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
    return K

在SVM.py中修改以下部分：

class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler, kTup):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m, 1)))
        self.b = 0
        self.eCache = mat(zeros((self.m, 2)))
        self.K = mat(zeros((self.m, self.m)))
        for i in xrange(self.m):
            self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)


def innerL(i, oS):
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C))\
            or ((oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
        j, Ej = selectJ(i, oS, Ei)
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        if oS.labelMat[i] != oS.labelMat[j]:
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L == H:
            print "L == H"
            return 0
        eta = 2.0 * oS.K[i, j] - oS.K[i, i] - oS.K[j, j]
        if eta >= 0:
            print "eta >= 0"
            return 0
        oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
        updateEk(oS, j)
        if abs(oS.alphas[j] - alphaJold) < 0.00001:
            print "j not moving enough"
            return 0
        oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
        updateEk(oS, i)
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] \
                - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[i, j]
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] \
                - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j, j]
        if 0 < oS.alphas[i] < oS.C:
            oS.b = b1
        elif 0 < oS.alphas[j] < oS.C:
            oS.b = b2
        else:
            oS.b = (b1 + b2) / 2.0
        return 1
    else:
        return 0


def calcEk(oS, k):
    fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k]) + oS.b
    Ek = fXk - float(oS.labelMat[k])
    return Ek

再加入一个函数来测试训练的分类器的效果

def testRbf(k1=1.3):
    dataArr, labelArr = loadDataSet("testSetRBF.txt")
    b, alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1))
    dataMat = mat(dataArr)
    labelMat = mat(labelArr).transpose()
    svInd = nonzero(alphas.A > 0)[0]
    sVs = dataMat[svInd]
    labelSV = labelMat[svInd]
    print "there are %d Support Vectors" % shape(sVs)[0]
    m, n = shape(dataMat)
    errorCount = 0
    for i in xrange(m):
        kernelEval = kernelTrans(sVs, dataMat[i, :], ('rbf', 1))
        predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
        if sign(predict) != sign(labelMat[i]):
            errorCount += 1
    print "the training error rate is: %f" % (float(errorCount) / m)

    dataArr, labelArr = loadDataSet("testSetRBF2.txt")
    dataMat = mat(dataArr)
    labelMat = mat(labelArr).transpose()
    m, n = shape(dataMat)
    errorCount = 0
    for i in xrange(m):
        kernelEval = kernelTrans(sVs, dataMat[i, :], ('rbf', 1))
        predict = kernelEval.T * multiply(labelSV, alphas[svInd]) + b
        if sign(predict) != sign(labelMat[i]):
            errorCount += 1
    print "the test error rate is: %f" % (float(errorCount) / m)

直接调用SVM.testRbf(),错误率在10%左右，为了方便我画出了支持向量

def showRBF(dataArr, labelArr, alphas):
    for i in xrange(len(labelArr)):
        if labelArr[i] == -1:
            plt.plot(dataArr[i][0], dataArr[i][1], 'or')
        elif labelArr[i] == 1:
            plt.plot(dataArr[i][0], dataArr[i][1], 'Dg')
    dataMat = mat(dataArr)
    svInd = nonzero(alphas.A > 0)[0]
    sVs = dataMat[svInd]
    for i in xrange(shape(sVs)[0]):
        plt.plot(dataArr[i][0], dataArr[i][1], 'ob')
    plt.show()

测试数据请下载http://download.csdn.net/detail/xiaonannanxn/9620023