机器学习笔记02——线性回归实践
摘要:本文将介绍机器学习中的线性回归。主要包括简单的线性回归和多元线性回归的简单代码实现。
目录
- 1.简单的线性回归
- 2.多元线性回归
- 3.用到的数据
- 4.全文总结
1.简单的线性回归
使用单一特征值来预测响应值,基于自变量x来预测因变量y的方法;x和y要是线性相关的,然后,我们来寻找一种更据特征值或自变量x的线性函数来精确预测响应值y。
找到最佳拟合线可以最小化预测误差;可通过最小化观测值Yi和模型预测值Yp之间的长度;
这里主要使用Sklearn里的LinearRegression算法:
代码:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
#数据预处理
dataset = pd.read_csv('studentscores.csv')
X = dataset.iloc[:,:1].values
Y = dataset.iloc[:,1]
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=1/4,random_state=0)
#训练模型
reg = LinearRegression()
reg = reg.fit(X_train,Y_train)
#预测结果
Y_pre = reg.predict(X_test)
#训练集结果可视化
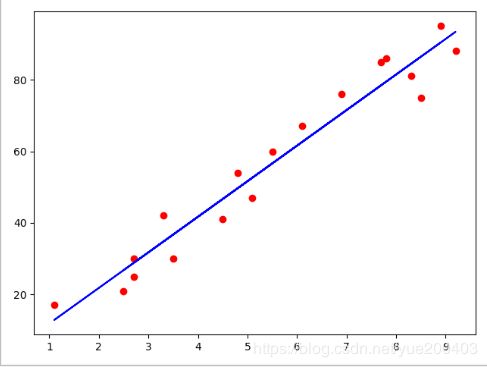
plt.scatter(X_train,Y_train,color='red')
plt.plot(X_train,reg.predict(X_train),color='blue')
plt.show()
#测试集结果可视化
plt.scatter(X_test,Y_test,color='red')
plt.plot(X_test,reg.predict(X_test),color='blue')
plt.show()
"""plot画点以后会用一条线串起来,而scatter只是单独的点而已"""
2.多元线性回归
代码:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import preprocessing
from sklearn.preprocessing import OneHotEncoder,StandardScaler
#数据预处理
dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[:,:-1].values
Y = dataset.iloc[:,4]
#将类别数据数字化
le = preprocessing.LabelEncoder()
X[:,3] = le.fit_transform(X[:,3])
oh = OneHotEncoder(categorical_features=[3])
X = oh.fit_transform(X).toarray()
#print(X[:,3])
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.2,random_state=0)
#训练模型
reg = LinearRegression()
reg = reg.fit(X_train,Y_train)
#预测结果
Y_pre = reg.predict(X_test)
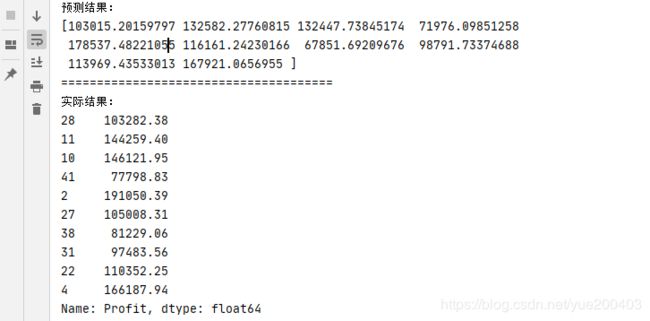
print("预测结果:")
print(Y_pre)
print("======================================")
print("实际结果:")
print(Y_test)
"""多元线性回归分析与简单线性回归很相似,但是要复杂一些了(影响因素由一个变成多个)。它有几个假设前提需要注意,
①线性,自变量和因变量之间应该是线性的
②同方差,误差项方差恒定
③残差负荷正态分布
④无多重共线性
OneHotEncoderone-hot编码是一种对离散特征值的编码方式,在LR模型中常用到,用于给线性模型增加非线性能力。
"""
"""
多元线性回归中还有虚拟变量和虚拟变量陷阱的概念
虚拟变量:分类数据,离散,数值有限且无序,比如性别可以分为男和女,回归模型中可以用虚拟变量表示,1表示男,0表示女。
虚拟变量陷阱:两个或多个变量高度相关,即一个变量一个变量可以由另一个预测得出。直观地说,有一个重复的类别:
如果我们放弃了男性类别,则它在女性类别中被定义为零(女性值为零表示男性,反之亦然)。 虚拟变量陷阱的解决方
案是删除一个分类变量 —— 如果有多个类别,则在模型中使用m-1。 遗漏的值可以被认为是参考值。
需要注意的是:变量并非越多越好,过多变量尤其是对输出没有影响的变量,可能导致模型预测精确度降低,
所以要选择合适的变量,主要方法有三种,①向前选择(逐次加使RSS最小的自变量)②向后选择(逐次扔掉p值最大的变量)③双向选择
"""
3.用到的数据
1.文件一:studentscores.csv
Hours,Scores
2.5,21
5.1,47
3.2,27
8.5,75
3.5,30
1.5,20
9.2,88
5.5,60
8.3,81
2.7,25
7.7,85
5.9,62
4.5,41
3.3,42
1.1,17
8.9,95
2.5,30
1.9,24
6.1,67
7.4,69
2.7,30
4.8,54
3.8,35
6.9,76
7.8,86
2.文件二:50_Startups.csv
R&D Spend,Administration,Marketing Spend,State,Profit
165349.2,136897.8,471784.1,New York,192261.83
162597.7,151377.59,443898.53,California,191792.06
153441.51,101145.55,407934.54,Florida,191050.39
144372.41,118671.85,383199.62,New York,182901.99
142107.34,91391.77,366168.42,Florida,166187.94
131876.9,99814.71,362861.36,New York,156991.12
134615.46,147198.87,127716.82,California,156122.51
130298.13,145530.06,323876.68,Florida,155752.6
120542.52,148718.95,311613.29,New York,152211.77
123334.88,108679.17,304981.62,California,149759.96
101913.08,110594.11,229160.95,Florida,146121.95
100671.96,91790.61,249744.55,California,144259.4
93863.75,127320.38,249839.44,Florida,141585.52
91992.39,135495.07,252664.93,California,134307.35
119943.24,156547.42,256512.92,Florida,132602.65
114523.61,122616.84,261776.23,New York,129917.04
78013.11,121597.55,264346.06,California,126992.93
94657.16,145077.58,282574.31,New York,125370.37
91749.16,114175.79,294919.57,Florida,124266.9
86419.7,153514.11,0,New York,122776.86
76253.86,113867.3,298664.47,California,118474.03
78389.47,153773.43,299737.29,New York,111313.02
73994.56,122782.75,303319.26,Florida,110352.25
67532.53,105751.03,304768.73,Florida,108733.99
77044.01,99281.34,140574.81,New York,108552.04
64664.71,139553.16,137962.62,California,107404.34
75328.87,144135.98,134050.07,Florida,105733.54
72107.6,127864.55,353183.81,New York,105008.31
66051.52,182645.56,118148.2,Florida,103282.38
65605.48,153032.06,107138.38,New York,101004.64
61994.48,115641.28,91131.24,Florida,99937.59
61136.38,152701.92,88218.23,New York,97483.56
63408.86,129219.61,46085.25,California,97427.84
55493.95,103057.49,214634.81,Florida,96778.92
46426.07,157693.92,210797.67,California,96712.8
46014.02,85047.44,205517.64,New York,96479.51
28663.76,127056.21,201126.82,Florida,90708.19
44069.95,51283.14,197029.42,California,89949.14
20229.59,65947.93,185265.1,New York,81229.06
38558.51,82982.09,174999.3,California,81005.76
28754.33,118546.05,172795.67,California,78239.91
27892.92,84710.77,164470.71,Florida,77798.83
23640.93,96189.63,148001.11,California,71498.49
15505.73,127382.3,35534.17,New York,69758.98
22177.74,154806.14,28334.72,California,65200.33
1000.23,124153.04,1903.93,New York,64926.08
1315.46,115816.21,297114.46,Florida,49490.75
0,135426.92,0,California,42559.73
542.05,51743.15,0,New York,35673.41
0,116983.8,45173.06,California,14681.4
4.全文总结
数据需要自己建一个csv文件,然后把上面的内容复制进去;多元线性回归并没有画结果预测图,看后期能不能补上。
参考资料:
微信公众号:机器学习算法与python实践
往期文章推荐:
机器学习笔记01——数据预处理
神经网络—用python实现异或运算详细解释