蓝桥杯 C/C++ 大学A组 2016年省赛真题之“方格填数”(全排列)
本文为武汉大学郑未《蓝桥杯历届真题解析》学习笔记。
添加链接描述
方格填数
(第三题)
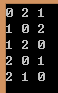
有如下十个方格:

**要求:**连续的两个数不能相邻。
(左右、上下、对角都算相邻)
求有多少种填法。
**考点:**全排列
- 如14年的扑克排序
A A 2 2 3 3 4 4,一共4对扑克牌,请把它们排成一列。
要求:两个A中间有1张牌,两个2中间有2张牌,两个3之间有3张牌,两个4之间有4张牌。
请写出符合要求的排列中,字典序最小的那个。 - 如2015年的手链样式
全排列+特殊去重
解法一:
使用递归来对0-9这10个数进行全排列,再检查排列的结果是否符合题目要求。
/*方格填数*/
#include 解法二:
用一个如下图所示的5*6的二维数组中间部分的空间来存储0-9的全排列,数组中的其他元素填-10(如图中填-1的那些单元格),这样对所有0-9的元素,都可用一个双重的for循环来检测其处于中心位置的九宫格中,是否存在数值与它是相连的。
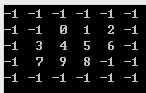
#include 解法三:
调用头文件中的next_permutation()函数来进行全排列操作,沿用解法二的check()操作。
/*方格填数*/
#include 注意点:
(1)每次check()数据不合格后,需要对所有已填入0-9的数组元素进行初始化,否则下次check()时,上次填入的元素会影响判断。我最开始没想到这个问题,最后输出的ans值为0。
(2)用next_permutation()函数对数组元素进行全排列时,需先将该数组中的元素按从小到大的顺序排好序,因为该函数默认当数组中元素降序排序时,全排列操作完成,退出执行。
next_permutation()用法示例:
#include 寒假作业
(第六题)
现在小学的数学题目也不是那么好玩的。
看看这个寒假作业:
□ + □ = □
□ - □ = □
□ × □ = □
□ ÷ □ = □
每个方块代表1~13中的某一个数字,但不能重复。
比如:
6 + 7 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
以及:
7 + 6 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
就算两种解法。(加法,乘法交换律后算不同的方案)
请问:你一共找到了多少种方案?
考点:对1-13个数进行全排列
解法一:
用递归进行全排列
#include 由于是对13个数进行全排列,程序运行较慢:

可增加一些检验条件,及时终止部分不合要求的排列,可对f函数稍作更改:
/*用递归实现全排列*/
void f(int k)
{
if(k==13){
if(check())
ans++;
}
int i,t;
for(i=k;i<13;++i){
{t=a[i];a[i]=a[k];a[k]=t;} //交换
if((k==2 && a[0]+a[1]!=a[2]) || (k==5 && a[3]-a[4]!=a[5]) ||(k==8 && a[6]*a[7]!=a[8])){
{t=a[i];a[i]=a[k];a[k]=t;} //如不合要求,撤销前一步的交换操作
continue;
}
f(k+1);
{t=a[i];a[i]=a[k];a[k]=t;} //回溯
}
}
另外,在这道题上我尝试用next_permutation()算法来进行全排列,运行结果很慢很慢。
又分析了上面next_permutation()进行全排列的规律(如下图),来增加适当的检验条件,程序没运行出来。可能是我的程序本身有问题,暂时将这个失败的程序记在这里。

#include 剪格子
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来,要求必须是连着的。
(仅仅连接一个角不算相连)
比如,下面两张图中,粉红色所示部分就是合格的剪取。
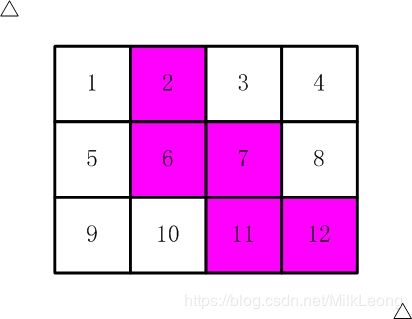
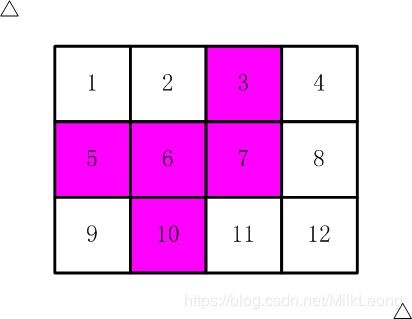
请你计算,一共有多少种不同的剪取方法。
此题与13年剪格子有相似之处,但那个题的限制条件是格子数值之和为总和的一半,此题限制只能是5个格子。
注意点:
单纯的dfs()无法解决T字型连通方案(不能同时往水平和垂直两个方向走)。
本题的解决方法是,找出任意5个格子,判断是否连通。
(1)从12个格子里面选出5个(全排列,但是是对重复的元素进行全排列)。
(2)在二维数组中检测连通性(经典问题),可用dfs快速解决。
解法一:
在对12个元素进行全排列后再检测其是否符合题目要求,运行较慢,运行时间为1300多秒。
/*剪格子:在排列之后再做重复性判断*/
#include
return 0;
}
下图是对代码中涉及的深度遍历的一个图示:
从一个非0的格子起,对它进行dfs,如果能走通(有相连为1者),将该格子置为0(标记访问过)

解法二:
抓取法
从12个元素中去抓取5个来构成path,是全排列的另一种方案,运行结果较快。
#include 解法三:
使用next_permutation()进行全排列。
#include