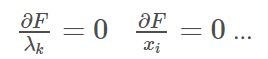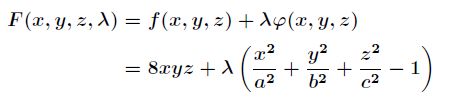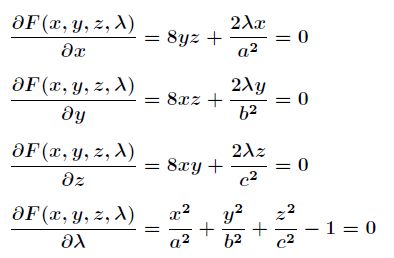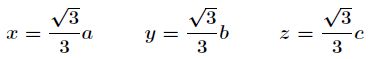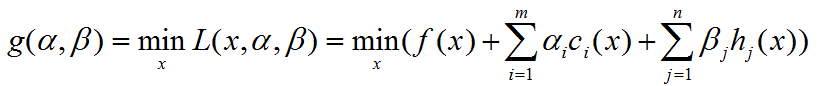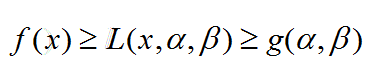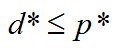拉格朗日乘子法 & KKT条件

目录

1. 拉格朗日乘子法用于最优化的原因

2. 最优化问题三种情况

2.1 无约束条件

2.2 等式约束条件：拉格朗日乘子法

2.3 不等式约束条件：KKT

3. Lagrange对偶函数

3.1 对偶函数与原问题的关系

3.2 Lagrange对偶问题

（1）弱对偶性

（2）强对偶性

（3）KKT条件

---

        在求解最优化问题中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）条件是两种最常用的方法，即：

• 拉格朗日乘子法：在有等式约束时使用拉格朗日乘子法；
• KKT条件：在有不等约束时使用KKT条件。

1. 拉格朗日乘子法用于最优化的原因

       考虑一个简单的问题目标函数f，等式约束，求解极小值点。

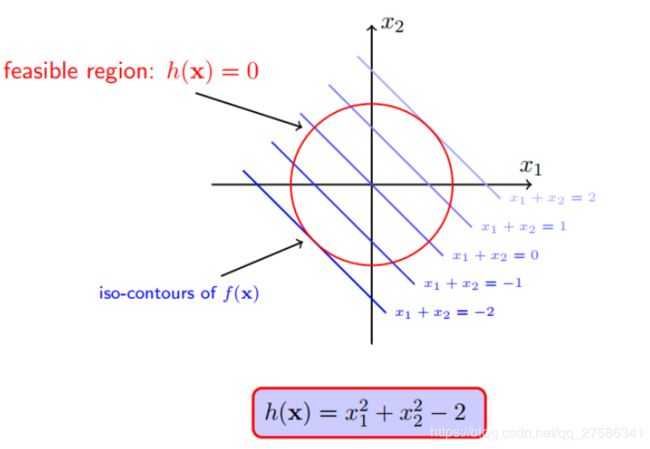
       f(x)在二维平面上画出等高线就是一条条斜率相同的直线，h(x)=0在二维平面上画出等高线就是一个圆，如下图所示。可以明显的看出，在圆圈h(x)的限制下，直线f(x)的最小值为-2，在左下角直线x1+x2=2和圆的交点上。

                                    

    （1）不考虑圆h(x)的限制时，f(x)要得到极小值，需要往f(x)的负梯度（下降最快的方向）方向走，如下左图蓝色箭头。

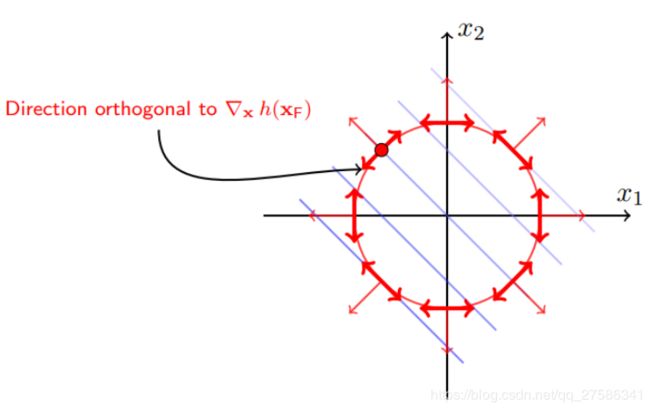
    （2）考虑圆h(x)的限制时，要得到极小值，需要沿着圆的切线方向走，如下右图红色粗箭头。注意这里的方向不是h(x)的梯度，而是正交于h(x)的梯度，h(x)梯度：右图的红色细箭头。在极小值点，f(x)和h(x)的等高线是相切的。

      

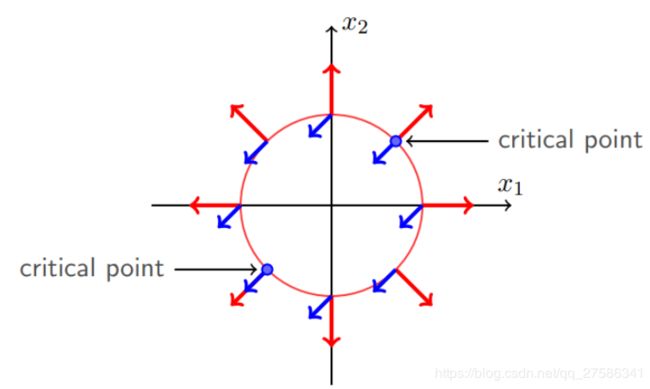
       容易发现，在关键的极小值点处，f(x)的负梯度和h(x)的梯度在同一直线上，如下图左下方critical point的蓝色和红色箭头所示。注意图中所示是同向的，但是这里并不一定是同向，有可能反向（因为等式约束h(x)=0，把h(x)变成-h(x)求解是一样的，这个时候h(x)的梯度就相反了）。

                                         

        由此可知，在极小值点，h(x)和f(x)的梯度在同一线上，有

                                                   

        所以，对于f(x)和h(x)而言，只要满足上面这个式子，同时使得h，解得的x就是我们要求的极小值点（或极大值点，为了简单起见我们只讨论极小值点）

        要做到这一点，可以构造一个拉格朗日函数，对函数令偏导等于0求解，恰好等价于“满足上面这个式子，同时使得h(x) = 0"，原问题转化为对拉格朗日函数求极值问题，这就是拉格朗日乘子法，如下图所示（注意一下这个μ的正负变化）。

                           

参考：拉格朗日乘子法和KKT条件

2. 最优化问题三种情况

　    我们这里提到的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值（因为最小值与最大值可以很容易转化，即最大值问题可以转化成最小值问题）。提到KKT条件一般会附带的提一下拉格朗日乘子。对学过高等数学的人来说比较拉格朗日乘子应该会有些印象。二者均是求解最优化问题的方法，不同之处在于应用的情形不同，KKT条件是对拉格朗日乘子法的一种泛化。

      一般情况下，最优化问题会碰到一下三种情况：

2.1 无约束条件

　　这是最简单的情况，解决方法通常是函数对变量求导，令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。

2.2 等式约束条件：拉格朗日乘子法

      设目标函数为f(x)，约束条件为h_k(x)，形如:

      s.t. 表示subject to ，“受限于”的意思，表示有个约束条件。

　　　　　　　               　

　　则解决方法是消元法或者拉格朗日法。消元法比较简单不在赘述，这里主要讲拉格朗日法，因为后面提到的KKT条件是对拉格朗日乘子法的一种泛化。

         拉格朗日乘子法的求解流程大概包括以下几个步骤： 
　　　  1）构造拉格朗日函数 
　　　  2）解变量的偏导方程 
　　　  3）代入目标函数即可 
 　 关键在于构造拉格朗日函数，后面求解实际上就是高数里面基本的求偏导数的问题了。我们不妨另：　                                   

                                                      

　　然后分别对每一个变量求导，得出来的解代入目标函数就ok了！

　                                         　

　　例如：求这个椭球的内接长方体的最大体积

        在条件

                                        

       下，求

                                    

       最大值。

       这个问题实际上就是条件极值问题，即在条件（1） 下，求的最大值。

　　当然这个问题实际可以先根据条件消去 z (消元法)，然后带入转化为无条件极值问题来处理。但是有时候这样做很困难，甚至是做不到的，这时候就需要用拉格朗日乘数法了。  

　　  首先定义拉格朗日函数F(x)：

　　　　　　　　  （ 其中λk是各个约束条件的待定系数。）                                                           

        然后解变量的偏导方程：

      　　　                              　......,

　　　如果有个约束条件，就应该有+1个方程。求出的方程组的解就可能是最优化值（高等数学中提到的极值），将结果带回原方程验证就可得到解。

　　　回到上面的题目，通过拉格朗日乘数法将问题转化为

　　　　     

　　　对求偏导得到

     　　　  

　　　联立前面三个方程得到和，带入第四个方程解之

　　　　      

　　　带入解得最大体积为：

      　　　　

 

2.3 不等式约束条件：KKT

       设目标函数f(x)，不等式约束为g(x)，有的教程还会添加上等式约束条件h(x)。此时的约束优化问题描述如下：

　　　　　　　　

        则我们定义不等式约束下的拉格朗日函数L，即广义拉格朗日函数：

　　　　　　　　

     其中，、是拉格朗日乘子，f(x)是原目标函数，hj(x)是第j个等式约束条件，λj是对应的约束系数，gk是不等式约束，uk是对应的约束系数。

　　常用的方法是KKT条件，同样地，把所有的不等式约束、等式约束和目标函数全部写为一个式子L(a, b, x)= f(x) + a*g(x)+b*h(x)，

　　KKT条件是说最优值必须满足以下条件：

　　　　（1）        原约束

　　　　（2） 

　　　　（3） 

　　求取这些等式之后就能得到候选最优值。其中第三个式子非常有趣，因为g(x)<=0，如果要满足这个等式，必须a=0或者g(x)=0. 这是SVM的很多重要性质的来源，如支持向量的概念。

　　基于KKT条件，不等式约束条件的问题基本也就解决了，下面来说说我自己的一点心得吧！ 
第一点：拉格朗日乘子法求解优化问题是很有效的方法，对于限制条件比较多的情况下，特别是限制条件较为复杂的情况下，利用该方法可以很容易的求解出来。 
第二点：约束条件其实就是限定了问题的解决范围，学会如何转化和考量限制条件是解决问题的关键。 
第三点：基础知识的重要性，比如说高数如果学不好的话。

3. Lagrange对偶函数

       在约束优化问题中，常常用拉格朗日对偶性来将原始问题转为对偶问题，通过解对偶问题的解来得到原始问题的解。

3.1 为什么要利用对偶？

首先要明确，对偶问题的解不一定直接等于原问题的解（弱对偶），但是，对偶问题有两点性质。

      （1） 满足某些条件时，对偶问题直接等于原问题的解（强对偶）

      （2）无论原始问题是否是凸的，对偶问题都是凸优化问题

显然，在某些情况下，直接对对偶问题求解可以得到原问题的解，而且对偶问题是凸优化，易于求解。所以利用对偶来求解是很有用的。

3.2 对偶函数与原问题的关系

（1）原始问题：

       假设f(x),ci(x),hj(x)是定义在Rn上的联系可微函数，考虑约束条件下最优化问题：

                                             

称此约束最优化问题为原问题。

（2）广义拉格朗日函数

                                        

（3）Lagrange对偶函数：

       定义拉格朗日对偶函数或者对偶函数g为拉格朗日函数关于x取得的最小值，即对α、β，有：

                    

通俗理解就是每确定一组(α，β)，就要找到一个x使得L最小，不同的(α，β)对应不同的g函数值。

（4）对偶函数与原问题的关系：

                                                      

        所以对偶函数是原问题的最优值下界，虽然不等式成立，但是如果α<0，并且让α趋近于负无穷，这个时候g(α,β)=-∞，虽然也满足不等式，但是此时没有任何意义。所以只有当α≥0，这个时候g(α,β)＞-∞时，对偶函数才能给出原目标函数一个非平凡有意义的下界，称此条件下的(α,β)是对偶可行的。图示如下：

                                        

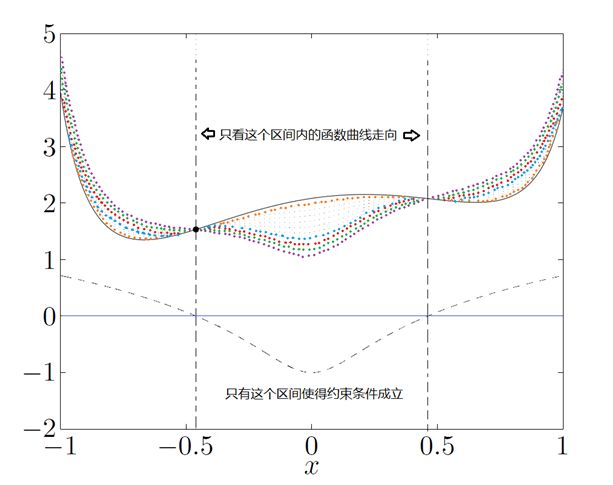
        在图中，实线——代表的是目标函数f(x)，虚线——代表的是约束条件c(x)，彩色的点线——代表λ取不同值的时候对应的拉格朗日函数L。我们可以看到，在约束条件可行(c(x)≤0)的区间内，拉格朗日函数都是小于目标函数的。在可行区间内，目标函数的最值将在x = -0.46处取得p∗=1.54。

为什么对偶函数一定是凹函数呢？

       其实L可以理解为一个以固定x带入c(x)和h(x)作为常数值系数，α、β作为变量的仿射函数。所谓仿射函数，就是f(x)=a*x+b形式，其实就是线性函数了。

       所以，g(α,β)为很多个仿射函数的逐个x取值点取最小值：

                        L=Aα+Bβ+C      其中：A=c(x)    B=h(x)    C=f(x)

      例如：L=2α+3β+1，L=α+2β+4， L=5α+β+3等等。

便于理解，先不考虑β，这样大致展示的图像就是如下：

                                      

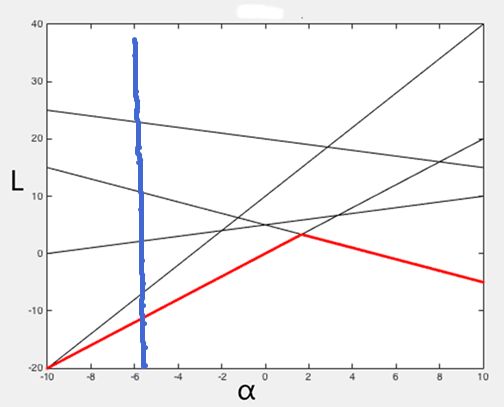
       里面的每一条直线，都是以某一固定x作为系数，α作为变量的线性函数的直线，也就是当x固定时候，随着α的变化，L的值不断发生变化。

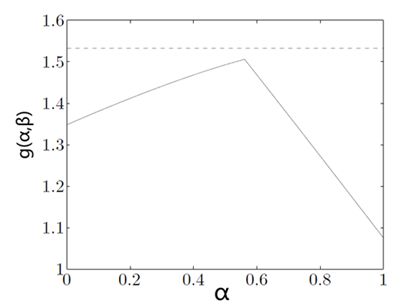
       当我们沿着L所在轴竖着切下来的时候，也就是图中个蓝色线，这个时候其实就是α固定，而对应不同的x情况下，L值的一个变化范围。由图可知，红色线就是每次固定α，而找到一个x，使得L最小的走势线，也就是g(α,β)的函数曲线，如下图：

                                               

       凹折线就是g(α,β)的曲线，水平虚线就是原问题的最优函数值P*。由此可知，无论原问题和约束条件是什么样的，对偶函数都是凹函数，且都小于等于原问题最优值。

3.3 Lagrange对偶问题

                                  

       对于任意一组(α，β)，其中α≥0，拉格朗日对偶函数给出了原问题的最优值的一个下界，因此，我们可以得到和参数α、β相关的一个下界。一个自然问题是：从Lagrange函数能得到的最好下界是什么？可以将这个问题表述为优化问题：

                                                                        

上述问题就称之为Lagrange对偶问题。

        前面讲只有当α≥0，g(α,β)＞-∞时此时才有意义，满足这样一组条件的(α，β)是上述对偶问题的一个可行解。如果一个解（α*，β*)是上述对偶问题的最优解，则称解(α*，β*)是对偶最优解或者最优Lagrange乘子。

此时对偶问题是一个凸优化问题，这是因为极大化目标函数是一个凹函数，且约束集合是一个凸集。

（1）弱对偶性

       Lagrange对偶问题的最优值，我们用*表示，根据定义，这是通过Lagrange函数得到的原问题最优值*的最好下界。特别地，我们有下面简单但是非常重要的不等式

                                                                     

即使原问题不是凸问题，上述不等式也成立，这个性质称为弱对偶性。

（2）强对偶性

        与弱对偶性相对应的有一个强对偶性（strong duality） ，强对偶即满足：

                                                                       

       强对偶是一个非常好的性质，因为在强对偶成立的情况下，可以通过求解对偶问题来得到原始问题的解，在 SVM 中就是这样做的。当然并不是所有的对偶问题都满足强对偶性 ，在 SVM 中是直接假定了强对偶性的成立，其实只要满足一些条件，强对偶性是成立的，比如说 Slater 条件与KKT条件。

（3）KKT条件

       假设x*是原始问题的最优解，α*和β*是对偶问题的最优解。如果强对偶成立，那么原问题最优解和对偶问题最优解必须满足KKT条件，属于充分必要条件。

                   

 

参考：

拉格朗日对偶理解：https://www.cnblogs.com/gczr/p/10521551.html