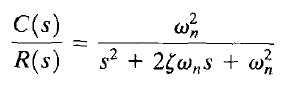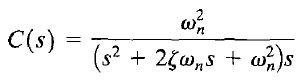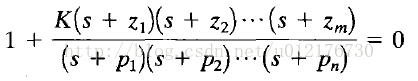现代控制系统-基于MATLAB和根轨迹的滞后超前校正

基于根轨迹的滞后超前校正技术以及MATLAB仿真

总结：

本文采用根轨迹法对开环传函进行补偿校正，最终使得校正后的开环传函在形成闭环后能够得到满足实际应用的时域响应（一般是单位阶跃响应和单位斜坡响应）。

关键字：

阻尼比，无阻尼自然频率，静态误差，最小相位系统

 

一般理论（源于现代控制工程（第五版））：

1.     二阶系统是一个更加典型的控制系统，一般高阶的系统都可以将其转化为一个或者多个二阶系统的和（线性系统的可加性），也就是说高阶系统的对输入的响应和以分解为众多二阶系统的响应的和；

2.     最小相位系统，我们假设我们的控制系统的所有零点和极点都在S平面的左半轴，也就是所有的零点、极点的实数部分小于等于0。

 

一般的二阶系统的标准形式：

（1）

其中ζ代表系统的阻尼比，ω_n为无阻尼自然频率。

三种情况：

1.     欠阻尼情况0<ζ<1，在这种情况下，如果R(s)输入为阶跃响应，那么C(s)可以写为：

（2）

其拉普拉斯反变换可以表示为：

（3）

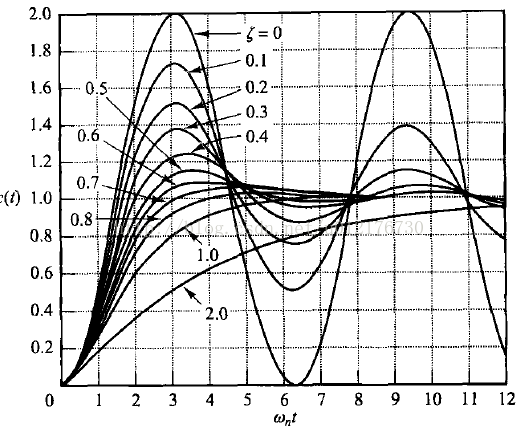
由上式可以看到，系统的阶跃响应包含了一个指数衰减与一个正弦函数的乘积，换句话说就是阶跃响应中有一个幅度逐渐衰减到0的正弦振荡。一种指数部分的衰减速率和阻尼比ζ和ω_n有关，且如果ω_n不变的情况下，ζ完全控制住了指数衰减的时间，这也就决定了该阶跃响应中正弦振荡的持续时间（影响系统的输出的稳定时间）；另一方面，正弦振荡的频率是由来ω_d控制，而ω_d就是；综合的来看，欠阻尼系统的阶跃响应是ζ和ω_n共同作用下形成的，所以将ζ称之为系统的阻尼比，ω_n为无阻尼自然频率；此时的传函的极点是一对共轭复数，其实数部分为复数；

而当ζ为0时，阶跃响应也是同上式（3）一样，只是此时的指数部分固定为常数，而正弦振荡部分却依旧存在，且会一直保持等幅振荡。

 

2.     临界阻尼情况ζ=1

此时，阶跃响应输出为：

（4）

可以看到原先欠阻尼情况下的正弦震荡部分已经消失，只剩下指数衰减部分；

此时的传函的极点是一个负实数；

3.     过阻尼情况1<ζ

此时的阶跃响应输出为：

（5）

可以看到，此时的阶跃响应输出为两个指数衰减的叠加，那是因为此时的传函的极点是两个负实数；

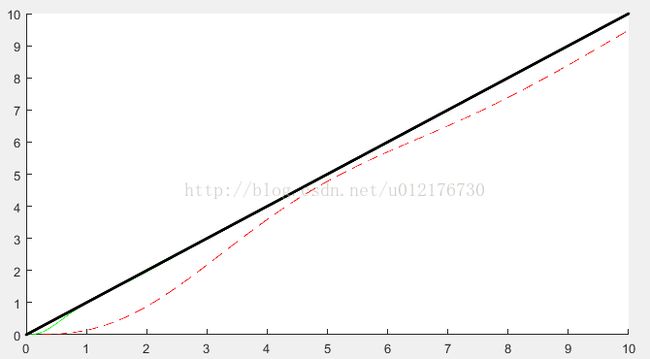
Figure1

不同ζ所对应的时域阶跃响应

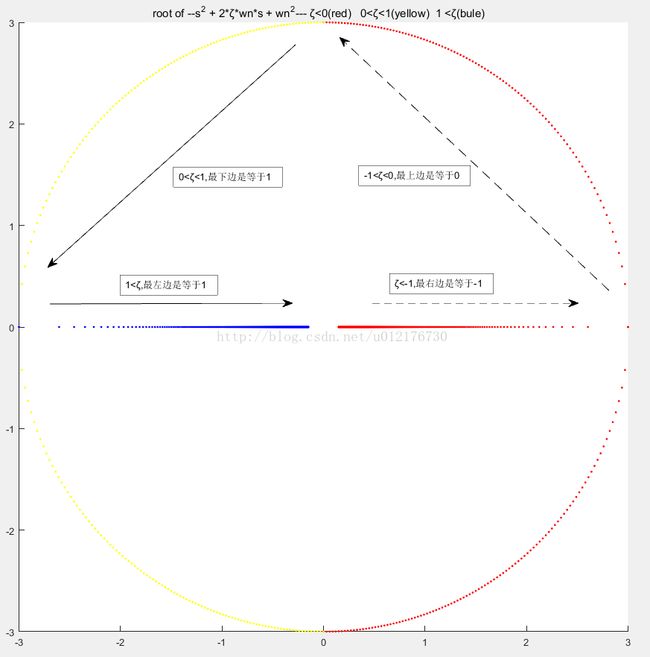
总结，实际上ζ所代表系统的阻尼比与ω_n所代表的无阻尼自然频率地大小共同决定了传函的极点的分布。

上图是不同的ζ的传函极点的分布图，其中红线部分代表ζ<0，此时的系统是发散或者震荡的，是不稳定的；黄线部分是衰减震荡（欠阻尼）；蓝线部分是不震荡（过阻尼）；因此，传函的极点实际上就决定了时域部分的响应：阶跃响应、斜坡响应等；

 

Figure2

 

 

 

根轨迹：根轨迹上的每一组点，实际上就是特征方程1+G(s)H(s)= 0的特征根，也就是：

(6)

影响特性根的因素有：

1.     开环传函G(s)H(s)本身的固有零点和极点；

2.     增益K；

所以特征根Root = F（zero，pole，K），也就是说，一个闭环传函具备怎样的极点，就是由开环传函的零、极点，以及K三者共同决定的。

超前校正：

一个闭环传函的瞬态响应，大致由闭环传函的主导极点来确定的。想换句话说，实现瞬态响应（ζ，ω_n）其实就是为了得到某个闭环极点Root。

1.     开环传函的zero，pole确定了，那么就只能通过调节K来得到Root；

2.     一旦我们期望的Root无法通过调节K得到时，那就必须通过增加额外的Zero’和Pole’，使得在某一个K下，能够得到预期的Root；

上述过程就是超前校正，目的就是为了实现瞬态响应的指标！

滞后校正：

除了瞬态响应的要求外，部分系统还会有静态误差的要求，这是就需要滞后校正。通过将放置靠近原点一对零、极点，滞后补偿后的根轨迹和补偿前的变化会非常小，但是却加大了Kv，也就是增大了静态速度误差常数，减少了静态速度误差，加强对输入信号的跟踪能力。

超前滞后校正一般过程：

目标时域响应特征（阻尼比和无阻尼自然频率）àà闭环传函极点àà计算得到辐角缺额 àà得到超前补偿用的零点和极点àà根据幅度条件得到Kcàà根据目标Kv，得到滞后补偿的零、极点àà完成

 

 

实例说明，利用超前补偿实现瞬态响应的控制

设计输入：G(s),H(s)=1;

设计目标：ζ=0.5，ω_n=5，Kv=80

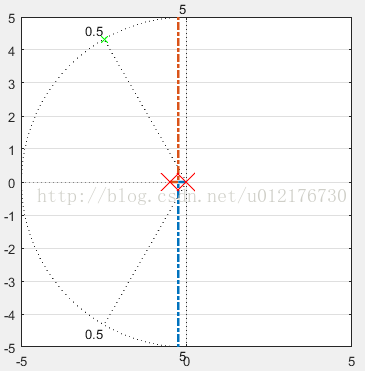
超前校正设计目标分解：ζ=0.5，ω_n=5，即需要一个闭环极点为-2.5+4.33i，此时未补偿闭环传函的根轨迹就是如下图虚线所示：

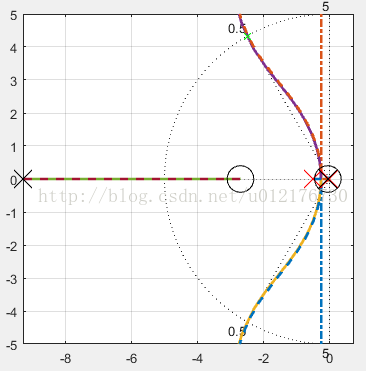
Figure3红×是开环极点，点虚线是未补偿的闭环根轨迹，绿色x目标闭环极点

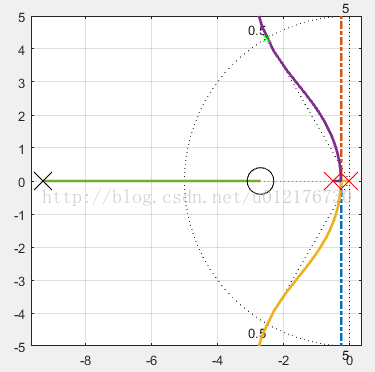
通过观察根轨迹，很明显通过调节K无法实现目标闭环极点（即根轨迹没有通过目标极点），那么只能通过增加零点和极点使其通过目标极点。后文会给出实现的算法，这里直接给出效果

Figure4 补偿后的根轨迹（实线）以及超前补偿器的零点和极点（黑x和黑o）

由上图可以看到，经过补偿后（上图中实轴上的多出来的黑色零极点），根轨迹已经被矫正了，可以看到它已经通过我们目标的极点：-2.5+4.33i以及Kc这意味着超前校正的目的完成，再来看一下校正前后的时域响应：

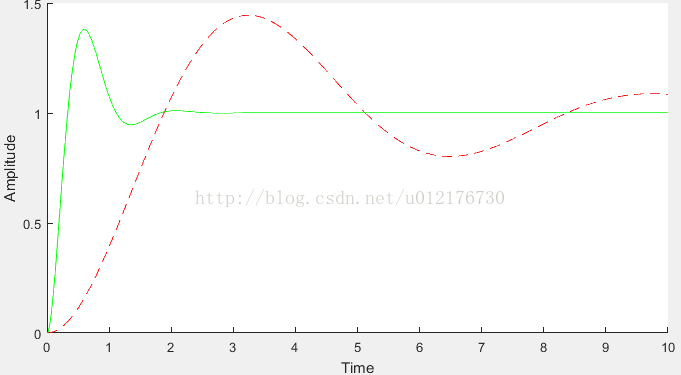
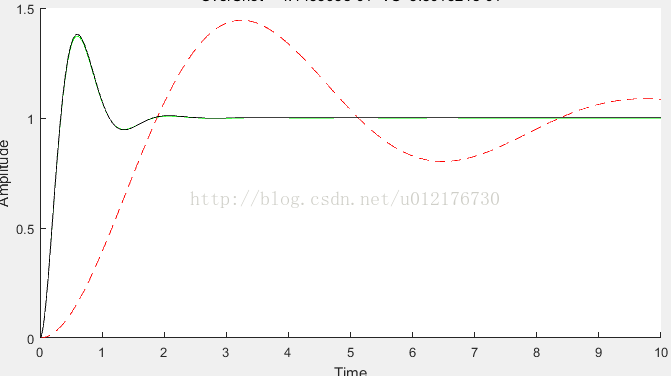
Figure5 红虚线是未补偿的闭环阶跃响应，绿线实线是补偿后的闭环阶跃响应

通过观察阶跃响应可以看到，超前补偿后的系统拥有更快的收敛速度，是满足我们实际应用的。

接下来可以利用滞后补偿，来调整稳态响应-静态速度误差Kv，实现的算法在后文，最终是在原点附近增加一对零、极点：

Figure6 在原点附近加入了新的零点和极点以及其根轨迹（双虚线）

利用滞后校正，实际上就是在原点附近增加一对零、极点，这一对零极点的目的是为了增加静态速度误差Kv，使得拥有更小的误差，同时不影响根轨迹，从而不影响瞬态响应。这个可以从下图的斜坡响应看出来：

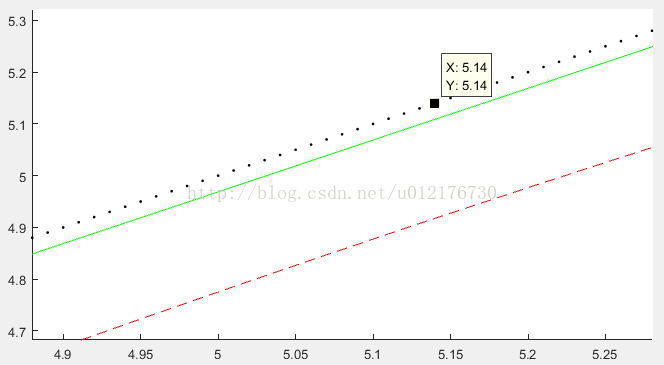
Figure 7 红线是未补偿的ramp响应，绿线是只经过超前补偿的响应，黑线是滞后超前补偿的响应

Figure 8 将上图部分区域放大，可以看到黑线比绿线相比拥有更少的静态速度误差（因为经过滞后校正后，Kv会更大）

但是此时的阶跃响应实际上没有太明显的变化，因为根轨迹并没有明显的被改变。

Figure 9 红线是未补偿的step响应，绿线是只经过超前补偿的响应，黑线是滞后超前补偿的响

 

校正完成。

 

算法

function [TransFunctionOfLeadCalibrater , TransFunctionOfLagCalibrater ] = LeadLagCalibrate_type1(TransFunctionOfOpenLoop,Zeta,Delta,Kv)


NumOpenLoop = TransFunctionOfOpenLoop.Numerator{1} ;     %开环传函的分子多项式
DenOpenLoop = TransFunctionOfOpenLoop.Denominator{1};    %开环传函的分母多项式


%根据Zeta和Delta可以得到目标闭环主极点的位置
Pole = -Zeta*Delta+sqrt(1-Zeta^2)*Delta*i;
%计算辐角缺额，先计算开环传函在目标极点处的值
ValueOfOpenLoopAtPole = polyval(NumOpenLoop,Pole)/polyval(DenOpenLoop,Pole);
%取这个值的角度信息
PhaseOfOpenLoopAtPole = angle(ValueOfOpenLoopAtPole);
%算得辐角缺额加上该角度值=±pi*(2k+1)
PhaseLoss = pi - PhaseOfOpenLoopAtPole
%计算目标极点到原点之间的角度
PhaseOfPoleToO = angle(Pole);
%然后得到用来补偿的零点和极点
PhaseOfCalibratedZeroToPole=(PhaseOfPoleToO+PhaseLoss)/2;
PhaseOfCalibratedPoleToPole=(PhaseOfPoleToO-PhaseLoss)/2; 


ZeroOfCalibrater = real(Pole)-(imag(Pole)/tan(PhaseOfCalibratedZeroToPole));
PoleOfCalibrater = real(Pole)-(imag(Pole)/tan(PhaseOfCalibratedPoleToPole));


%得到没有Kc的补偿器的分子和分母多项式
NumLeadCalibraterNoKc = [1 -ZeroOfCalibrater];
DenLeadCalibraterNoKc = [1 -PoleOfCalibrater];


%将极点代入上述多项式，使其满足幅值条件
ValueOfLeadCalibraterNoKcAtPole = polyval(NumLeadCalibraterNoKc,Pole)/polyval(DenLeadCalibraterNoKc,Pole);
KcOfLeadCalibrater = abs(1/(ValueOfLeadCalibraterNoKcAtPole*ValueOfOpenLoopAtPole));


%得到有Kc的补偿器的分子和分母多项式
NumLeadCalibrater = [KcOfLeadCalibrater -ZeroOfCalibrater*KcOfLeadCalibrater];
DenLeadCalibrater = [1 -PoleOfCalibrater];



% KvTransFunction = tf([conv(NumLeadCalibrater,NumOpenLoop),0],conv(DenLeadCalibrater,DenOpenLoop));
KvTransFunctionAtZeroAft = polyval([conv(NumLeadCalibrater,NumOpenLoop),0],0.00001)/polyval(conv(DenLeadCalibrater,DenOpenLoop),0.00001);
Beta = Kv/abs(KvTransFunctionAtZeroAft);


%得到没有Kc的滞后补偿器的分子和分母多项式
ZeroTemp = -0.05;
NumLagCalibraterNoKc = [1 -ZeroTemp];
DenLagCalibraterNoKc = [1 -ZeroTemp/Beta];




% ValueOfLagCalibraterNoKcAtZero = polyval(NumLagCalibraterNoKc,0)/polyval(DenLagCalibraterNoKc,0);
% KcOfLagCalibrater = abs(1/(Beta*KcOfLeadCalibrater*ValueOfLeadCalibraterNoKcAtPole*ValueOfOpenLoopAtPole))
TransFunctionOfLeadCalibrater = tf(NumLeadCalibrater,DenLeadCalibrater);
TransFunctionOfLagCalibrater = tf(NumLagCalibraterNoKc,DenLagCalibraterNoKc);