Torch7 - Tensor

The Tensor class is probably the most important class in Torch. Almost every package depends on this class. It is theclass for handling numeric data. As with pretty much anything in Torch7, tensors are serializable.

Multi-dimensional matrix

A Tensor is a potentially multi-dimensional matrix. The number of dimensions is unlimited that can be created usingLongStorage with more dimensions.

Example:

 --- creation of a 4D-tensor 4x5x6x2
 z = torch.Tensor(4,5,6,2)
 --- for more dimensions, (here a 6D tensor) one can do:
 s = torch.LongStorage(6)
 s[1] = 4; s[2] = 5; s[3] = 6; s[4] = 2; s[5] = 7; s[6] = 3;
 x = torch.Tensor(s)

The number of dimensions of a Tensor can be queried by nDimension() or dim(). Size of the i-th dimension is returned by size(i). A LongStorage containing all the dimensions can be returned by size().

> x:nDimension()
6
> x:size()
 4
 5
 6
 2
 7
 3
[torch.LongStorage of size 6]

Internal data representation

The actual data of a Tensor is contained into a Storage. It can be accessed using storage(). While the memory of aTensor has to be contained in this unique Storage, it might not be contiguous: the first position used in the Storage is given by storageOffset() (starting at 1). And the jump needed to go from one element to another element in the i-thdimension is given by stride(i). In other words, given a 3D tensor

x = torch.Tensor(7,7,7)

accessing the element (3,4,5) can be done by

> x[3][4][5]

or equivalently (but slowly!)

> x:storage()[x:storageOffset()
              +(3-1)*x:stride(1)+(4-1)*x:stride(2)+(5-1)*x:stride(3)]

One could say that a Tensor is a particular way of viewing a Storage: a Storage only represents a chunk of memory, while the Tensor interprets this chunk of memory as having dimensions:

x = torch.Tensor(4,5)
s = x:storage()
for i=1,s:size() do -- fill up the Storage
  s[i] = i
end
> x -- s is interpreted by x as a 2D matrix
  1   2   3   4   5
  6   7   8   9  10
 11  12  13  14  15
 16  17  18  19  20
[torch.DoubleTensor of dimension 4x5]

Note also that in Torch7 elements in the same row [elements along the last dimension] are contiguous in memory for a matrix [tensor]:

x = torch.Tensor(4,5)
i = 0

x:apply(function()
  i = i + 1
  return i
end)

> x
  1   2   3   4   5
  6   7   8   9  10
 11  12  13  14  15
 16  17  18  19  20
[torch.DoubleTensor of dimension 4x5]

> x:stride()
 5
 1  -- element in the last dimension are contiguous!
[torch.LongStorage of size 2]

This is exactly like in C (and not Fortran).

Tensors of different types

Actually, several types of Tensor exists:

ByteTensor -- contains unsigned chars
CharTensor -- contains signed chars
ShortTensor -- contains shorts
IntTensor -- contains ints
LongTensor -- contains longs
FloatTensor -- contains floats
DoubleTensor -- contains doubles

Most numeric operations are implemented only for FloatTensor and DoubleTensor. Other Tensor types are useful if you want to save memory space.

Default Tensor type

For convenience, an alias torch.Tensor is provided, which allows the user to write type-independent scripts, which can then ran after choosing the desired Tensor type with a call like

torch.setdefaulttensortype('torch.FloatTensor')

See torch.setdefaulttensortype for more details. By default, the alias "points" on torch.DoubleTensor.

Efficient memory management

All tensor operations in this class do not make any memory copy. All these methods transform the existing tensor, or return a new tensor referencing the same storage. This magical behavior is internally obtained by good usage of the stride() andstorageOffset(). Example:

x = torch.Tensor(5):zero()
> x
0
0
0
0
0
[torch.DoubleTensor of dimension 5]
> x:narrow(1, 2, 3):fill(1) -- narrow() returns a Tensor
                            -- referencing the same Storage as x
> x
 0
 1
 1
 1
 0
[torch.Tensor of dimension 5]

If you really need to copy a Tensor, you can use the copy() method:

y = torch.Tensor(x:size()):copy(x)

Or the convenience method

y = x:clone()

We now describe all the methods for Tensor. If you want to specify the Tensor type, just replace Tensor by the name of the Tensor variant (like CharTensor).

Tensor constructors

Tensor constructors, create new Tensor object, optionally, allocating new memory. By default the elements of a newly allocated memory are not initialized, therefore, might contain arbitrary numbers. Here are several ways to construct a newTensor.

torch.Tensor()

Returns an empty tensor.

torch.Tensor(tensor)

Returns a new tensor which reference the same Storage than the given tensor. The size, stride, and storage offset are the same than the given tensor.

The new Tensor is now going to "view" the same storage as the given tensor. As a result, any modification in the elements of the Tensor will have a impact on the elements of the given tensor, and vice-versa. No memory copy!

x = torch.Tensor(2,5):fill(3.14)
> x
 3.1400  3.1400  3.1400  3.1400  3.1400
 3.1400  3.1400  3.1400  3.1400  3.1400
[torch.DoubleTensor of dimension 2x5]

y = torch.Tensor(x)
> y
 3.1400  3.1400  3.1400  3.1400  3.1400
 3.1400  3.1400  3.1400  3.1400  3.1400
[torch.DoubleTensor of dimension 2x5]

y:zero()
> x -- elements of x are the same as y!
0 0 0 0 0
0 0 0 0 0
[torch.DoubleTensor of dimension 2x5]

torch.Tensor(sz1 [,sz2 [,sz3 [,sz4]]]])

Create a tensor up to 4 dimensions. The tensor size will be sz1 x sz2 x sx3 x sz4.

torch.Tensor(sizes, [strides])

Create a tensor of any number of dimensions. The LongStorage sizes gives the size in each dimension of the tensor. The optional LongStorage strides gives the jump necessary to go from one element to the next one in the each dimension. Of course, sizes and strides must have the same number of elements. If not given, or if some elements of strides arenegative, the stride() will be computed such that the tensor is as contiguous as possible in memory.

Example, create a 4D 4x4x3x2 tensor:

x = torch.Tensor(torch.LongStorage({4,4,3,2}))

Playing with the strides can give some interesting things:

x = torch.Tensor(torch.LongStorage({4}), torch.LongStorage({0})):zero() -- zeroes the tensor
x[1] = 1 -- all elements point to the same address!
> x
 1
 1
 1
 1
[torch.DoubleTensor of dimension 4]

Note that negative strides are not allowed, and, if given as argument when constructing the Tensor, will be interpreted as //choose the right stride such that the Tensor is contiguous in memory//.

Note this method cannot be used to create torch.LongTensors. The constructor from a storage will be used:

a = torch.LongStorage({1,2}) -- We have a torch.LongStorage containing the values 1 and 2
-- General case for TYPE ~= Long, e.g. for TYPE = Float:
b = torch.FloatTensor(a)
-- Creates a new torch.FloatTensor with 2 dimensions, the first of size 1 and the second of size 2
> b:size()
 1
 2
[torch.LongStorage of size 2]

-- Special case of torch.LongTensor
c = torch.LongTensor(a)
-- Creates a new torch.LongTensor that uses a as storage and thus contains the values 1 and 2
> c
 1
 2
[torch.LongTensor of size 2]

torch.Tensor(storage, [storageOffset, sizes, [strides]])

Returns a tensor which uses the existing Storage storage, starting at position storageOffset (>=1). The size of each dimension of the tensor is given by the LongStorage sizes.

If only storage is provided, it will create a 1D Tensor viewing the all Storage.

The jump necessary to go from one element to the next one in each dimension is given by the optional argumentLongStorage strides. If not given, or if some elements of strides are negative, the stride() will be computed such that the tensor is as contiguous as possible in memory.

Any modification in the elements of the Storage will have an impact on the elements of the new Tensor, and vice-versa. There is no memory copy!

-- creates a storage with 10 elements
s = torch.Storage(10):fill(1)

-- we want to see it as a 2x5 tensor
x = torch.Tensor(s, 1, torch.LongStorage{2,5})
> x
 1  1  1  1  1
 1  1  1  1  1
[torch.DoubleTensor of dimension 2x5]

x:zero()
> s -- the storage contents have been modified
 0
 0
 0
 0
 0
 0
 0
 0
 0
 0
[torch.DoubleStorage of size 10]

torch.Tensor(storage, [storageOffset, sz1 [, st1 ... [, sz4 [, st4]]]])

Convenience constructor (for the previous constructor) assuming a number of dimensions inferior or equal to 4. szi is the size in the i-th dimension, and sti is the stride in the i-th dimension.

torch.Tensor(table)

The argument is assumed to be a Lua array of numbers. The constructor returns a new Tensor of the size of the table, containing all the table elements. The table might be multi-dimensional.

Example:

> torch.Tensor({{1,2,3,4}, {5,6,7,8}})
 1  2  3  4
 5  6  7  8
[torch.DoubleTensor of dimension 2x4]

A note on function calls

The rest of this guide will present many functions that can be used to manipulate tensors. Most functions have been defined so that they can be called flexibly, either in an object-oriented "method call" style i.e. src:function(...) or a more "functional" style torch.function(src, ...), where src is a tensor. Note that these different invocations may differ in whether they modify the tensor in-place, or create a new tensor. Additionally, some functions can be called in the formdst:function(src, ...) which usually suggests that the result of the operation on the src tensor will be stored in the tensor dst. Further details are given in the individual function definitions, below, but it should be noted that the documentation is currently incomplete in this regard, and readers are encouraged to experiment in an interactive session.

Cloning

[Tensor] clone()

Returns a clone of a tensor. The memory is copied.

i = 0
x = torch.Tensor(5):apply(function(x)
  i = i + 1
  return i
end)
> x
 1
 2
 3
 4
 5
[torch.DoubleTensor of dimension 5]

-- create a clone of x
y = x:clone()
> y
 1
 2
 3
 4
 5
[torch.DoubleTensor of dimension 5]

-- fill up y with 1
y:fill(1)
> y
 1
 1
 1
 1
 1
[torch.DoubleTensor of dimension 5]

-- the contents of x were not changed:
> x
 1
 2
 3
 4
 5
[torch.DoubleTensor of dimension 5]

[Tensor] contiguous

• If the given Tensor contents are contiguous in memory, returns the exact same Tensor (no memory copy).
• Otherwise (not contiguous in memory), returns a clone (memory copy).

x = torch.Tensor(2,3):fill(1)
> x
 1  1  1
 1  1  1
[torch.DoubleTensor of dimension 2x3]

-- x is contiguous, so y points to the same thing
y = x:contiguous():fill(2)
> y
 2  2  2
 2  2  2
[torch.DoubleTensor of dimension 2x3]

-- contents of x have been changed
> x
 2  2  2
 2  2  2
[torch.DoubleTensor of dimension 2x3]

-- x:t() is not contiguous, so z is a clone
z = x:t():contiguous():fill(3.14)
> z
 3.1400  3.1400
 3.1400  3.1400
 3.1400  3.1400
[torch.DoubleTensor of dimension 3x2]

-- contents of x have not been changed
> x
 2  2  2
 2  2  2
[torch.DoubleTensor of dimension 2x3]

[Tensor or string] type(type)

If type is nil, returns a string containing the type name of the given tensor.

= torch.Tensor():type()
torch.DoubleTensor

If type is a string describing a Tensor type, and is equal to the given tensor typename, returns the exact same tensor (//no memory copy//).

x = torch.Tensor(3):fill(3.14)
> x
 3.1400
 3.1400
 3.1400
[torch.DoubleTensor of dimension 3]

y = x:type('torch.DoubleTensor')
> y
 3.1400
 3.1400
 3.1400
[torch.DoubleTensor of dimension 3]

-- zero y contents
y:zero()

-- contents of x have been changed
> x
 0
 0
 0
[torch.DoubleTensor of dimension 3]

If type is a string describing a Tensor type, different from the type name of the given Tensor, returns a new Tensor of the specified type, whose contents corresponds to the contents of the original Tensor, casted to the given type (//memory copy occurs, with possible loss of precision//).

x = torch.Tensor(3):fill(3.14)
> x
 3.1400
 3.1400
 3.1400
[torch.DoubleTensor of dimension 3]

y = x:type('torch.IntTensor')
> y
 3
 3
 3
[torch.IntTensor of dimension 3]

[Tensor] typeAs(tensor)

Convenience method for the type method. Equivalent to

type(tensor:type())

[boolean] isTensor(object)

Returns true iff the provided object is one of the torch.*Tensor types.

> torch.isTensor(torch.randn(3,4))
true

> torch.isTensor(torch.randn(3,4)[1])
true

> torch.isTensor(torch.randn(3,4)[1][2])
false

[Tensor] byte(), char(), short(), int(), long(), float(), double()

Convenience methods for the type method. For e.g.,

x = torch.Tensor(3):fill(3.14)
> x
 3.1400
 3.1400
 3.1400
[torch.DoubleTensor of dimension 3]

-- calling type('torch.IntTensor')
> x:type('torch.IntTensor')
 3
 3
 3
[torch.IntTensor of dimension 3]


-- is equivalent to calling int()
> x:int()
 3
 3
 3
[torch.IntTensor of dimension 3]

Querying the size and structure

[number] nDimension()

Returns the number of dimensions in a Tensor.

x = torch.Tensor(4,5) -- a matrix
> x:nDimension()
2

[number] dim()

Same as nDimension().

[number] size(dim)

Returns the size of the specified dimension dim. Example:

x = torch.Tensor(4,5):zero()
> x
 0 0 0 0 0
 0 0 0 0 0
 0 0 0 0 0
 0 0 0 0 0
[torch.DoubleTensor of dimension 4x5]

> x:size(2) -- gets the number of columns
5

[LongStorage] size()

Returns a LongStorage containing the size of each dimension of the tensor.

x = torch.Tensor(4,5):zero()
> x
 0 0 0 0 0
 0 0 0 0 0
 0 0 0 0 0
 0 0 0 0 0
[torch.DoubleTensor of dimension 4x5]

> x:size()
 4
 5
[torch.LongStorage of size 2]

[LongStorage] #self

Same as size() method.

[number] stride(dim)

Returns the jump necessary to go from one element to the next one in the specified dimension dim. Example:

x = torch.Tensor(4,5):zero()
> x
 0 0 0 0 0
 0 0 0 0 0
 0 0 0 0 0
 0 0 0 0 0
[torch.DoubleTensor of dimension 4x5]

-- elements in a row are contiguous in memory
> x:stride(2)
1

-- to go from one element to the next one in a column
-- we need here to jump the size of the row
> x:stride(1)
5

Note also that in Torch elements in the same row [elements along the last dimension] are contiguous in memory for a matrix [tensor].

[LongStorage] stride()

Returns the jump necessary to go from one element to the next one in each dimension. Example:

x = torch.Tensor(4,5):zero()
> x
 0 0 0 0 0
 0 0 0 0 0
 0 0 0 0 0
 0 0 0 0 0
[torch.DoubleTensor of dimension 4x5]

> x:stride()
 5
 1 -- elements are contiguous in a row [last dimension]
[torch.LongStorage of size 2]

Note also that in Torch elements in the same row [elements along the last dimension] are contiguous in memory for a matrix [tensor].

[Storage] storage()

Returns the Storage used to store all the elements of the Tensor. Basically, a Tensor is a particular way of viewing aStorage.

x = torch.Tensor(4,5)
s = x:storage()
for i=1,s:size() do -- fill up the Storage
  s[i] = i
end

> x -- s is interpreted by x as a 2D matrix
  1   2   3   4   5
  6   7   8   9  10
 11  12  13  14  15
 16  17  18  19  20
[torch.DoubleTensor of dimension 4x5]

[boolean] isContiguous()

Returns true iff the elements of the Tensor are contiguous in memory.

-- normal tensors are contiguous in memory
x = torch.randn(4,5)
> x:isContiguous()
true

-- y now "views" the 3rd column of x
-- the storage of y is the same than x
-- so the memory cannot be contiguous
y = x:select(2, 3)
> y:isContiguous()
false

-- indeed, to jump to one element to
-- the next one, the stride is 5
> y:stride()
 5
[torch.LongStorage of size 1]

[boolean] isSize(storage)

Returns true iff the dimensions of the Tensor match the elements of the storage.

x = torch.Tensor(4,5)
y = torch.LongStorage({4,5})
z = torch.LongStorage({5,4,1})
> x:isSize(y)
true

> x:isSize(z)
false

> x:isSize(x:size())
true

[boolean] isSameSizeAs(tensor)

Returns true iff the dimensions of the Tensor and the argument Tensor are exactly the same.

x = torch.Tensor(4,5)
y = torch.Tensor(4,5)
> x:isSameSizeAs(y)
true

y = torch.Tensor(4,6)
> x:isSameSizeAs(y)
false

[number] nElement()

Returns the number of elements of a tensor.

x = torch.Tensor(4,5)
> x:nElement() -- 4x5 = 20!
20

[number] storageOffset()

Return the first index (starting at 1) used in the tensor's storage.

Querying elements

Elements of a tensor can be retrieved with the [index] operator.

If index is a number, [index] operator is equivalent to a select(1, index). If the tensor has more than one dimension, this operation returns a slice of the tensor that shares the same underlying storage. If the tensor is a 1D tensor, it returns the value at index in this tensor.

If index is a table, the table must contain n numbers, where n is the number of dimensions of the Tensor. It will return the element at the given position.

In the same spirit, index might be a LongStorage, specifying the position (in the Tensor) of the element to be retrieved.

If index is a ByteTensor in which each element is 0 or 1 then it acts as a selection mask used to extract a subset of the original tensor. This is particularly useful with logical operators like torch.le.

Example:

x = torch.Tensor(3,3)
i = 0; x:apply(function() i = i + 1; return i end)
> x
 1  2  3
 4  5  6
 7  8  9
[torch.DoubleTensor of dimension 3x3]

> x[2] -- returns row 2
 4
 5
 6
[torch.DoubleTensor of dimension 3]

> x[2][3] -- returns row 2, column 3
6

> x[{2,3}] -- another way to return row 2, column 3
6

> x[torch.LongStorage{2,3}] -- yet another way to return row 2, column 3
6

> x[torch.le(x,3)] -- torch.le returns a ByteTensor that acts as a mask
 1
 2
 3
[torch.DoubleTensor of dimension 3]

Referencing a tensor to an existing tensor or chunk of memory

A Tensor being a way of viewing a Storage, it is possible to "set" a Tensor such that it views an existing Storage.

Note that if you want to perform a set on an empty Tensor like

y = torch.Storage(10)
x = torch.Tensor()
x:set(y, 1, 10)

you might want in that case to use one of the equivalent constructor.

y = torch.Storage(10)
x = torch.Tensor(y, 1, 10)

[self] set(tensor)

The Tensor is now going to "view" the same storage as the given tensor. As the result, any modification in the elements of the Tensor will have an impact on the elements of the given tensor, and vice-versa. This is an efficient method, as there is no memory copy!

x = torch.Tensor(2,5):fill(3.14)
> x
 3.1400  3.1400  3.1400  3.1400  3.1400
 3.1400  3.1400  3.1400  3.1400  3.1400
[torch.DoubleTensor of dimension 2x5]

y = torch.Tensor():set(x)
> y
 3.1400  3.1400  3.1400  3.1400  3.1400
 3.1400  3.1400  3.1400  3.1400  3.1400
[torch.DoubleTensor of dimension 2x5]

y:zero()
> x -- elements of x are the same than y!
 0 0 0 0 0
 0 0 0 0 0
[torch.DoubleTensor of dimension 2x5]

[boolean] isSetTo(tensor)

Returns true iff the Tensor is set to the argument Tensor. Note: this is only true if the tensors are the same size, have the same strides and share the same storage and offset.

x = torch.Tensor(2,5)
y = torch.Tensor()
> y:isSetTo(x)
 false
> y:set(x)
> y:isSetTo(x)
  true
> y:t():isSetTo(x)
  false -- x and y have different strides

[self] set(storage, [storageOffset, sizes, [strides]])

The Tensor is now going to "view" the given storage, starting at position storageOffset (>=1) with the given dimensionsizes and the optional given strides. As the result, any modification in the elements of the Storage will have a impact on the elements of the Tensor, and vice-versa. This is an efficient method, as there is no memory copy!

If only storage is provided, the whole storage will be viewed as a 1D Tensor.

-- creates a storage with 10 elements
s = torch.Storage(10):fill(1)

-- we want to see it as a 2x5 tensor
sz = torch.LongStorage({2,5})
x = torch.Tensor()
x:set(s, 1, sz)
> x
 1  1  1  1  1
 1  1  1  1  1
[torch.DoubleTensor of dimension 2x5]

x:zero()
> s -- the storage contents have been modified
 0
 0
 0
 0
 0
 0
 0
 0
 0
 0
[torch.DoubleStorage of size 10]

[self] set(storage, [storageOffset, sz1 [, st1 ... [, sz4 [, st4]]]])

This is a "shortcut" for previous method. It works up to 4 dimensions. szi is the size of the i-th dimension of the tensor.sti is the stride in the i-th dimension.

Copying and initializing

[self] copy(tensor)

Replace the elements of the Tensor by copying the elements of the given tensor. The number of elements must match, but the sizes might be different.

x = torch.Tensor(4):fill(1)
y = torch.Tensor(2,2):copy(x)
> x
 1
 1
 1
 1
[torch.DoubleTensor of dimension 4]

> y
 1  1
 1  1
[torch.DoubleTensor of dimension 2x2]

If a different type of tensor is given, then a type conversion occurs, which, of course, might result in loss of precision.

[self] fill(value)

Fill the tensor with the given value.

> torch.DoubleTensor(4):fill(3.14)
 3.1400
 3.1400
 3.1400
 3.1400
[torch.DoubleTensor of dimension 4]

[self] zero()

Fill the tensor with zeros.

> torch.Tensor(4):zero()
 0
 0
 0
 0
[torch.DoubleTensor of dimension 4]

Resizing

When resizing to a larger size, the underlying Storage is resized to fit all the elements of the Tensor.

When resizing to a smaller size, the underlying Storage is not resized.

Important note: the content of a Tensor after resizing is undetermined as strides might have been completely changed. In particular, the elements of the resized tensor are contiguous in memory.

[self] resizeAs(tensor)

Resize the tensor as the given tensor (of the same type).

[self] resize(sizes)

Resize the tensor according to the given LongStorage sizes.

[self] resize(sz1 [,sz2 [,sz3 [,sz4]]]])

Convenience method of the previous method, working for a number of dimensions up to 4.

Extracting sub-tensors

Each of these methods returns a Tensor which is a sub-tensor of the given tensor.

For methods narrow, select and sub the returned tensor shares the same Storage as the original. Hence, any modification in the memory of the sub-tensor will have an impact on the primary tensor, and vice-versa. These methods are very fast, as they do not involve any memory copy.

For all other methods in this section such as index, indexCopy etc., since you cannot extract a shared subtensor (technically), a new tensor is returned. If you make changes in this new tensor, they are not reflected in the original tensor.

[self] narrow(dim, index, size)

Returns a new Tensor which is a narrowed version of the current one: the dimension dim is narrowed from index toindex+size-1.

x = torch.Tensor(5, 6):zero()
> x

0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
[torch.DoubleTensor of dimension 5x6]

y = x:narrow(1, 2, 3) -- narrow dimension 1 from index 2 to index 2+3-1
y:fill(1) -- fill with 1
> y
 1  1  1  1  1  1
 1  1  1  1  1  1
 1  1  1  1  1  1
[torch.DoubleTensor of dimension 3x6]

> x -- memory in x has been modified!
 0  0  0  0  0  0
 1  1  1  1  1  1
 1  1  1  1  1  1
 1  1  1  1  1  1
 0  0  0  0  0  0
[torch.DoubleTensor of dimension 5x6]

[Tensor] sub(dim1s, dim1e ... [, dim4s [, dim4e]])

This method is equivalent to do a series of narrow up to the first 4 dimensions. It returns a new Tensor which is a sub-tensor going from index dimis to dimie in the i-th dimension. Negative values are interpreted index starting from the end: -1 is the last index, -2 is the index before the last index, ...

x = torch.Tensor(5, 6):zero()
> x
 0 0 0 0 0 0
 0 0 0 0 0 0
 0 0 0 0 0 0
 0 0 0 0 0 0
 0 0 0 0 0 0
[torch.DoubleTensor of dimension 5x6]

y = x:sub(2,4):fill(1) -- y is sub-tensor of x:
> y                    -- dimension 1 starts at index 2, ends at index 4
 1  1  1  1  1  1
 1  1  1  1  1  1
 1  1  1  1  1  1
[torch.DoubleTensor of dimension 3x6]

> x                    -- x has been modified!
 0  0  0  0  0  0
 1  1  1  1  1  1
 1  1  1  1  1  1
 1  1  1  1  1  1
 0  0  0  0  0  0
[torch.DoubleTensor of dimension 5x6]

z = x:sub(2,4,3,4):fill(2) -- we now take a new sub-tensor
> z                        -- dimension 1 starts at index 2, ends at index 4
                           -- dimension 2 starts at index 3, ends at index 4
 2  2
 2  2
 2  2
[torch.DoubleTensor of dimension 3x2]

> x                        -- x has been modified
 0  0  0  0  0  0
 1  1  2  2  1  1
 1  1  2  2  1  1
 1  1  2  2  1  1
 0  0  0  0  0  0
[torch.DoubleTensor of dimension 5x6]

> y                        -- y has been modified
 1  1  2  2  1  1
 1  1  2  2  1  1
 1  1  2  2  1  1
[torch.DoubleTensor of dimension 3x6]

> y:sub(-1, -1, 3, 4)      -- negative values = bounds
 2  2
[torch.DoubleTensor of dimension 1x2]

[Tensor] select(dim, index)

Returns a new Tensor which is a tensor slice at the given index in the dimension dim. The returned tensor has one less dimension: the dimension dim is removed. As a result, it is not possible to select() on a 1D tensor.

Note that "selecting" on the first dimension is equivalent to use the [] operator

x = torch.Tensor(5,6):zero()
> x
 0 0 0 0 0 0
 0 0 0 0 0 0
 0 0 0 0 0 0
 0 0 0 0 0 0
 0 0 0 0 0 0
[torch.DoubleTensor of dimension 5x6]

y = x:select(1, 2):fill(2) -- select row 2 and fill up
> y
 2
 2
 2
 2
 2
 2
[torch.DoubleTensor of dimension 6]

> x
 0  0  0  0  0  0
 2  2  2  2  2  2
 0  0  0  0  0  0
 0  0  0  0  0  0
 0  0  0  0  0  0
[torch.DoubleTensor of dimension 5x6]

z = x:select(2,5):fill(5) -- select column 5 and fill up
> z
 5
 5
 5
 5
 5
[torch.DoubleTensor of dimension 5]

> x
 0  0  0  0  5  0
 2  2  2  2  5  2
 0  0  0  0  5  0
 0  0  0  0  5  0
 0  0  0  0  5  0
[torch.DoubleTensor of dimension 5x6]

[Tensor] [{ dim1,dim2,... }] or [{ {dim1s,dim1e}, {dim2s,dim2e} }]

The indexing operator [] can be used to combine narrow/sub and select in a concise and efficient way. It can also be used to copy, and fill (sub) tensors.

This operator also works with an input mask made of a ByteTensor with 0 and 1 elements, e.g with a logical operator.

x = torch.Tensor(5, 6):zero()
> x
 0 0 0 0 0 0
 0 0 0 0 0 0
 0 0 0 0 0 0
 0 0 0 0 0 0
 0 0 0 0 0 0
[torch.DoubleTensor of dimension 5x6]

x[{ 1,3 }] = 1 -- sets element at (i=1,j=3) to 1
> x
 0  0  1  0  0  0
 0  0  0  0  0  0
 0  0  0  0  0  0
 0  0  0  0  0  0
 0  0  0  0  0  0
[torch.DoubleTensor of dimension 5x6]

x[{ 2,{2,4} }] = 2  -- sets a slice of 3 elements to 2
> x
 0  0  1  0  0  0
 0  2  2  2  0  0
 0  0  0  0  0  0
 0  0  0  0  0  0
 0  0  0  0  0  0
[torch.DoubleTensor of dimension 5x6]

x[{ {},4 }] = -1 -- sets the full 4th column to -1
> x
 0  0  1 -1  0  0
 0  2  2 -1  0  0
 0  0  0 -1  0  0
 0  0  0 -1  0  0
 0  0  0 -1  0  0
[torch.DoubleTensor of dimension 5x6]

x[{ {},2 }] = torch.range(1,5) -- copy a 1D tensor to a slice of x
> x

 0  1  1 -1  0  0
 0  2  2 -1  0  0
 0  3  0 -1  0  0
 0  4  0 -1  0  0
 0  5  0 -1  0  0
[torch.DoubleTensor of dimension 5x6]

x[torch.lt(x,0)] = -2 -- sets all negative elements to -2 via a mask
> x

 0  1  1 -2  0  0
 0  2  2 -2  0  0
 0  3  0 -2  0  0
 0  4  0 -2  0  0
 0  5  0 -2  0  0
[torch.DoubleTensor of dimension 5x6]

[Tensor] index(dim, index)

Returns a new Tensor which indexes the original Tensor along dimension dim using the entries in torch.LongTensorindex. The returned Tensor has the same number of dimensions as the original Tensor. The returned Tensor does notuse the same storage as the original Tensor -- see below for storing the result in an existing Tensor.

x = torch.rand(5,5)
> x
 0.8020  0.7246  0.1204  0.3419  0.4385
 0.0369  0.4158  0.0985  0.3024  0.8186
 0.2746  0.9362  0.2546  0.8586  0.6674
 0.7473  0.9028  0.1046  0.9085  0.6622
 0.1412  0.6784  0.1624  0.8113  0.3949
[torch.DoubleTensor of dimension 5x5]

y = x:index(1,torch.LongTensor{3,1})
> y
 0.2746  0.9362  0.2546  0.8586  0.6674
 0.8020  0.7246  0.1204  0.3419  0.4385
[torch.DoubleTensor of dimension 2x5]

y:fill(1)
> y
 1  1  1  1  1
 1  1  1  1  1
[torch.DoubleTensor of dimension 2x5]

> x
 0.8020  0.7246  0.1204  0.3419  0.4385
 0.0369  0.4158  0.0985  0.3024  0.8186
 0.2746  0.9362  0.2546  0.8586  0.6674
 0.7473  0.9028  0.1046  0.9085  0.6622
 0.1412  0.6784  0.1624  0.8113  0.3949
[torch.DoubleTensor of dimension 5x5]

Note the explicit index function is different than the indexing operator []. The indexing operator [] is a syntactic shortcut for a series of select and narrow operations, therefore it always returns a new view on the original tensor that shares the same storage. However, the explicit index function can not use the same storage.

It is possible to store the result into an existing Tensor with result:index(source, ...):

x = torch.rand(5,5)
> x
 0.8020  0.7246  0.1204  0.3419  0.4385
 0.0369  0.4158  0.0985  0.3024  0.8186
 0.2746  0.9362  0.2546  0.8586  0.6674
 0.7473  0.9028  0.1046  0.9085  0.6622
 0.1412  0.6784  0.1624  0.8113  0.3949
[torch.DoubleTensor of dimension 5x5]

y = torch.Tensor()
y:index(x,1,torch.LongTensor{3,1})
> y
 0.2746  0.9362  0.2546  0.8586  0.6674
 0.8020  0.7246  0.1204  0.3419  0.4385
[torch.DoubleTensor of dimension 2x5]

[Tensor] indexCopy(dim, index, tensor)

Copies the elements of tensor into the original tensor by selecting the indices in the order given in index. The shape oftensor must exactly match the elements indexed or an error will be thrown.

> x
 0.8020  0.7246  0.1204  0.3419  0.4385
 0.0369  0.4158  0.0985  0.3024  0.8186
 0.2746  0.9362  0.2546  0.8586  0.6674
 0.7473  0.9028  0.1046  0.9085  0.6622
 0.1412  0.6784  0.1624  0.8113  0.3949
[torch.DoubleTensor of dimension 5x5]

z=torch.Tensor(5,2)
z:select(2,1):fill(-1)
z:select(2,2):fill(-2)
> z
-1 -2
-1 -2
-1 -2
-1 -2
-1 -2
[torch.DoubleTensor of dimension 5x2]

x:indexCopy(2,torch.LongTensor{5,1},z)
> x
-2.0000  0.7246  0.1204  0.3419 -1.0000
-2.0000  0.4158  0.0985  0.3024 -1.0000
-2.0000  0.9362  0.2546  0.8586 -1.0000
-2.0000  0.9028  0.1046  0.9085 -1.0000
-2.0000  0.6784  0.1624  0.8113 -1.0000
[torch.DoubleTensor of dimension 5x5]

[Tensor] indexAdd(dim, index, tensor)

Accumulate the elements of tensor into the original tensor by adding to the indices in the order given in index. The shape of tensor must exactly match the elements indexed or an error will be thrown.

Example 1

> x
-2.1742  0.5688 -1.0201  0.1383  1.0504
 0.0970  0.2169  0.1324  0.9553 -1.9518
-0.7607  0.8947  0.1658 -0.2181 -2.1237
-1.4099  0.2342  0.4549  0.6316 -0.2608
 0.0349  0.4713  0.0050  0.1677  0.2103
[torch.DoubleTensor of size 5x5]

z=torch.Tensor(5, 2)
z:select(2,1):fill(-1)
z:select(2,2):fill(-2)
> z
-1 -2
-1 -2
-1 -2
-1 -2
-1 -2
[torch.DoubleTensor of dimension 5x2]

> x:indexAdd(2,torch.LongTensor{5,1},z)
> x
-4.1742  0.5688 -1.0201  0.1383  0.0504
-1.9030  0.2169  0.1324  0.9553 -2.9518
-2.7607  0.8947  0.1658 -0.2181 -3.1237
-3.4099  0.2342  0.4549  0.6316 -1.2608
-1.9651  0.4713  0.0050  0.1677 -0.7897
[torch.DoubleTensor of size 5x5]

Example 2

> a = torch.range(1, 5)
> a
 1
 2
 3
 4
 5
[torch.DoubleTensor of size 5]

> a:indexAdd(1, torch.LongTensor{1, 1, 3, 3}, torch.range(1, 4))
> a
  4
  2
 10
  4
  5
[torch.DoubleTensor of size 5]

[Tensor] indexFill(dim, index, val)

Fills the elements of the original Tensor with value val by selecting the indices in the order given in index.

x=torch.rand(5,5)
> x
 0.8414  0.4121  0.3934  0.5600  0.5403
 0.3029  0.2040  0.7893  0.6079  0.6334
 0.3743  0.1389  0.1573  0.1357  0.8460
 0.2838  0.9925  0.0076  0.7220  0.5185
 0.8739  0.6887  0.4271  0.0385  0.9116
[torch.DoubleTensor of dimension 5x5]

x:indexFill(2,torch.LongTensor{4,2},-10)
> x
  0.8414 -10.0000   0.3934 -10.0000   0.5403
  0.3029 -10.0000   0.7893 -10.0000   0.6334
  0.3743 -10.0000   0.1573 -10.0000   0.8460
  0.2838 -10.0000   0.0076 -10.0000   0.5185
  0.8739 -10.0000   0.4271 -10.0000   0.9116
[torch.DoubleTensor of dimension 5x5]

[Tensor] gather(dim, index)

Creates a new Tensor from the original tensor by gathering a number of values from each "row", where the rows are along the dimension dim. The values in a LongTensor, passed as index, specify which values to take from each row. Specifically, the resulting Tensor, which will have the same size as the index tensor, is given by

-- dim = 1
result[i][j][k]... = src[index[i][j][k]...][j][k]...

-- dim = 2
result[i][j][k]... = src[i][index[i][j][k]...][k]...

-- etc.

where src is the original Tensor.

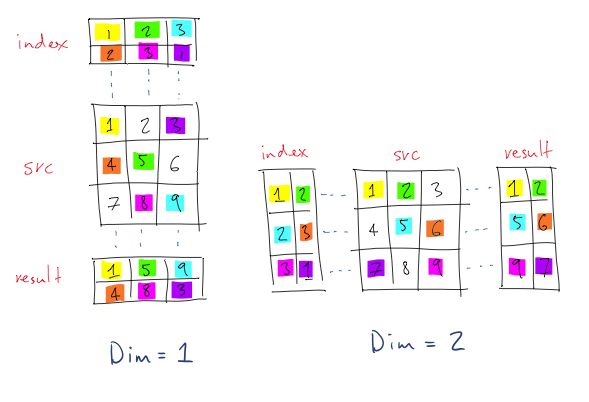
The same number of values are selected from each row, and the same value cannot be selected from a row more than once. The values in the index tensor must not be larger than the length of the row, that is they must be between 1 andsrc:size(dim) inclusive. It can be somewhat confusing to ensure that the index tensor has the correct shape. Viewed pictorially:

Numerically, to give an example, if src has size n x m x p x q, we are gathering along dim = 3, and we wish to gatherk elements from each row (where k <= p) then index must have size n x m x k x q.

It is possible to store the result into an existing Tensor with result:gather(src, ...).

x = torch.rand(5, 5)
> x
 0.7259  0.5291  0.4559  0.4367  0.4133
 0.0513  0.4404  0.4741  0.0658  0.0653
 0.3393  0.1735  0.6439  0.1011  0.7923
 0.7606  0.5025  0.5706  0.7193  0.1572
 0.1720  0.3546  0.8354  0.8339  0.3025
[torch.DoubleTensor of size 5x5]

y = x:gather(1, torch.LongTensor{{1, 2, 3, 4, 5}, {2, 3, 4, 5, 1}})
> y
 0.7259  0.4404  0.6439  0.7193  0.3025
 0.0513  0.1735  0.5706  0.8339  0.4133
[torch.DoubleTensor of size 2x5]

z = x:gather(2, torch.LongTensor{{1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 1}})
> z
 0.7259  0.5291
 0.4404  0.4741
 0.6439  0.1011
 0.7193  0.1572
 0.3025  0.1720
[torch.DoubleTensor of size 5x2]

[Tensor] scatter(dim, index, src|val)

Writes all values from tensor src or the scalar val into self at the specified indices. The indices are specified with respect to the given dimension, dim, in the manner described in gather. Note that, as for gather, the values of index must be between 1 and self:size(dim) inclusive and all values in a row along the specified dimension must be unique.

x = torch.rand(2, 5)
> x
 0.3227  0.4294  0.8476  0.9414  0.1159
 0.7338  0.5185  0.2947  0.0578  0.1273
[torch.DoubleTensor of size 2x5]

y = torch.zeros(3, 5):scatter(1, torch.LongTensor{{1, 2, 3, 1, 1}, {3, 1, 1, 2, 3}}, x)
> y
 0.3227  0.5185  0.2947  0.9414  0.1159
 0.0000  0.4294  0.0000  0.0578  0.0000
 0.7338  0.0000  0.8476  0.0000  0.1273
[torch.DoubleTensor of size 3x5]

z = torch.zeros(2, 4):scatter(2, torch.LongTensor{{3}, {4}}, 1.23)
> z
 0.0000  0.0000  1.2300  0.0000
 0.0000  0.0000  0.0000  1.2300
[torch.DoubleTensor of size 2x4]

[Tensor] maskedSelect(mask)

Returns a new Tensor which contains all elements aligned to a 1 in the corresponding mask. This mask is atorch.ByteTensor of zeros and ones. The mask and Tensor must have the same number of elements. The resulting Tensor will be a 1D tensor of the same type as Tensor having size mask:sum().

x = torch.range(1,12):double():resize(3,4)
> x
  1   2   3   4
  5   6   7   8
  9  10  11  12
[torch.DoubleTensor of dimension 3x4]

mask = torch.ByteTensor(2,6):bernoulli()
> mask
 1  0  1  0  0  0
 1  1  0  0  0  1
[torch.ByteTensor of dimension 2x6]

y = x:maskedSelect(mask)
> y
  1
  3
  7
  8
 12
[torch.DoubleTensor of dimension 5]

z = torch.DoubleTensor()
z:maskedSelect(x, mask)
> z
  1
  3
  7
  8
 12

Note how the dimensions of the above x, mask and y do not match. Also note how an existing tensor z can be used to store the results.

[Tensor] maskedCopy(mask, tensor)

Copies the elements of tensor into mask locations of itself. The masked elements are those elements having a corresponding 1 in the mask Tensor. This mask is a torch.ByteTensor of zeros and ones. The destination Tensor and the mask Tensor should have the same number of elements. The source tensor should have at least as many elements as the number of 1s in the mask.

x = torch.Tensor({0, 0, 0, 0})
mask = torch.ByteTensor({0, 1, 0, 1})
y = torch.Tensor({10, 20})
x:maskedCopy(mask,y)
print(x)

  0
 10
  0
 20
[torch.DoubleTensor of size 4]

x = torch.range(1,4):double():resize(2,2)
> x
 1  2
 3  4
[torch.DoubleTensor of dimension 2x4]

mask = torch.ByteTensor(1,8):bernoulli()
> mask
 0  0  1  1  1  0  1  0
[torch.ByteTensor of dimension 1x8]

y = torch.DoubleTensor(2,4):fill(-1)
> y
-1 -1 -1 -1
-1 -1 -1 -1
[torch.DoubleTensor of dimension 2x4]

y:maskedCopy(mask, x)
> y
 -1 -1  1  2
  3 -1  4 -1
[torch.DoubleTensor of dimension 2x4]

Note how the dimensions of the above x, mask and `y' do not match, but the number of elements do.

[Tensor] maskedFill(mask, val)

Fills the masked elements of itself with value val. The masked elements are those elements having a corresponding 1 in the mask Tensor. This mask is a torch.ByteTensor of zeros and ones. The mask and Tensor must have the same number of elements.

x = torch.range(1,4):double():resize(1,4)
> x
 1  2  3  4
[torch.DoubleTensor of dimension 1x4]

mask = torch.ByteTensor(2,2):bernoulli()
> mask
 0  0
 1  1
[torch.ByteTensor of dimension 2x2]

x:maskedFill(mask, -1)
> x
 1  2 -1 -1
[torch.DoubleTensor of dimension 1x4]

Note how the dimensions of the above x and mask do not match, but the number of elements do.

Search

Each of these methods returns a LongTensor corresponding to the indices of the given search operation.

[LongTensor] nonzero(tensor)

Finds and returns a LongTensor corresponding to the subscript indices of all non-zero elements in tensor.

Note that torch uses the first argument on dispatch to determine the return type. Since the first argument is anytorch.TensorType, but the return type is always torch.LongTensor, the function calltorch.nonzero(torch.LongTensor(), tensor) does not work. However, tensor.nonzero(torch.LongTensor(), tensor) does work.

> x = torch.rand(4, 4):mul(3):floor():int()
> x
 2  0  2  0
 0  0  1  2
 0  2  2  1
 2  1  2  2
[torch.IntTensor of dimension 4x4]

> torch.nonzero(x)
 1  1
 1  3
 2  3
 2  4
 3  2
 3  3
 3  4
 4  1
 4  2
 4  3
 4  4
[torch.LongTensor of dimension 11x2]

> x:nonzero()
 1  1
 1  3
 2  3
 2  4
 3  2
 3  3
 3  4
 4  1
 4  2
 4  3
 4  4
[torch.LongTensor of dimension 11x2]

> indices = torch.LongTensor()
> x.nonzero(indices, x)
 1  1
 1  3
 2  3
 2  4
 3  2
 3  3
 3  4
 4  1
 4  2
 4  3
 4  4
[torch.LongTensor of dimension 11x2]

> x:eq(1):nonzero()
 2  3
 3  4
 4  2
[torch.LongTensor of dimension 3x2]

Expanding/Replicating/Squeezing Tensors

These methods returns a Tensor which is created by replications of the original tensor.

[result] expand([result,] sizes)

sizes can either be a torch.LongStorage or numbers. Expanding a tensor does not allocate new memory, but only creates a new view on the existing tensor where singleton dimensions can be expanded to multiple ones by setting thestride to 0. Any dimension that has size 1 can be expanded to arbitrary value without any new memory allocation. Attempting to expand along a dimension that does not have size 1 will result in an error.

x = torch.rand(10,1)
> x
 0.3837
 0.5966
 0.0763
 0.1896
 0.4958
 0.6841
 0.4038
 0.4068
 0.1502
 0.2239
[torch.DoubleTensor of dimension 10x1]

y = torch.expand(x,10,2)
> y
 0.3837  0.3837
 0.5966  0.5966
 0.0763  0.0763
 0.1896  0.1896
 0.4958  0.4958
 0.6841  0.6841
 0.4038  0.4038
 0.4068  0.4068
 0.1502  0.1502
 0.2239  0.2239
[torch.DoubleTensor of dimension 10x2]

y:fill(1)
> y
 1  1
 1  1
 1  1
 1  1
 1  1
 1  1
 1  1
 1  1
 1  1
 1  1
[torch.DoubleTensor of dimension 10x2]

> x
 1
 1
 1
 1
 1
 1
 1
 1
 1
 1
[torch.DoubleTensor of dimension 10x1]

i=0; y:apply(function() i=i+1;return i end)
> y
  2   2
  4   4
  6   6
  8   8
 10  10
 12  12
 14  14
 16  16
 18  18
 20  20
[torch.DoubleTensor of dimension 10x2]

> x
  2
  4
  6
  8
 10
 12
 14
 16
 18
 20
[torch.DoubleTensor of dimension 10x1]

[result] expandAs([result,] tensor)

This is equivalent to self:expand(tensor:size())

[Tensor] repeatTensor([result,] sizes)

sizes can either be a torch.LongStorage or numbers. Repeating a tensor allocates new memory, unless result is provided, in which case its memory is resized. sizes specify the number of times the tensor is repeated in each dimension.

x = torch.rand(5)
> x
 0.7160
 0.6514
 0.0704
 0.7856
 0.7452
[torch.DoubleTensor of dimension 5]

> torch.repeatTensor(x,3,2)
 0.7160  0.6514  0.0704  0.7856  0.7452  0.7160  0.6514  0.0704  0.7856  0.7452
 0.7160  0.6514  0.0704  0.7856  0.7452  0.7160  0.6514  0.0704  0.7856  0.7452
 0.7160  0.6514  0.0704  0.7856  0.7452  0.7160  0.6514  0.0704  0.7856  0.7452
[torch.DoubleTensor of dimension 3x10]

> torch.repeatTensor(x,3,2,1)
(1,.,.) =
  0.7160  0.6514  0.0704  0.7856  0.7452
  0.7160  0.6514  0.0704  0.7856  0.7452

(2,.,.) =
  0.7160  0.6514  0.0704  0.7856  0.7452
  0.7160  0.6514  0.0704  0.7856  0.7452

(3,.,.) =
  0.7160  0.6514  0.0704  0.7856  0.7452
  0.7160  0.6514  0.0704  0.7856  0.7452
[torch.DoubleTensor of dimension 3x2x5]

[Tensor] squeeze([dim])

Removes all singleton dimensions of the tensor. If dim is given, squeezes only that particular dimension of the tensor.

x=torch.rand(2,1,2,1,2)
> x
(1,1,1,.,.) =
  0.6020  0.8897

(2,1,1,.,.) =
  0.4713  0.2645

(1,1,2,.,.) =
  0.4441  0.9792

(2,1,2,.,.) =
  0.5467  0.8648
[torch.DoubleTensor of dimension 2x1x2x1x2]

> torch.squeeze(x)
(1,.,.) =
  0.6020  0.8897
  0.4441  0.9792

(2,.,.) =
  0.4713  0.2645
  0.5467  0.8648
[torch.DoubleTensor of dimension 2x2x2]

> torch.squeeze(x,2)
(1,1,.,.) =
  0.6020  0.8897

(2,1,.,.) =
  0.4713  0.2645

(1,2,.,.) =
  0.4441  0.9792

(2,2,.,.) =
  0.5467  0.8648
[torch.DoubleTensor of dimension 2x2x1x2]

Manipulating the tensor view

Each of these methods returns a Tensor which is another way of viewing the Storage of the given tensor. Hence, any modification in the memory of the sub-tensor will have an impact on the primary tensor, and vice-versa.

These methods are very fast, because they do not involve any memory copy.

[result] view([result,] tensor, sizes)

Creates a view with different dimensions of the storage associated with tensor. If result is not passed, then a new tensor is returned, otherwise its storage is made to point to storage of tensor.

sizes can either be a torch.LongStorage or numbers. If one of the dimensions is -1, the size of that dimension is inferred from the rest of the elements.

x = torch.zeros(4)
> x:view(2,2)
 0 0
 0 0
[torch.DoubleTensor of dimension 2x2]

> x:view(2,-1)
 0 0
 0 0
[torch.DoubleTensor of dimension 2x2]

> x:view(torch.LongStorage{2,2})
 0 0
 0 0
[torch.DoubleTensor of dimension 2x2]

> x
 0
 0
 0
 0
[torch.DoubleTensor of dimension 4]

[result] viewAs([result,] tensor, template)

Creates a view with the same dimensions as template of the storage associated with tensor. If result is not passed, then a new tensor is returned, otherwise its storage is made to point to storage of tensor.

x = torch.zeros(4)
y = torch.Tensor(2,2)
> x:viewAs(y)
 0 0
 0 0
[torch.DoubleTensor of dimension 2x2]

[Tensor] transpose(dim1, dim2)

Returns a tensor where dimensions dim1 and dim2 have been swapped. For 2D tensors, the convenience method of t() is available.

x = torch.Tensor(3,4):zero()
x:select(2,3):fill(7) -- fill column 3 with 7
> x
 0  0  7  0
 0  0  7  0
 0  0  7  0
[torch.DoubleTensor of dimension 3x4]

y = x:transpose(1,2) -- swap dimension 1 and 2
> y
 0  0  0
 0  0  0
 7  7  7
 0  0  0
[torch.DoubleTensor of dimension 4x3]

y:select(2, 3):fill(8) -- fill column 3 with 8
> y
 0  0  8
 0  0  8
 7  7  8
 0  0  8
[torch.DoubleTensor of dimension 4x3]

> x -- contents of x have changed as well
 0  0  7  0
 0  0  7  0
 8  8  8  8
[torch.DoubleTensor of dimension 3x4]

[Tensor] t()

Convenience method of transpose() for 2D tensors. The given tensor must be 2 dimensional. Swap dimensions 1 and 2.

x = torch.Tensor(3,4):zero()
x:select(2,3):fill(7)
y = x:t()
> y
 0  0  0
 0  0  0
 7  7  7
 0  0  0
[torch.DoubleTensor of dimension 4x3]

> x
 0  0  7  0
 0  0  7  0
 0  0  7  0
[torch.DoubleTensor of dimension 3x4]

[Tensor] permute(dim1, dim2, ..., dimn)

Generalizes the function transpose() and can be used as a convenience method replacing a sequence of transpose() calls. Returns a tensor where the dimensions were permuted according to the permutation given by (dim1, dim2, ... , dimn). The permutation must be specified fully, i.e. there must be as many parameters as the tensor has dimensions.

x = torch.Tensor(3,4,2,5)
> x:size()
 3
 4
 2
 5
[torch.LongStorage of size 4]

y = x:permute(2,3,1,4) -- equivalent to y = x:transpose(1,3):transpose(1,2)
> y:size()
 4
 2
 3
 5
[torch.LongStorage of size 4]

[Tensor] unfold(dim, size, step)

Returns a tensor which contains all slices of size size in the dimension dim. Step between two slices is given by step.

If sizedim is the original size of dimension dim, the size of dimension dim in the returned tensor will be (sizedim - size) / step + 1

An additional dimension of size size is appended in the returned tensor.

x = torch.Tensor(7)
for i=1,7 do x[i] = i end
> x
 1
 2
 3
 4
 5
 6
 7
[torch.DoubleTensor of dimension 7]

> x:unfold(1, 2, 1)
 1  2
 2  3
 3  4
 4  5
 5  6
 6  7
[torch.DoubleTensor of dimension 6x2]

> x:unfold(1, 2, 2)
 1  2
 3  4
 5  6
[torch.DoubleTensor of dimension 3x2]

Applying a function to a tensor

These functions apply a function to each element of the tensor on which called the method (self). These methods are much faster than using a for loop in Lua. The results is stored in self (if the function returns something).

[self] apply(function)

Apply the given function to all elements of self.

The function takes a number (the current element of the tensor) and might return a number, in which case it will be stored in self.

Examples:

i = 0
z = torch.Tensor(3,3)
z:apply(function(x)
  i = i + 1
  return i
end) -- fill up the tensor
> z
 1  2  3
 4  5  6
 7  8  9
[torch.DoubleTensor of dimension 3x3]

z:apply(math.sin) -- apply the sin function
> z
 0.8415  0.9093  0.1411
-0.7568 -0.9589 -0.2794
 0.6570  0.9894  0.4121
[torch.DoubleTensor of dimension 3x3]

sum = 0
z:apply(function(x)
  sum = sum + x
end) -- compute the sum of the elements
> sum
1.9552094821074

> z:sum() -- it is indeed correct!
1.9552094821074

[self] map(tensor, function(xs, xt))

Apply the given function to all elements of self and tensor. The number of elements of both tensors must match, but sizes do not matter.

The function takes two numbers (the current element of self and tensor) and might return a number, in which case it will be stored in self.

Example:

x = torch.Tensor(3,3)
y = torch.Tensor(9)
i = 0
x:apply(function() i = i + 1; return i end) -- fill-up x
i = 0
y:apply(function() i = i + 1; return i end) -- fill-up y
> x
 1  2  3
 4  5  6
 7  8  9
[torch.DoubleTensor of dimension 3x3]

> y
 1
 2
 3
 4
 5
 6
 7
 8
 9
[torch.DoubleTensor of dimension 9]

x:map(y, function(xx, yy) return xx*yy end) -- element-wise multiplication
> x
  1   4   9
 16  25  36
 49  64  81
[torch.DoubleTensor of dimension 3x3]

[self] map2(tensor1, tensor2, function(x, xt1, xt2))

Apply the given function to all elements of self, tensor1 and tensor2. The number of elements of all tensors must match, but sizes do not matter.

The function takes three numbers (the current element of self, tensor1 and tensor2) and might return a number, in which case it will be stored in self.

Example:

x = torch.Tensor(3,3)
y = torch.Tensor(9)
z = torch.Tensor(3,3)

i = 0; x:apply(function() i = i + 1; return math.cos(i)*math.cos(i) end)
i = 0; y:apply(function() i = i + 1; return i end)
i = 0; z:apply(function() i = i + 1; return i end)

> x
 0.2919  0.1732  0.9801
 0.4272  0.0805  0.9219
 0.5684  0.0212  0.8302
[torch.DoubleTensor of dimension 3x3]

> y
 1
 2
 3
 4
 5
 6
 7
 8
 9
[torch.DoubleTensor of dimension 9]

> z
 1  2  3
 4  5  6
 7  8  9
[torch.DoubleTensor of dimension 3x3]

x:map2(y, z, function(xx, yy, zz) return xx+yy*zz end)
> x
  1.2919   4.1732   9.9801
 16.4272  25.0805  36.9219
 49.5684  64.0212  81.8302
[torch.DoubleTensor of dimension 3x3]

Dividing a tensor into a table of tensors

These functions divide a Tensor into a table of Tensors.

[result] split([result,] tensor, size, [dim])

Splits Tensor tensor along dimension dim into a result table of Tensors of size size (a number) or less (in the case of the last Tensor). The sizes of the non-dim dimensions remain unchanged. Internally, a series of narrows are performed along dimensions dim. Argument dim defaults to 1.

If result is not passed, then a new table is returned, otherwise it is emptied and reused.

Example:

x = torch.randn(3,4,5)

> x:split(2,1)
{
  1 : DoubleTensor - size: 2x4x5
  2 : DoubleTensor - size: 1x4x5
}

> x:split(3,2)
{
  1 : DoubleTensor - size: 3x3x5
  2 : DoubleTensor - size: 3x1x5
}

> x:split(2,3)
{
  1 : DoubleTensor - size: 3x4x2
  2 : DoubleTensor - size: 3x4x2
  3 : DoubleTensor - size: 3x4x1
}

[result] chunk([result,] tensor, n, [dim])

Splits Tensor tensor into n chunks of approximately equal size along dimensions dim and returns these as a resulttable of Tensors. Argument dim defaults to 1.

This function uses split internally:

torch.split(result, tensor, math.ceil(tensor:size(dim)/n), dim)

Example:

x = torch.randn(3,4,5)

> x:chunk(2,1)
{
  1 : DoubleTensor - size: 2x4x5
  2 : DoubleTensor - size: 1x4x5
}

> x:chunk(2,2)
{
  1 : DoubleTensor - size: 3x2x5
  2 : DoubleTensor - size: 3x2x5
}

> x:chunk(2,3)
{
  1 : DoubleTensor - size: 3x4x3
  2 : DoubleTensor - size: 3x4x2
}

LuaJIT FFI access

These functions expose Torch's Tensor and Storage data structures, through LuaJIT FFI. This allows extremely fast access to Tensors and Storages, all from Lua.

[result] data(tensor, [asnumber])

Returns a LuaJIT FFI pointer to the raw data of the tensor. If asnumber is true, then returns the pointer as a intptr_tcdata that you can transform to a plain lua number with tonumber().

Accessing the raw data of a Tensor like this is extremely efficient, in fact, it's almost as fast as C in lots of cases.

Example:

t = torch.randn(3,2)
> t
 0.8008 -0.6103
 0.6473 -0.1870
-0.0023 -0.4902
[torch.DoubleTensor of dimension 3x2]

t_data = torch.data(t)
for i = 0,t:nElement()-1 do t_data[i] = 0 end
> t
 0 0
 0 0
 0 0
[torch.DoubleTensor of dimension 3x2]

WARNING: bear in mind that accessing the raw data like this is dangerous, and should only be done on contiguous tensors (if a tensor is not contiguous, then you have to use its size and stride information). Making sure a tensor is contiguous is easy:

t = torch.randn(3,2)
t_noncontiguous = t:transpose(1,2)

-- it would be unsafe to work with torch.data(t_noncontiguous)
t_transposed_and_contiguous = t_noncontiguous:contiguous()

-- it is now safe to work with the raw pointer
data = torch.data(t_transposed_and_contiguous)

Last, the pointer can be returned as a plain intptr_t cdata. This can be useful to share pointers between threads (warning: this is dangerous, as the second tensor doesn't increment the reference counter on the storage. If the first tensor gets freed, then the data of the second tensor becomes a dangling pointer):

t = torch.randn(10)
p = tonumber(torch.data(t,true))
s = torch.Storage(10, p)
tt = torch.Tensor(s)
-- tt and t are a view on the same data.

[result] cdata(tensor, [asnumber])

Returns a LuaJIT FFI pointer to the C structure of the tensor. Use this with caution, and look at FFI.lua for the members of the tensor

Reference counting

Tensors are reference-counted. It means that each time an object (C or the Lua state) need to keep a reference over a tensor, the corresponding tensor reference counter will be increased. The reference counter is decreased when the object does not need the tensor anymore.

These methods should be used with extreme care. In general, they should never be called, except if you know what you are doing, as the handling of references is done automatically. They can be useful in threaded environments. Note that these methods are atomic operations.

retain()

Increment the reference counter of the tensor.

free()

Decrement the reference counter of the tensor. Free the tensor if the counter is at 0.