排序算法—基数排序
基数排序
基数排序(Radix Sort)属于分配排序的一种,由赫尔曼·何乐礼发明提出。多数的排序算法都是基于关键字之间的比较,判断大小,然后再进行调整。分配排序则不同,它无需进行关键字的比较,而是利用关键字的结构,通过“分配”和“收集”的办法来实现排序。分配排序可分为箱排序和基数排序两类。
题目描述
给出一组数据,根据由小到大顺序输出。
输入要求:
输入一个整数n(数据长度)
输入n个数据
输出要求:
输出由小到大排序后的数据
样例输入:
样例1
10
37 28 46 12 55 0 99 84 63 71
样例2
4
53 47 53 47 00000
样例输出:
样例1
0 12 28 37 46 55 63 71 84 99
样例2
47 47 53 53 00000
基本思想
基数排序的思想建立在箱排序基础之上,所以先来聊聊箱排序。
箱排序(Bin Sort)也称为桶排序(Bucket Sort),其排序思想是:准备若干个箱子,然后依次扫描待排序记录,将关键字等于k的记录装入第k个箱子中(分配),接着,按序号依次将非空箱子里元素输出(收集)。
例如,现有待排序记录 5 7 9 3 2 1 4 0 8 6,待排序记录取值范围是0 ~ 9,所以应准备序号为0 ~ 9的10个箱子。

将关键字放在对应序号的箱子里,然后按序号输出非空箱子里的关键字。
整个过程大致分为三步:①把冰箱门打开②把大象放进去③把冰箱门关上 皮一下ヽ( ̄▽ ̄)ノ ①准备箱子②分箱③装箱。需注意的是:准备箱子的个数取决于待排序记录的取值范围,而不是记录的个数。
若对取值范围0 ~ 99的记录排序,即准备100个箱子,序号为0 ~ 999;若对取值范围0 ~ 999的记录排序,即准备1000个箱子,序号为0 ~ 999。由此,箱排序的缺点也暴露出来了,例如,我们要对 37 28 46 12 55 0 99 84 63 71 这10个记录排序,其取值范围0 ~ 99,需准备100个箱子,然后将记录放入对应序号的箱子中。这时就发现,准备了100个箱子,10个记录分好箱后,有90个箱子都是空的,没有利用上,浪费了空间。
为了更好的解决箱排序的缺点,我们可以仔细分析关键字的结构,就可以找到改进的方法。引入一个例子,扑克牌是很常见的东西,一张扑克牌主要由两个属性组成,即点数和花色。
那我们要将一副打乱的扑克牌排好,首先可以按花色分成♠ ♥ ♣ ♦四组,然后每组内再按A 2 3 4 5 6 7 8 9 10 J Q K排序,这样我们即可将一副扑克牌按序排好。
那对于单纯的数字该如何做?数字的取值范围是无穷大的,但每一个数字都是由个位、十位、百位…组合起来的,并且每一位的数字取值范围都是0 ~ 9。基数排序即是利用这种思路对箱排序进行的改进和推广,先将关键字按个位进行箱排序,然后在对十位进行箱排序…最大数字是几位数就进行几趟排序,即可得到最终结果。
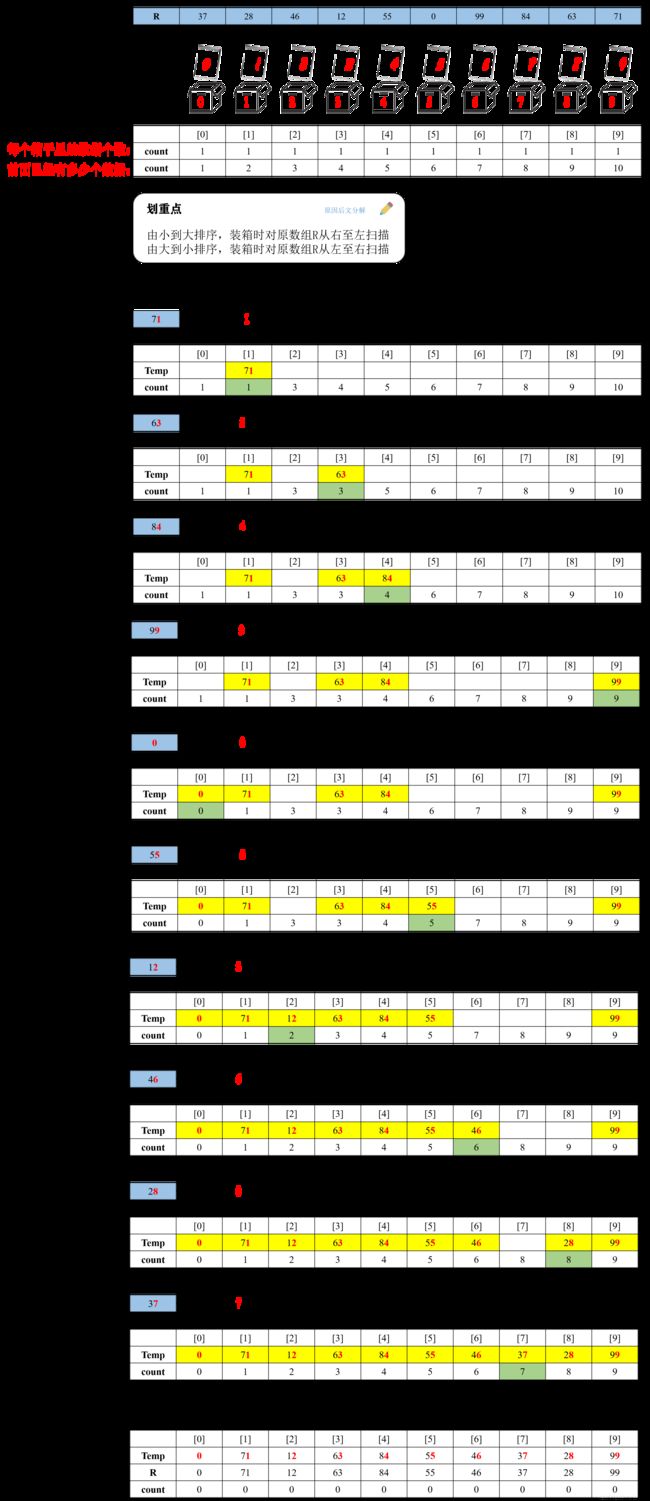
假设待排序的数据都存放在数组R[n]中,准备临时数组Temp[n]和计数数组count[10],count数组第一次赋值记录下每个箱中各有多少元素,第二次赋值计算出包括当前箱子在内共有多少个元素,形象的说就是看看当前箱内记录排在第几个,对每个记录标上序号(分箱),然后从原数组R中取值,对应放入临时数组Temp中的相应位置(装箱)。
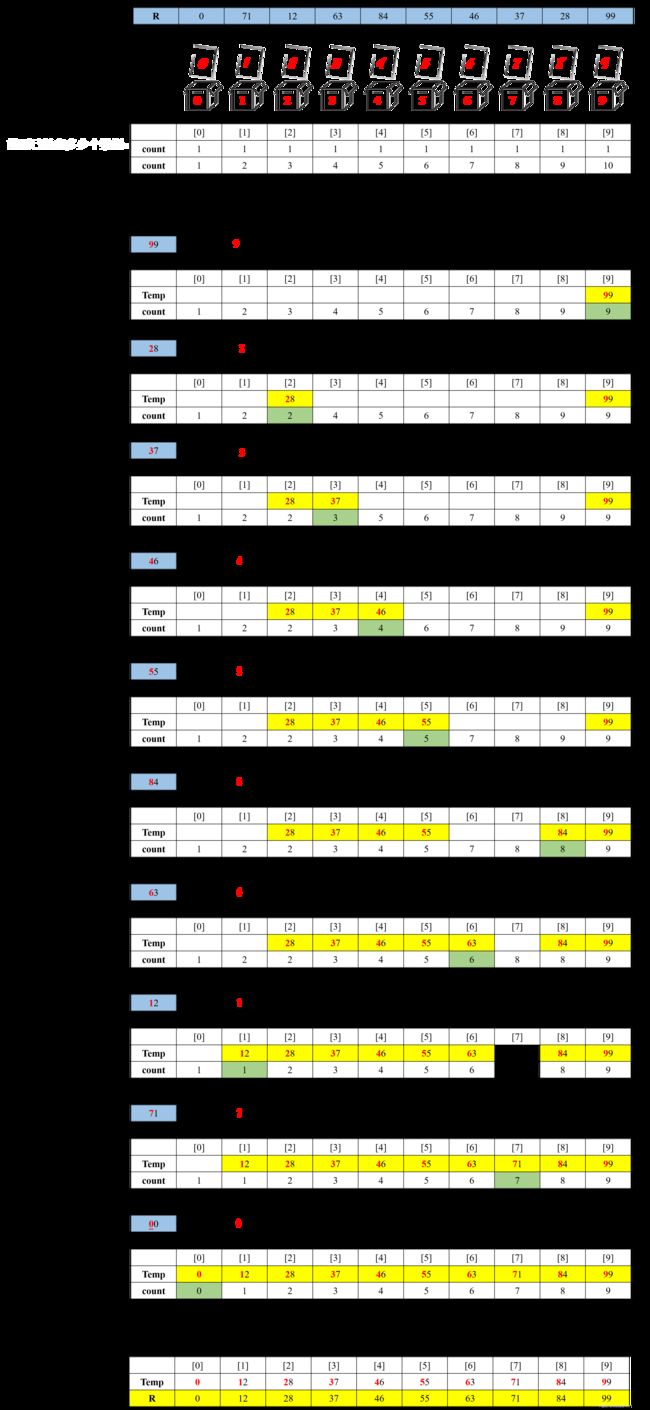
对于待排序记录 37 28 46 12 55 0 99 84 63 71 最大数99是两位数,则需进行个位、十位两趟排序。
整个过程下来可以看出,排序时没有关键字之间的比较过程,只是将关键字分配到合适的箱中,再按箱子顺序输出非空箱子里的数据。count[k]–的作用是控制一个箱子里如果有多个关键字,一个关键字输出后下一个关键字再输出时放在其前面,否则就把已经输出的覆盖掉了。
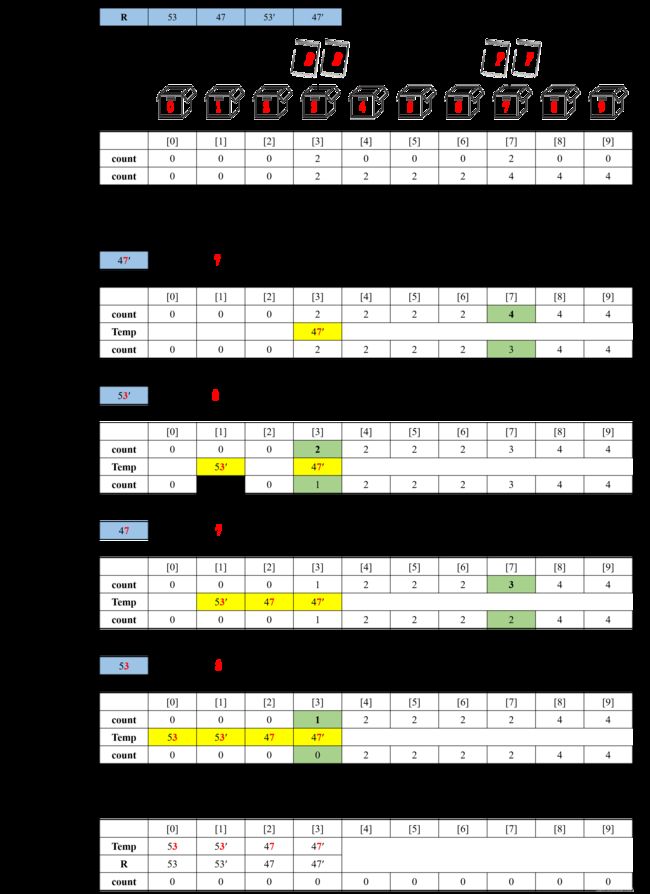
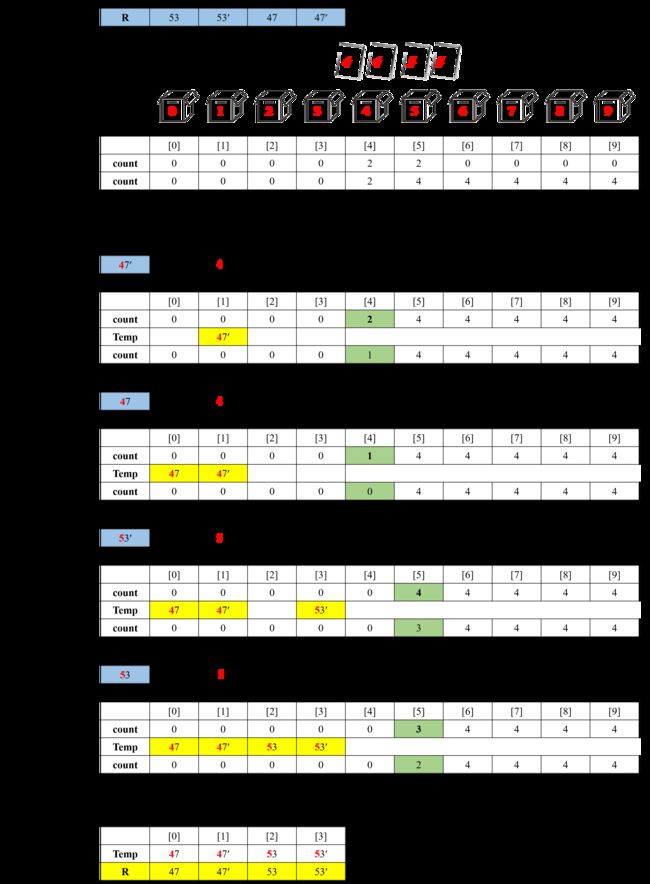
然后再举一个有些特殊性的样例 53 47 53′ 47′ 这个例子中有2组相等的关键字,可以来观察一个箱中多个关键字的操作过程和排序的稳定性。
基数排序的思路不难理解,就是按每一位数字分箱和装箱的过程,但是在程序实现中,如何分箱、如何装箱、用什么方式表示箱子都是需要思考的问题。"箱"是为了便于理解而抽象出来的,分箱的过程其实是count数组在记录每个关键字在文件中的位置,装箱的过程则是将待排序数组R中关键字取出,根据count数组的记录将关键字放入Temp数组对应位置。
参考代码(C语言)
#include分析总结
基数排序的思路来自箱排序,但对箱排序进行了一定的优化,基数排序也因此被叫做“箱子法”或“桶子法”,也有很多时候提到的箱排序其实指的就是基数排序。并且对于基数排序程序的构建方法是很多的,我使用的是数组方式作为存储结构,我参考的教材中有使用链表作为存储结构,书上把用链表作为存储结构的基数排序叫做链式基数排序。
因为基数排序使用分配的方式进行排序,所以需要依据关键字的特点进行专门的设计,比如,本例给出的基数排序只适用于自然数,对于负数、小数都不能进行排序,所以基数排序的可优化空间也很大。基数排序没有关键字之间的比较,所以省去了因比较产生的时间开销,它的时间主要消耗在修改count数组,空间开销用于建立记录数组count和临时数组Temp。
平均时间复杂度O( d ∗ ( n + k ) d*(n+k) d∗(n+k))
空间复杂度O( n + k n+k n+k)
这里n是待排序记录个数;d是分量,即排序趟数,本例都是两位数,有个位、十位2个分量,d=2;k代表基数,本例对自然数,基数取值范围0~9,所以k=10。当n较大,d较小时,即待排序记录很多,但分量较小时,基数排序十分适用。
基数排序时稳定的。原因有两方面:一方面,基数排序没有关键字之间的比较,也就没有关键字之间的交换,另一方面,前面提到了由小至大排序,从右至左扫描,由大到小排序,从左至右扫描,其实也是为了排序的稳定性考虑,若由小至大排序装箱时从左至右扫描,就会使R数组放在前面的关键字放入了Temp数组的后面位置,如样例2中第一趟排序若从左至右扫描,那第一趟的排序结果就会是 53′ 53 47′ 47 使相等关键字前后位置发生了变化,排序变得不稳定,甚至有可能导致排序出现错误。
写在最后
代码的表达形式多种多样,重点是理解排序的思想和过程,网上有许多有关排序的(个人觉得如果有一些基础的看本文上面给的图示去理解最好,更有助于建立编程的思维,视频能相对有些趣味性)
参考资料:《数据结构-用C语言描述》高等教育出版社
(只是分享个人学习时的想法和理解,如有问题还望大佬指点)