背包九讲 全部解法 详解 (01背包, 多重背包, 完全背包)
概述
给定一组物品,每种物品都有自己的重量和价值,现有一个背包,能承受的重量有限,在受限制的重量下,取若干物品,使得总价值最大。这一类问题,被称为背包问题。
01背包问题
当前有 N 件物品和一个容积为 V 的背包。已知第 i 件物品的体积是 c_i ,价值是 w_i 。 由于每种物品有且仅有一件,因此只能选择放或不放,我们称之为 01 背包问题。
现在你需要选出若干件物品,在它们的重量之和不超过 V 的条件下,使得价值总和尽可能大。
1. 定义状态dp[i][j]: 前 i个物品, 重量不超过 j的情况下所获得的最大价值
2. 写出状态转移方程: 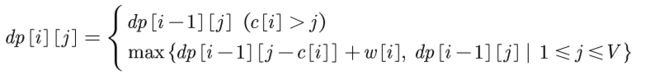
3. coding!
memset(dp, 0, sizeof(dp)); //初始化
for(int i = 1; i <= N; i++)
for(int j = 0; j <= V; j++){ //一定要从0开始, 确定边界
if(j >= c[i])
dp[i][j] = max(dp[i - 1][j - c[i]] + w[i], dp[i - 1][j]);
else
dp[i][j] = dp[i - 1][j];
}
时间复杂度: O(NV)
01背包问题的优化
时间复杂度上很难再优化了, 但空间复杂度中却存在着大量的重复计算.
仔细观察上述状态转移方程, 对于dp[i][j], 只需要dp[i-1]这一层就可以了, 而且由于是[j-c[i]], 可知我们不断需要使用左边的某一个dp, 从这个特性入手, 使用一维数组dp[j]来表示当前重量不超过 j时的最大价值
可得状态转移方程![]()
代码同时也简化了很多
for (int i = 1; i <= n; ++i)
for (int j = v; j >= c[i]; --j)
dp[j] = max(dp[j - c[i]] + w[i], dp[j]);
多重背包问题
有 N 种物品,第 i 种物品的体积是 c[i],价值是 w[i],每种物品的数量都是有限的,为 n[i]。 现有容量为 V 的背包,请你放入若干物品,在总体积不超过 V 的条件下,使总价值尽可能大。
转换01背包:
![]()
把n[i]个物品依次拆分, 转换为01背包问题求解, 时间复杂度为O(V ∑n)
转移方程如下
代码如下:
for (int i = 1; i <= N; i++)
for (int j = 0; j <= V; j++)
for (int k = 0; k <= n[i]; k++)
if (j >= c[i] * k)
dp[i][j] = max(dp[i - 1][j - c[i] * k] + w[i] * k, dp[i][j]);
//因为k不确定, 所以要和自己取, dp[i-1][j]也包含在k=0时省略的else中了
空间优化版本
for (int i = 1; i <= N; i++)
for (int j = V; j >= 0; j--)
for (int k = 0; k <= n[i]; k++)
if (j >= c[i] * k)
dp[j] = max(dp[j - c[i] * k] + w[i] * k, dp[j]);
二进制优化版本:
使用1, 2, 4 ,8, 16可以组成1-63中的任意整数, 利用这个特性, 假设第 i 个物品有 n[i] 件,我们把它分成若干组, 每一组数分别为1, 2, 4, 8…2^(k-1), n[i]-2^k+1(可能剩下的, 2^k-1为等比数列前k-1项和), 其中k便是满足n[i]-2^k +1 > 0的最大整数
可以证明, 通过若干组的组合, 一定可以组成1到n的任意个数, 从而替换了0到n[i]的枚举
复杂度降至 O(V∑logn)
//找到最大的k
int ncnt = 1;
for(int i = 1; i <= N; ++i){
int k;
for(k = 1; n[i]-(1<<k)+1 > 0; ++k){
nc[ncnt] = (1<<(k-1))*c[i];
nw[ncnt] = (1<<(k-1))*w[i];
++ncnt;
}
//查看是否还有剩余的
--k;
nc[ncnt] = (n[i]-(1<<k)+1)*c[i];
nw[ncnt] = (n[i]-(1<<k)+1)*w[i];
++ncnt;
}
//01背包
for(int i = 1; i <= ncnt; ++i){
for(int j = V; j >= nc[i]; --j){
dp[j] = max(dp[j], dp[j-nc[i]]+nw[i]);
}
}
完全背包问题
当前有 N 种物品,第 i 种物品的体积是 c[i] ,价值是 w[i] 。 每种物品的数量都是无限的,可以任意选择若干件。 现有容量为 V 的背包,请你放入若干物品,使总体积不超过 V,并且总价值尽可能大。 这就是完全背包问题,和 01 背包的区别就是物品无限多个。
转为01背包求解:
for (int i = 1; i <= N; i++)
for (int j = 0; j <= V; j++)
for (int k = 0; k * c[i] <= j; k++)
dp[i][j] = max(dp[i - 1][j - c[i] * k] + w[i] * k, dp[i][j]);
时间优化算法:
其实我们考虑一下, 由于每个物品的数量是无限的, 我们其实不用再担心dp[i][j-c[i]]被更新掉的问题, 因为即时被更新掉了, 我们也可以在下一轮再放上对应的数量

同01背包的区别仅在于dp[i][j-c[i] ]和dp[i-1][j-c[i]] (01背包), 时间复杂度O(NV)
for (int i = 1; i <= n; i++)
for (int j = 0; j <= v; j++) {
if (j >= c[i])
dp[i][j] = max(dp[i][j - c[i]] + w[i], dp[i - 1][j]);
else
dp[i][j] = dp[i - 1][j];
}
空间优化:
for (int i = 1; i <= n; i++)
for (int j = c[i]; j <= v; j++){
dp[j] = max(dp[j], dp[j-c[i]]+w[i]);
可见优化至最后, 与01背包仅仅在顺序上存在了差别
小计
背包问题的有趣的细节:
优化为一维后, 如果初始化dp[1 - n]全部为0, 最终的dp[i]意为总重量不超过m的最大价值; 而如果仅仅只把dp[0]初始化为0, 其余为 -INF, 则dp[i]意为总重量恰好为i时的最大价值