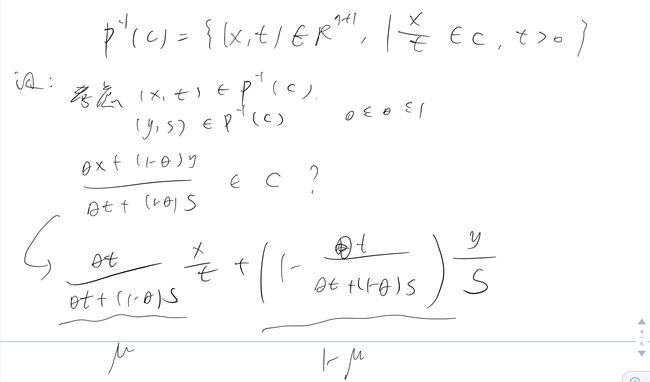交集
- 若\(S_1, S_2\)为凸,则\(S_1 \cap S_2\)也为凸。
- 进一步拓展,若\(S_a\)为凸,\(\forall a \in A\),则\(\cap_{a \in A}S_a\)为凸。
仿射函数
\(f:R^n \rightarrow R\)是仿射函数的当\(f(x)=Ax+b, A \in R^{m \times n}, b \in R^m\)。
若一个集合是凸集,经过仿射作用后还是凸集。
仿射函数的逆
- 一个凸集经过仿射函数的逆作用后还是保持凸性。
缩放和移位能保持凸性
如果\(S\)是凸集,则\(\forall a\),下面的集合也是凸集:
- \(a S = \{ax| x= \in S\}\)
- \(S + a = \{x+a|x \in S\}\)
两个集合的和是凸的
- 若\(S_1,S_2\)是凸集,则\(S_1+S_2=\{x+y|x\in S_1, y \in S_2\}\)也是凸的。
- 若\(S_1,S_2\)是凸集,则\(S_1 \times S_2=\{(x,y)|x\in S_1, y \in S_2\}\)也是凸的。
线性矩阵不等式LMI的解集是凸集
什么是线性矩阵不等式呢?
\[A(x)=x_1 A_1 + ... + x_n A_n \preccurlyeq B, \ \ \ \ \ \ B,A_i,x_i \in S^n\]
上述\(A(x)\)就是线性矩阵。
结论:\(\{x|A(x) \preccurlyeq B\}\)是凸集。
证明:
定义仿射变换:\(f(x) \triangleq B - A(x)\)。这个函数的右边中一个点由\(n\)个矩阵组成,而右边的一个点由一个矩阵组成。
因为\(S_+^n\)为凸,所以\(f^{-1}(S_+^n)\)也是凸集(因为仿射变换的逆不改变凸性)。即:
\[f^{-1}(S_+^n)=\{x| B - A(x) \succcurlyeq 0\}\]
故\(\{x|A(x) \preccurlyeq B\}\)是凸集。证毕。
椭球是球的仿射变换
其实这个很容易理解。仿射变换就是拉伸和移位。把一个球拍扁了就变成椭球了。
其椭球的定义:
\[\epsilon =\{x| (x-x_c)P^{-1}(x-x_c) \leq 1\}\]
其中\(P \in S_{++}^n\)。
下面证明如何用一个单位球变形到椭球:
单位球可以写成:\(\{u|||u||_2 \leq 1\}\)
定义仿射变换:\(f(u)=P^{\frac{1}{2}}u + x_c\),则:
\[ \begin{aligned} & \{f(u) | ||u||_2 \leq 1\} \\ =& \{P^{\frac{1}{2}}u + x_c | ||u||_2 \leq 1\}, x \triangleq P^{\frac{1}{2}} u + x_c \\ =& \{x | ||P^{\frac{1}{2}}(x-x_c)||_2 \leq 1\} \\ =& \{x | (x-x_c)^TP^{-1}(x-x_c) \leq 1\} \end{aligned} \]
透视函数
定义透视函数:
\[ \begin{aligned} & P: R^{n+1} \rightarrow R^n , dom P = R^n \times R_{++} \\ & P(z, t) = \frac{z}{t}, z \in R^n, t \in R_{++} \end{aligned} \]
- 凸集经过透视函数还是凸集。
- 任意凸集的反透视映射任是凸集。
线性分数函数
仿射映射\(g: R^n \rightarrow R^{m+1}\)
\[g(x)=\begin{bmatrix} A \\ C^T \end{bmatrix}x + \begin{bmatrix} b \\ d \end{bmatrix}\]
其中\(A \in R^{m \times n }, b \in R^m, C\in R^n, d \in R\)。透视映射:\(P: R^{m+1} \rightarrow R^m\)
根据仿射映射和透视映射,我们可以定义线性分数映射:\(f: R^n \rightarrow R^m \triangleq p \circ g\)
\[f(x)=\frac{Ax + b}{C^Tx + d}, dom f=\{x|C^Tx+d >0\}\]
- 凸集经过线性分数函数后还是凸集。