LeetCode 214. Shortest Palindrome（最短回文）

原题网址：https://leetcode.com/problems/shortest-palindrome/

Given a string S, you are allowed to convert it to a palindrome by adding characters in front of it. Find and return the shortest palindrome you can find by performing this transformation.

For example:

Given "aacecaaa", return "aaacecaaa".

Given "abcd", return "dcbabcd".

方法一：应用Manacher方法求出最长回文前缀。

public class Solution {
    public String shortestPalindrome(String s) {
        if (s == null) return null;
        if (s.length() == 0) return "";
        char[] sa = s.toCharArray();
        char[] ma = new char[sa.length*2+1];
        ma[0] = '#';
        for(int i=0, j=1; i=0; r++) {
                if (ma[i-r] != ma[i+r]) break;
                radius[i] = r;
                if (i-r==0) patch = sa.length - i;
            }
            if (rightmost < i+radius[i]) {
                rightmost = i + radius[i];
                center = i;
            }
        }
        char[] palindrome = new char[sa.length + patch];
        for(int j=0, k=sa.length-1; j

另一种实现：

public class Solution {
    public String shortestPalindrome(String s) {
        char[] sa = s.toCharArray();
        char[] ma = new char[sa.length * 2 + 1];
        Arrays.fill(ma, '#');
        for(int i = 0, j = 1; i < sa.length; i++, j += 2) {
            ma[j] = sa[i];
        }
        int[] radius = new int[ma.length];
        int center = 0;
        int rightmost = 0;
        int min = sa.length;
        for(int i = 1; i < ma.length - 1; i++) {
            int j = 0;
            if (i < rightmost) {
                j = Math.min(rightmost - i, radius[center * 2 - i]);
                radius[i] = j;
            }
            j++;
            for(; i - j >= 0 && i + j < ma.length && ma[i - j] == ma[i + j]; j++) {
                radius[i] = j;
                if (rightmost < i + j) {
                    rightmost = i + j;
                    center = i;
                }
                if (i - j == 0) min = Math.min(min, sa.length - j);
            }
        }
        StringBuilder sb = new StringBuilder(s.substring(sa.length - min));
        sb.reverse();
        sb.append(s);
        return sb.toString();
        
    }
}

其中，j = Math.min(rightmost - i, radius[center * 2 - i]);

这个地方要特别注意，容易遗忘写成 j = radius[center * 2 - i];

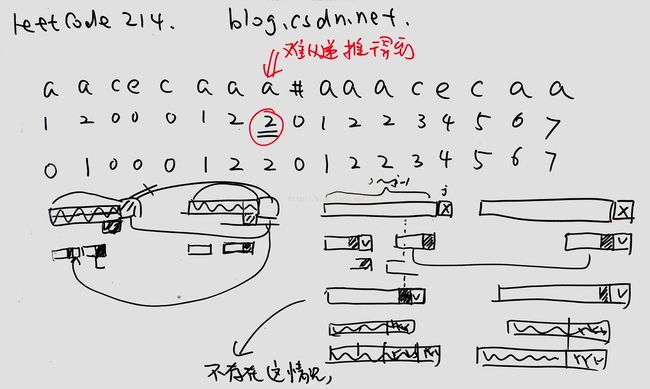
方法二：应用KMP算法找出最长回文前缀。

源代码：

public class Solution {
    public String shortestPalindrome(String s) {
        char[] ma = new StringBuilder(s).append("#").append(new StringBuilder(s).reverse().toString()).toString().toCharArray();
        int[] next = new int[ma.length];
        for(int i=1; i0 && ma[j]!=ma[i]) j=next[j-1];
            next[i] = j + (ma[j]==ma[i]? 1 : 0);
        }
        return new StringBuilder(s.substring(next[ma.length-1])).reverse().toString()+s;
    }
}

另一种实现：

public class Solution {
    public String shortestPalindrome(String s) {
        if (s.length() == 0) return s;
        StringBuilder sb = new StringBuilder(s);
        sb.reverse();
        sb.insert(0, "#");
        sb.insert(0, s);
        char[] pa = sb.toString().toCharArray();
        int[] lens = new int[pa.length];
        for(int i = 1; i < lens.length; i++) {
            int j = lens[i - 1];
            while (j > 0 && pa[j] != pa[i]) j = lens[j - 1];
            lens[i] = j + (pa[j] == pa[i] ? 1 : 0);
        }
        StringBuilder pb = new StringBuilder();
        pb.append(s.substring(lens[lens.length - 1]));
        pb.reverse();
        pb.append(s);
        return pb.toString();
    }
}

需要注意的是，这里的lens并不是单纯的最长公共前缀后缀，因为lens[0]等于0，所以只能说是KMP算法的一个变种。

如果lens定义为最长公共前缀后缀，则无法通过j = lens[j - 1]进行递推。

因此严格来定义，lens[i]是表示从0～i的字符串中，长度小于i+1的最长公共前缀后缀的长度，即不包含公共前后缀为0～i整个字符串的情况。

那么对于全不相同的字符，例如aaaa，lens[3] = 3岂不是有问题了吗？

诀窍在于我们在中间插入了“#”符号，使得这种全部相同字符的情况是不会出现的。

参考： http://blog.csdn.net/v_july_v/article/details/7041827/

此外还有很多其他关于KMP方法的讨论，请自行搜索。