《机器学习实战》学习笔记（七）之预测数值类型数据：回归

转载请注明作者和出处：http://blog.csdn.net/john_bh/
运行平台： Windows
Python版本： Python3.6
IDE： Sublime text3

一、降维技术

1.1 什么是降维

降维就是通过某种数学变换讲原始数据高维属性空间转变为一个低维“子空间”，亦称“维数约简”。
在这个子空间中样本密度大大提高，距离计算也变得更为容易。
为什么要降维呢？
因为在很多时候，人们观测或收集的数据样本虽然是高维的，但是与学习任务密切相关的也许仅是某个低维分布。
使用降维技术的好处：

• 使得数据集更易使用
• 降低很多算法的计算开销
• 去除噪声
• 使得结果易懂

1.2 降维的方法：

第一种降维的方法是主成分分析（Principal Component Analysis，PCA）。
在PCA中，数据从原来的坐标转换为新的坐标，新的坐标系的选择是有数据本身决定的。第一个新坐标轴选择的是原来数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复，重复次数为原始数据中特征的数目。

另外一种降维方法是因子分析（Factor Analysis）。
在因子分析中，我们假设在观察数据的而生成中有一些观察不到的隐变量（latent variable）。假设观察数据是这些隐变量和某些噪声的线性组合，那么隐变量的数据可能比观察数据的数目少。也就是说通过找到隐变量就可以实现数据的降维。

还有一种降维技术就是独立成分分析（Independent Component Analysis，ICA）。ICA假设数据是从N个数据源生成的，这一点和因子分析有点类似。假设数据为多个数据源的混合观察结果，这些数据源之间在统计上是相互独立的，而在PCA中只假设数据是不相关的。同因子分析一样，如果数据源的数目少于观察数据的数目，则可以实现降维的过程。

二、PCA

在介绍PAC之前，考虑一个问题：对于正交属性空间中的样本点，如何用一个超平面或者直线对所有的样本进行恰当的表达？
若存在这样的一个平面，则样本点在这个平面上是尽可能分开的。

假定数据样本进行了中心化，即 ∑ixi=0 ，再假定投影变化后得到的新坐标系为 w1,w2,...,wd ，其中 wi 是标准正交基向量， ||wi||=1,wTiwj=0(i≠j) .
我们知道样本点 xi 在新空间中超平面上的投影是 WTxi ,若使得所有样本点的投影尽可能分开，则应该使投影后样本点的方差最大化。
投影后的样本点的方差是 ∑iWTxixTiW ，则优化目标可以写为：

W=maxtr(∑iWTxixTiW)，其中WTW=I

使用拉格朗日乘子法可得：

XXTwi=λiwi

于是只需要对协方差矩阵 XXT 进行特征值分解，将求得的特征值排序： λ1≥λ2≥...≥λd ，再取 d‘ 几个特征值对应的特征向量构成的 W∗=(w1,w2,...,wd‘) ，这就是主成分分析的解。

PAC算法描述：
输入：样本集 D=x1,x2,....,xm ；低维空间维数 d,
过程：

1. 对所有样本进行去中心化： xi←xi−1m∑mi=1xi
2. 计算样本的协方差矩阵 XXT ；
3. 对协方差矩阵 XXT 做特征值分解；
4. 取最大的 d‘ 个特征值所对应的特征向量 w1,w2,...,wd‘

输出：投影矩阵 W∗=(w1,w2,...,wd‘)

降维后的低维空降的维数 d‘ 通常是由用户事先指定的，或者通过在 d‘ 值不同低维空中对分类器进行交叉验证来选取较好的 d‘ ，对PCA,还可以从重构的角度设置一个重构阈值，例如t=95%，然后选取使得下式成立的最小 d‘ 值：

∑d‘i=1λi∑di=1λi≥t

很显然低维空间和原始的高维空间必有不同，降维也注定将舍弃一部分信息，但是舍弃这部分信息往往是有必要的：一方面舍弃这部分信息之后能使样本的采样密度增大，这正是降维的主要动机；另一方面,当数据受到噪声影响时，最小的特征值所对应的特征向量往往与噪声有关，将他们舍弃能在一定程度上起到去噪的效果。

三、实例

3.1 在Numpy中实现PCA

将数据转化为前N个主要成分的伪代码如下：

去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值从大到小排序
保留前N个特征向量
将数据转换到上述N个特征向量构建的新空间中

新建文件pca.py文件，具体代码实现如下：

# -*- coding:utf-8 -*-

from numpy import *
import matplotlib
import matplotlib.pyplot as plt

def loadDataSet(fileName, delim):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [list(map(float,line)) for line in stringArr]
    return mat(datArr)

def pca(dataMat, topNfeat=9999999):
    meanVals=mean(dataMat,axis=0)   #求每一列的均值
    meanRemoved=dataMat-meanVals   #对所有样本进行去中心化
    covMat = cov(meanRemoved, rowvar=0)    #计算协方差矩阵
    eigVals, eigVects = linalg.eig(mat(covMat))    #求解特征值和特征向量
    eigValInd = argsort(eigVals)  # 对特征值从小到大排序
    eigValInd = eigValInd[:-(topNfeat + 1):-1]
    redEigVects = eigVects[:, eigValInd]  # 保留前N个大的特征向量
    lowDDataMat = meanRemoved * redEigVects
    reconMat = (lowDDataMat * redEigVects.T) + meanVals    # 将数据转换到新空间
    return lowDDataMat, reconMat

if __name__=="__main__":
    fileName="testSet.txt"
    delim = '\t'
    dataMat=loadDataSet(fileName,delim)
    lowDDataMat, reconMat=pca(dataMat,1)

    fig = plt.figure()
    ax = fig.add_subplot(111)
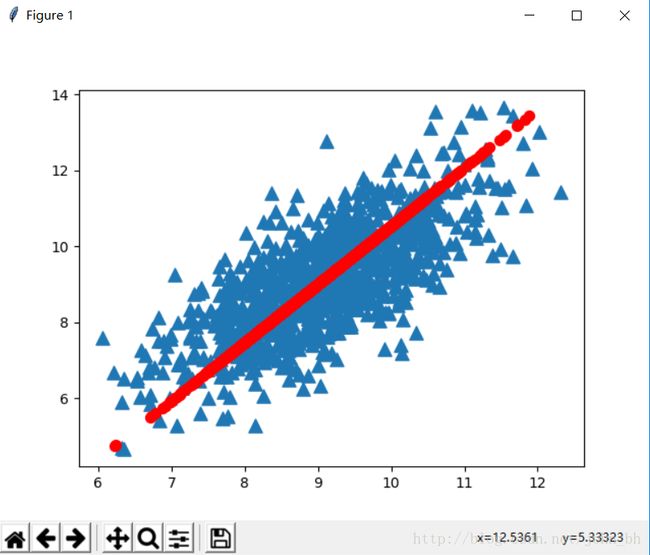
    ax.scatter(array(dataMat[:, 0]), array(dataMat[:, 1].tolist()), marker='^', s=90)
    ax.scatter(array(reconMat[:, 0]), array(reconMat[:, 1].tolist()), marker='o', s=50, c='red')
    plt.show()

程序运行结果如下如所示：

3.2 利用PCA对半导体制造数据降维

数据集中包含590个特征，而且数据中还有很多缺失值，这些缺失值以NaN标识，这里我们用平均值来代替NaN，而平均值是由那些非NaN得到的。具体代码实现如下：

def replaceNanWithMean():
    datMat = loadDataSet('secom.data', ' ')
    numFeat = shape(datMat)[1]
    for i in range(numFeat):
        meanVal = mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i]) #计算所有非NaN的均值
        datMat[nonzero(isnan(datMat[:,i].A))[0],i] = meanVal  #将所有NaN置为平均值
    return datMat
if __name__=="__main__":    
    dataMat=replaceNanWithMean()
    meanVals = mean(dataMat, axis=0)
    meanRemoved = dataMat - meanVals  # 去除均值
    covMat = cov(meanRemoved, rowvar=0)    #计算协方差矩阵
    eigVals, eigVects = linalg.eig(mat(covMat))    #计算特征值和特征向量
    eigValInd = argsort(eigVals)  # 对特征值从小到大排序
    eigValInd = eigValInd[::-1]  # 反转
    sortedEigVals = eigVals[eigValInd]
    total = sum(sortedEigVals)
    varPercentage = sortedEigVals / total * 100

    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(range(1, 21), varPercentage[:20], marker='^')
    plt.xlabel(U'主成分数目',fontproperties='SimHei')
    plt.ylabel(U'方差的百分比',fontproperties='SimHei')
    plt.show()

我们这里计算了一下前20个主成分总方差百分比，比把它显示出来了，运行结果如下如所示：

从图中可以看出，大部分的方差都包含在前面几个主成分中，舍弃后面的主成分并不会损失太多信息，如果保留了前6个主成分，则数据集可以从590个特征约简到6个特征，大概实现了100：1的压缩。另外由于舍弃了噪声主成分，将后面的主成分去除噪声使得数据更加干净。

四、总结

降维技术使得数据变得更易使用，并且他们往往能够取出数据中的噪声，使得其他机器学习任务更加精确。降维往往只做数据预处理步骤，在数据应用到其他算法之前清洗数据。

PCA可以从数据中识别主要特征，它是通过沿着数据最大方差方向旋转坐标轴来实现的。选择方差最大的方向作为第一条坐标轴，后续坐标轴则与前面的坐标轴正交，而协方差矩阵上的特征值分析可以用一系列的正交坐标轴来获取。

优点：降低数据的复杂性，识别最重要的多个特征
缺点：不一定需要，且可能损失有用信息
适用数据类型：数值型数据