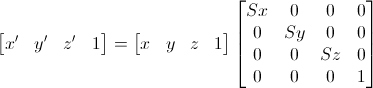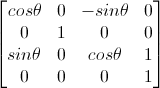坐标变换 及矩阵变换
为了对一个点进行变换(平移、伸缩、旋转等),可以用一个4 × 4 的的变换矩阵来表示,如最常见的是使用一个模型视图变换矩阵,来变换点、线、多边形以及其它几何体,也可以变换多边形表面的切向量。变换思路如下:设置一个4 × 4 的矩阵中元素的值,使其表示某一具体的变换。然后将某一点的坐标或者某一向量的分量放入一个1 × 4 的行向量 v 中。乘积 vX 就生成了经过变换的向量 v˜ ,例如,如果 X 表示沿着 x 轴平移10个单位, v=[2,6,−3,1] ,则乘积 vX=v˜=[12,6,−3,1] 。
前面提到了将某一点的坐标或者某一分量的各分量放入一个1 × 4的行向量 v 中。但是在几何学中,表示3D空间中的某点信息是使用3个分量(XYZ)来表示的!为了使向量-矩阵相乘有意义,我们必须将3D的点或向量拓展为4D行向量。
如何使用第四个分量?这个分量我们用w表示,其中w叫做齐次坐标。取值为0或者1。当W分量为1时,是为了保证点的平移变换能正确进行。而对于向量,没有必要进行平移变换,而将W分量设为0是为了防止对向量实施平移变换。
PS:
拓展后的4D向量被称为齐次向量,因此齐次向量即可以表示点,也可以表示向量,所以注意本文提到的名词“向量时,注意区分我指的是点还是向量,一般来说,下文提到的”向量“时,基本上指代的是点。
有时,我们所定义的矩阵改变了一个向量的分量w的值(即 w≠0 且 w≠1 )如下所示:
P=[p1,p2,p3,1]⎡⎣⎢⎢1000010000100010⎤⎦⎥⎥=[p1,p2,p3,p3]=P′ 对于 p3≠0 和 p3≠1 的情况
可见, w=p3 。当 w≠0 且 w≠1 时,就称该变量处于齐次空间中,以区别3D空间。将齐次空间的向量映射回3D空间的方法是:用w分量去除该齐次向量的每一个分量。例如将齐次空间的向量 (x,y,z,w) 映射回3D向量x的方法如下:
在进行3D编程是,如果涉及到透视投影,则经常需要将向量由齐次空间映射到3D空间。该操作发生在顶点变换步骤的透视除法环节。在OpenGL中,一个典型的顶点变换步骤如下:
可见,对顶点的变换都是通过矩阵来完成的,下面讨论模型视图矩阵的具体形式。
平移矩阵
要想将向量(x,y,z,1)沿着 x 轴平移 px 个单位,沿着 y 轴平移 py 个单位,沿着 z 平移 pz 个单位,只需要将该向量与如下矩阵相乘:
该平移矩阵的逆矩阵可以简单地对平移向量p取负得到。
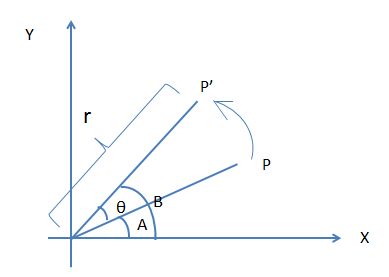
旋转矩阵
我们可以用如下3个矩阵将一个向量分别绕着x,y,z轴旋转 θ 弧度。当沿着旋转轴指向原点的方向观察时,角度是按顺时针方向度量的。
旋转矩阵R的逆矩阵与其转置相等,即 RT=R−1 。俱备这样特点的矩阵称为正交矩阵。
比例变换矩阵
如果想让一个向量沿着x、y、z轴分别放大 qx 、 qy 、 qz 倍,可令该向量与如下矩阵相乘:
如果将比例矩阵的各个缩放因子取倒数,就得到该矩阵的逆矩阵。
几何变换的组合
经常需要对向量实施一系列的变换。例如我们可能先对向量进行缩放,然后在进行旋转,最后平移到所期望的位置。
这个过程的每一步都是通过让向量乘以一个矩阵来实现,矩阵的一个最关键的优点是,可以借助矩阵乘法将几种变换组合到一个变换矩阵。
例如,当我们先对向量p实施比例变换,乘以比例变换矩阵S;在对变换后的向量实施旋转变换,乘以旋转变换矩阵R:最后对变量实施平移变换,乘以平移变换矩阵T,最后得到向量 p′′′ :
我们可以向全部的变换组合为一种变换,然后应用该变换,得到向量 p˜ :
则可以验证: p′′′=p˜
法线的变换矩阵
在着色器中执行光照计算时,不仅需要我们指定顶点坐标,还需要我们去指定法线向量。对于顶点坐标,在着色器中对其施加模型视图变换和投影变换即可得到变换后的顶点坐标,但是对于法向量的变换矩阵却与顶点的变换矩阵不一样!
这是因为法线向量会随着我们的平移和旋转发生变化。比如说,如果我们忽略旋转并且假设做了一个(0,0,-5)的平移,那么法线向量(0,0,1)就会变成(0,0,-4),这不仅长度不对而且根本就指向了错误的方向!这里也许我们可以将法线向量的w分量设为0,这样就可以忽略掉那些移位变换。但是不幸的是,当模型视图矩阵包含不同的空间变换时,尤其是缩放和扭曲时,它将不再有用。比如说,如果模型视图矩阵将我们要绘制的物体放到两倍大小,那法线向量也会被拉伸,即使我们将w分量设为0。这会导致严重的光照错误。
在OpenGL中计算法线向量的变换矩阵的方法是:先求出模型视图矩阵的逆矩阵,然后再对求出的逆矩阵转置。这样就可以得到正确的变换矩阵。这样可以去掉矩阵中非正交的因素。
证明方法如下:
假设世界坐标系(未变换前)中的某条切线向量是T,法线向量是N。那么由他们是垂直的可得到: TT⋅N=0
假设他们变换到视图坐标系中后分别是 T′ 和 N′ 。那么他们应该仍然是相互垂直的: T′T⋅N′=0
假设切线向量和法线的变换矩阵为M、G。则有: (M⋅T)T⋅(G⋅N)=0
进一步推出: TT⋅MT⋅G⋅N=0
由于 TT⋅N=0 ,因此我们猜想 MT⋅G=0 .因此:
即:应用于法线向量的变换矩阵是顶点变换矩阵的逆转置矩阵。
注意,在上面求证法线的变换矩阵的时候,是讨论OpenGL中的情况,在OpenGL中,对某一顶点实施变换时,是通过一个矩阵乘以顶点实现的,即 M⋅v=v′ ,其中,M是变换矩阵,v和 v′ 分别是变换前后的顶点。所以对于上面的证明过程有 M⋅T=T′ 而不是 T⋅M=T′ .
由于刚才提到的原因,所以在使用OpenGL编程时,我们用代码制定了一系列变换,但是最后指定的变换会最先应用到顶点上。
考虑下面的代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glMultMatrixf(N);
glMultMatrixf(M);
glMultMatrixf(L);
glBegin(GL_POINTS);
glVertex3f(v);
glEnd();
|
经过变换之后的顶点是 N⋅M⋅L⋅v ,也就是说,v首先与L相乘, L⋅v 的结果再与M相乘, M⋅L⋅v 再与N相乘,顶点v的变换是按照相反的顺序发生。
**********************************
参考:
《DirectX 9.0 3D游戏开发编程基础》
《OpenGL编程指南 第七版》
OpenGL法线变换详解
3D变换中法向量变换矩阵的推导
几何变换详解[转]
2012-10-23 10:59:44| 分类: 图形学|举报|字号 订阅