GloVe模型

1、词向量学习算法有两个主要的模型族：

• 基于全局矩阵分解的方法，如LSA：
  优点：能够有效的利用全局的统计信息；
  缺点：在单词类比任务中（如国王VS王后类比于男人VS女人）中表现相对较差；
• 基于局部上下文窗口的方法，如word2vec：
  优点：在单词类比任务中表现较好；
  缺点：因为word2vec在独立的局部上下文窗口上训练，因此难以利用单词的全局统计信息；

GloVe结合了LSA算法和word2vec算法的优点，即考虑了全局统计信息又利用了局部上下文。

2、GloVe模型原理

用$P(w_j|w_i)$表示数据集中以$w_i$为中心词生成背景词$w_j$的条件概率，并记作$P_{ij}$，作为源于某大型语料库的真实例子，下表中列举了两组分别以“ice”（冰）和“steam”（蒸汽）作为中心词的条件概率以及它们之间的比值。

$w_k$	$p_1=P(w_k\mid "ice")$	$p_2=P(w_k\mid "steam")$	$p_1/p_2$
“solid”(固体)	0.00019	0.000022	8.9
“gas” (气体)	0.000066	0.00078	0.085
“water”(水)	0.003	0.0022	1.36
“fashion”(时尚)	0.000017	0.000018	0.96

我们可以观察到以下现象：

• 对于与“ice”相关而与“steam”不相关的词$w_k$，比如$w_k$=“solid”（固体），我们期望条件概率比值较大，如上表中的值8.9；
• 对于与“ice”不相关而与“steam”相关的词$w_k$，比如$w_k$=“gas”（气体），我们期望条件概率比值较小，如上表中的值0.085；
• 对于与“ice”和“steam”都相关的词$w_k$，如$w_k$=“water”（水），我们期望条件概率比值接近1，如上表中的值1.36；
• 对于与“ice”和“steam”都不相关的词$w_k$，比如$w_k$=“fashion”（时尚），我们期望条件概率比值接近1，如上表中的值0.96；

由此可见，条件概率比值能比较直观地表达词与词之间的关系，我们可以构建一个词向量函数使他能够有效拟合条件概率比值。我们知道，任意一个这样的比值需要3个词$w_i$、$w_j$和$w_k$。以$w_i$和$w_j$为中心词的条件概率比值为$p_{i,k}/p_{j,k}$。我们可以找到一个向量函数，它使用词向量来拟合这个条件概率比值：

$$F\left({\mathbf{w}}_i,{\mathbf{w}}_j,{\mathbf{w}}_k\right)\approx \mathrm{Rati}{o}_{i,j}^k=\frac{P_{i,k}}{P_{j,k}}$$

这里函数f可能的设计并不唯一，我们只需要考虑一种较为合理的可能性。注意到条件概率比值是一个标量，同时f函数是用于评估中心词$w_i$和$w_j$的差异，因此我们可以将f函数限制为一个向量内积的标量函数：

$$F\left({\mathbf{w}}_i-{\mathbf{w}}_j,{\mathbf{w}}_k\right)=F\left({\left({\mathbf{w}}_i-{\mathbf{w}}_j\right)}^T{\mathbf{w}}_k\right)=F\left({\mathbf{w}}_i^T{\mathbf{w}}_k-{\mathbf{w}}_j^T{\mathbf{w}}_k\right)=\frac{P_{i,k}}{P_{j,k}}$$

上式左边为差的形式，右边为商的形式，因此联想到指数函数exp(.)。即F(.)函数的形式为：

$$exp({\mathbf{w}}_i^T{\mathbf{w}}_k-{\mathbf{w}}_j^T{\mathbf{w}}_k)=\frac{P_{ik}}{P_{jk}}$$

上式可以转化为：

$${\mathbf{w}}_i^T{\mathbf{w}}_k-{\mathbf{w}}_j^T{\mathbf{w}}_k=\log P_{i,k}-\log P_{j,k}$$

要使上式成立，只需要令${\mathbf{w}}_i^T{\mathbf{w}}_k=\log P_{i,k}$，${\mathbf{w}}_j^T{\mathbf{w}}_k=\log P_{j,k}$即可。

向量的内积具有对称性，即${\mathbf{w}}_i^T{\mathbf{w}}_k={\mathbf{w}}_k^T{\mathbf{w}}_i$，考虑到$P_{i,k}=\frac{x_{i,k}}{x_i}$，而$\log \frac{X_{i,k}}{X_i}\ne \log \frac{X_{k,i}}{X_k}$，即$\log P_{i,k}\ne \log P_{k,i}$，为了解决这个问题，在公式$\log \frac{X_{i,k}}{X_i}\ne \log \frac{X_{k,i}}{X_k}$左右两边分别减去$log{X}_k$和$log{X}_i$，这样就可以得到左右相等的公式：

$$\log \frac{X_{i,k}}{X_i}-log{X}_k=\log \frac{X_{k,i}}{X_k}-log{X}_i$$

即

$$log{X}_{i,k}-log{X}_i-log{X}_k=log{X}_{k,i}-log{X}_k-log{X}_i$$

令${\mathbf{w}}_i^T{\mathbf{w}}_k=log{X}_{i,k}-log{X}_i-log{X}_k$，则可以满足以上提及的对称性。

同时，对于${\mathbf{w}}_i^T{\mathbf{w}}_k$和${\mathbf{w}}_j^T{\mathbf{w}}_k$，需要满足条件：

$${\mathbf{w}}_i^T{\mathbf{w}}_k-{\mathbf{w}}_j^T{\mathbf{w}}_k=\log P_{i,k}-\log P_{j,k}$$

分别将${\mathbf{w}}_i^T{\mathbf{w}}_k=log{X}_{i,k}-log{X}_i-log{X}_k$和${\mathbf{w}}_j^T{\mathbf{w}}_k=log{X}_{j,k}-log{X}_j-log{X}_k$代入上述公式左端即可推导出右边的结果。

我们令$b_i=log{X}_i$，令$b_k=log{X}_k$，则可以得到论文中的公式，即：

$$\log X_{i,k}={\mathbf{w}}_i^T{\mathbf{w}}_k+b_i+{\tilde{b}}_k$$

但是上面的公式仅仅是理想状态，实际上只能要求左右两边尽可能相等，于是设计代价函数为：

$$J=\sum _{i,k}{\left({\mathbf{w}}_i^T{\mathbf{w}}_k+b_i+{\tilde{b}}_k-\log X_{i,k}\right)}^2$$

公式中的$\mathbf{w},b,\tilde{b}$均为模型参数，需要通过训练得到。

根据经验，如果两个词共现的次数越多，则这两个词在代价函数中的影响就越大，因此可以设计一个权重函数$f(\cdot )$来对代价函数中的每一项进行加权，权重为共现次数的函数：

$$J=\sum _{i,k}f\left(X_{i,k}\right){\left({\mathbf{w}}_i^T{\mathbf{w}}_k+b_i+{\tilde{b}}_k-\log X_{i,k}\right)}^2$$

公式中的权重函数应该符合三个条件：

1. $f(0)=0$，即如果两个词没有共现过，则权重为0，这是为了确保${\lim }_{x\to 0}f(x){\log }^{2}x$是有限值；
2. $f(\cdot )$是非递减的，即两个词共现次数越大，则权重越大；
3. $f(\cdot )$对于较大的$X_{i,k}$不能取太大的值，即有些单词共现次数非常大（如单词“的”与其它词的组合），但是他们的重要性并不是很大；

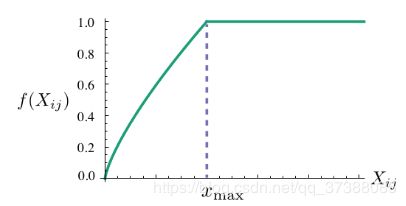
因此论文中根据以上三个条件设计了权重函数$f(\cdot )$的形式为：

$$f(x)=\{\begin{array}{ll}{\left(\frac{x}{x_{\max }}\right)}^{\alpha }& \text{ if }x<x_{\max }\\ 1,& \text{ otherwise }\end{array}$$

GloVe论文中给出函数$f(\cdot )$的参数$\alpha$和$x_{max}$的经验值为：

$$\alpha =\frac{3}{4},x_{\max }=100$$

3、GloVe模型共现矩阵生成——代码简单实现

from torch.utils import data
import os
import numpy as np
import pickle  # 用于保存数据

min_count = 50  # 用于去除低频词

# 数据集加载
data = open("./data/text8.txt").read()
data = data.split()
# 构建word2id并去除低频词
word2freq = {}  # 保存每个词的词频的字典
for word in data:
    if word2freq.get(word)!=None:
        word2freq[word] += 1
    else:
        word2freq[word] = 1
word2id = {}  # key是每个词，value是每个词对应的id
for word in word2freq:
    if word2freq[word]<min_count:  # 如果该词的词频小于min_count则抛弃
        continue
    else:
        if word2id.get(word)==None:
            word2id[word]=len(word2id)

# 构建共现矩阵
vocab_size = len(word2id)  # 统计词表的词的个数
comat = np.zeros((vocab_size,vocab_size))  # 词共现矩阵，矩阵大小为[词个数，词个数]，初始全为零
print(comat.shape)

window_size = 2  # 中心词的窗口

# 构建共现矩阵
for i in range(len(data)):
    if i%1000000==0:
        print (i,len(data))
    if word2id.get(data[i])==None:  # 如果该词不在word2id字典中，则表示是低频词，忽略
        continue
    w_index = word2id[data[i]]  # 获得该词对应的id
    for j in range(max(0,i-window_size),min(len(data),i+window_size+1)):
        if word2id.get(data[j]) == None or i==j:  # 如果是低频词或者是词自身
            continue
        u_index = word2id[data[j]]
        comat[w_index][u_index]+=1

# np.nonzero()的作用是将非零的位置找出来
# np.transpose()的作用是转换为矩阵
coocs = np.transpose(np.nonzero(comat))

# 生成训练集和Label
labels = []
for i in range(len(coocs)):
    if i%1000000==0:
        print (i,len(coocs))
    labels.append(comat[coocs[i][0]][coocs[i][1]])
labels = np.array(labels)

# 保存结果
np.save("./data/data.npy",coocs)
np.save("./data/label.npy",labels)
pickle.dump(word2id,open("./data/word2id","wb"))

4、GloVe模型简单实现

import torch
import torch.nn as nn

class glove_model(nn.Module):
    def __init__(self,vocab_size,embed_size,x_max,alpha):
        # vocab_size是词表大小
        # embed_size是词嵌入的维度
        # x_max和alpha是损失函数中f(.)的参数
        super(glove_model, self).__init__()
        self.vocab_size = vocab_size
        self.embed_size = embed_size
        self.x_max = x_max
        self.alpha = alpha
        self.w_embed = nn.Embedding(self.vocab_size,self.embed_size).type(torch.float64) # 中心词向量

        self.w_bias = nn.Embedding(self.vocab_size,1).type(torch.float64) # 中心词bias

        self.v_embed = nn.Embedding(self.vocab_size, self.embed_size).type(torch.float64) # 周围词向量

        self.v_bias = nn.Embedding(self.vocab_size, 1).type(torch.float64) # 周围词bias
    def forward(self, w_data,v_data,labels):
        w_data_embed = self.w_embed(w_data) # bs*embed_size
        w_data_bias = self.w_bias(w_data) # bs*1
        v_data_embed = self.v_embed(v_data)
        v_data_bias = self.v_bias(v_data)
        weights = torch.pow(labels/self.x_max,self.alpha) # 权重生成
        weights[weights>1]=1 
        loss = torch.mean(weights*torch.pow(torch.sum(w_data_embed*v_data_embed,1)+w_data_bias+v_data_bias-
                                 torch.log(labels),2)) # 计算loss
        return loss