算法1-啊哈算法!
1.排序
首先这里会有一个简单的排序算法。
最快最简单的排序——桶排序
问题:0-10内的数排序,假如有五个人的分数为为9,1,2,4,5
思路:
- 首先我们需要申请一个大小为 11 的数组 int a[11],编号从 a[0]~a[10]。刚开始的时候,我们将 a[0]~a[10]都初始化为 0,表示这些分数还都没有人得过。例如 a[0]等于 0 就表示目前还没有人得过 0 分,同理 a[1]等于 0 就表示目前还没有人得过 1 分…a[10]等于 0 就表示目前还没有人得过 10 分。
- 接下来就开始处理每一个人的分数,那么现在a[0]-a[10]的值为{0,1,1,0,1,1,0,0,0,1,0},表示1,2,4,5,9出现1次。
- 判断啊a[0]-a[10]根据值打印下表次数,打印结果为排序结果
代码:
#include
int main()
{
int a[11],i,j,t;
for(i=0;i<=10;i++)
a[i]=0; //初始化为0
for(i=1;i<=5;i++){
scanf("%d",&t); //把每一个数读到变量t中
a[t]++; //进行计数
}
for(i=0;i<=10;i++) //依次判断a[0]~a[10]
for(j=1;j<=a[i];j++) //出现了几次就打印几次
printf("%d ",i);
getchar();
getchar();//这里的getchar();用来暂停程序,以便查看程序输出的内容//也可以用system("pause");等来代替
return 0;
}
上面是一个简单的排序算法,i假如是0-m数的排序,需要m个桶来装数出出现的次数,假如需要排序的数个数为n个,看一下时间复杂度的问题: 初始化-m次 , 读变量-n次,打印:m+n次我们用大写字母 O 来表示时间复杂度,因此该算法的时间复杂度是 O(m+n+m+n)即 O(2*(m+n))。我们在说时间复杂度的时候可以忽略较小的常数,最终桶排序的时间复杂度为 O(m+n)。还有一点,在表示时间复杂度的时候,n 和 m通常用大写字母即 O(M+N)。
桶排序从 1956 年就开始被使用,该算法的基本思想是由E.J.Issac 和 R.C.Singleton 提出来的。之前我说过,其实这并不是真正的桶排序算法,真正的桶排序算法要比这个更加复杂。但是考虑到此处是算法讲解的第一篇,我想还是越简单易懂越好,真正的桶排序留在以后再聊吧。
冒泡排序
上面的算法只能处理简单的问题,而且比较浪费空间,而且无法进行小数排序。
冒泡排序的基本思想是:每次比较两个相邻的元素,如果它们的顺序错误就把它们交换
过来
问题:将 12 35 99 18 76 这 5 个数进行从大到小的排序。
思路:
- 首先比较第 1 位和第 2 位的大小,现在第 1 位是 12,第 2 位是 35。发现 12 比 35 要小因为我们希望越小越靠后嘛,因此需要交换这两个数的位置。交换之后这 5 个数的顺序是35 12 99 18 76。
- 按照刚才的方法,继续比较第 2 位和第 3 位的大小,第 2 位是 12,第 3 位是 99。12 比99 要小,因此需要交换这两个数的位置。交换之后这 5 个数的顺序是 35 99 12 18 76。
- 根据刚才的规则,继续比较第 3 位和第 4 位的大小,如果第 3 位比第 4 位小,则交换位置。交换之后这 5 个数的顺序是 35 99 18 12 76。
- 最后,比较第 4 位和第 5 位。4 次比较之后 5 个数的顺序是 35 99 18 76 12。
- 经过四次比较之后,12最小值已经移动到最后的位置。每次都是比较相邻的两个数,如果后面的数比前面的数大,则交换这两个数的位置。一直比较下去直到最后两个数比较完毕后,最小的数就在最后一个了。就如同是一个气泡,一步一步往后“翻滚”,直到最后一位。所以这个排序的方法有一个很好听的名字冒泡排序。
代码:
#include
int main()
{
int a[100],i,j,t,n;
scanf("%d",&n); //输入一个数n,表示接下来有n个数
for(i=1;i<=n;i++) //循环读入n个数到数组a中
scanf("%d",&a[i]);
//冒泡排序的核心部分
for(i=1;i<=n-1;i++) //n个数排序,只用进行n-1趟
{
for(j=1;j<=n-i;j++) //从第1位开始比较直到最后一个尚未归位的数,想一想为什么到n-i就可以了。
{
if(a[j] 假如我们这里需要输出分数对应的名字。
代码修改如下:
#include
struct student
{
char name[21];
char score;
};//这里创建了一个结构体用来存储姓名和分数
int main()
{
struct student a[100],t;
int i,j,n;
scanf("%d",&n); //输入一个数n
for(i=1;i<=n;i++) //循环读入n个人名和分数
scanf("%s %d",a[i].name,&a[i].score);
//按分数从高到低进行排序
for(i=1;i<=n-1;i++)
{
for(j=1;j<=n-i;j++)
{
if(a[j].score 冒泡排序的核心部分是双重嵌套循环。不难看出冒泡排序的时间复杂度是 O(N 2 )。这是
一个非常高的时间复杂度。
快速排序
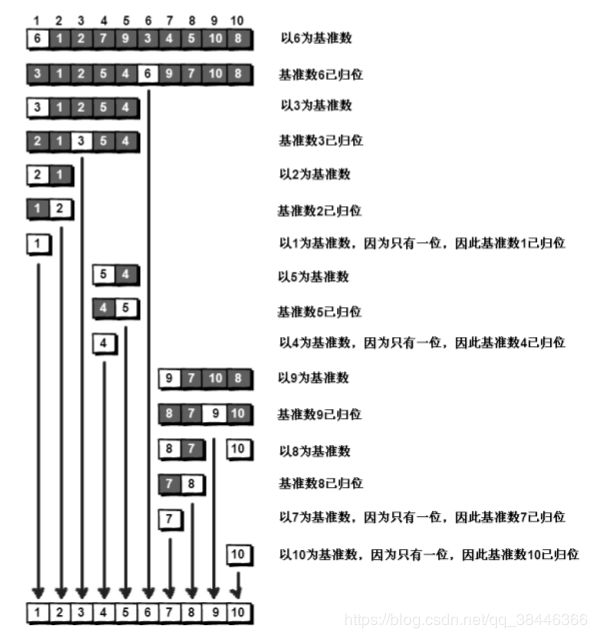
问题:对“6 1 2 7 9 3 4 5 10 8”这 10 个数进行排序。
思路:
- 首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,这就是一个用来参照的数,为了方便,就让第一个数 6 作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在 6 的右边,比基准数小的数放在 6 的左边。
- 分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于 6 的数,再从左往右找一个大于 6 的数,然后交换它们。这里可以用两个变量 i 和 j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵 i”和“哨兵 j”。刚开始的时候让哨兵 i 指向序列的最左边(即 i=1),指向数字 6。让哨兵 j 指向序列的最右边(即 j=10),指向数字 8。
- 首先哨兵 j 开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵 j 先出动,这一点非常重要(请自己想一想为什么)。哨兵 j 一步一步地向左挪动(即 j++),直到找到一个小于 6 的数停下来。接下来哨兵 i 再一步一步向右挪动(即 i++),直到找到一个大于 6的数停下来。最后哨兵 j 停在了数字 5 面前,哨兵 i 停在了数字 7 面前。
- 到此,第一次交换结束。接下来哨兵 j 继续向左挪动(再次友情提醒,每次必须是哨兵j 先出发)。他发现了 4(比基准数 6 要小,满足要求)之后停了下来。哨兵 i 也继续向右挪动,他发现了 9(比基准数 6 要大,满足要求)之后停了下来。此时再次进行交换,交换之后的序列如下。6 1 2 5 4 3 9 7 10 8。
- 第二次交换结束,“探测”继续。哨兵 j 继续向左挪动,他发现了 3(比基准数 6 要小,满足要求)之后又停了下来。哨兵 i 继续向右移动,糟啦!此时哨兵 i 和哨兵 j 相遇了,哨兵 i 和哨兵 j 都走到 3 面前。说明此时“探测”结束。我们将基准数 6 和 3 进行交换。交换之后的序列如下。3 1 2 5 4 6 9 7 10 8。
- 现在先来处理 6 左边的序列吧。左边的序列是“3 1 2 5 4”。请将这个序列以 3 为基准数进行调整,使得 3 左边的数都小于等于 3,3 右边的数都大于等于 3。
- 现在 3 已经归位。接下来需要处理 3 左边的序列“2 1”和右边的序列“5 4”。对序列“2 1”以 2 为基准数进行调整,处理完毕之后的序列为“1 2”,到此 2 已经归位。序列“1”只有一个数,也不需要进行任何处理。至此我们对序列“2 1”已全部处理完毕,得到的序列是“1 2”。序列“5 4”的处理也仿照此方法,最后得到的序列如下。1 2 3 4 5 6 9 7 10 8,对于序列“9 7 10 8”也模拟刚才的过程,直到不可拆分出新的子序列为止。最终将会得到这样的序列。1 2 3 4 5 6 7 8 9 10。
代码:
#include
int a[101],n;//定义全局变量,这两个变量需要在子函数中使用
void quicksort(int left,int right)
{
int i,j,t,temp;
if(left>right)
return;
temp=a[left]; //temp中存的就是基准数
i=left;
j=right;
while(i!=j)
{
//顺序很重要,要先从右往左找
while(a[j]>=temp && i 例子
问题:
小哼的学校要建立一个图书角,老师派小哼去找一些同学做调查,看看同学们都喜欢读哪些书。小哼让每个同学写出一个自己最想读的书的 ISBN 号(你知道吗?每本书都有唯一的 ISBN 号,不信的话你去找本书翻到背面看看)。当然有一些好书会有很多同学都喜欢,这样就会收集到很多重复的 ISBN 号。小哼需要去掉其中重复的 ISBN 号,即每个 ISBN 号只保留一个,也就说同样的书只买一本(学校真是够抠门的)。然后再把这些 ISBN 号从小到大排序,小哼将按照排序好的 ISBN 号去书店买书。请你协助小哼完成“去重”与“排序”的工作。
输入有 2 行,第 1 行为一个正整数,表示有 n 个同学参与调查(n≤100)。第 2 行有 n个用空格隔开的正整数,为每本图书的 ISBN 号(假设图书的 ISBN 号在 1~1000 之间)。
输出也是 2 行,第 1 行为一个正整数 k,表示需要买多少本书。第 2 行为 k 个用空格隔开的正整数,为从小到大已排好序的需要购买的图书的 ISBN 号。
最后,程序运行的时间限制为 1 秒。
思路:
- 解决这个问题的方法大致有两种。第一种方法:先将这 n 个图书的 ISBN 号去重,再进
行从小到大排序并输出;第二种方法:先从小到大排序,输出的时候再去重。这两种方法都
可以。 - 先来看第一种方法。通过第一节的学习我们发现,桶排序稍加改动正好可以起到去重的
效果,因此我们可以使用桶排序的方法来解决此问题。 - 第二种方法我们需要先排序再去重。排序我们可以用冒泡排序或者快速排序。
代码:
第一种:
#include
int main()
{
int a[1001],n,i,t;
for(i=1;i<=1000;i++)
a[i]=0; //初始化
scanf("%d",&n); //读入n
for(i=1;i<=n;i++) //循环读入n个图书的ISBN号
{
scanf("%d",&t); //把每一个ISBN号读到变量t中
a[t]=1; //标记出现过的ISBN号
}
for(i=1;i<=1000;i++) //依次判断1~1000这个1000个桶
{
if(a[i]==1)//如果这个ISBN号出现过则打印出来
printf("%d ",i);
}
getchar();getchar();
return 0;
}
这种方法的时间复杂度就是桶排序的时间复杂度,为 O(N+M)。
第二种:
#include
int main()
{
int a[101],n,i,j,t;
scanf("%d",&n);
//读入n
for(i=1;i<=n;i++) //循环读入n个图书ISBN号
{
scanf("%d",&a[i]);
}
//开始冒泡排序
for(i=1;i<=n-1;i++)
{
for(j=1;j<=n-i;j++)
{
if(a[j]>a[j+1])
{ t=a[j]; a[j]=a[j+1]; a[j+1]=t; }
}
}
printf("%d ",a[1]); //输出第1个数
for(i=2;i<=n;i++) //从2循环到n
{
if( a[i] != a[i-1] ) //如果当前这个数是第一次出现则输出
printf("%d ",a[i]);
}
getchar();getchar();
return 0;
}
总结:我们来回顾一下本章三种排序算法的时间复杂度。桶排序是最快的,它的时间复杂度是O(N+M);冒泡排序是 O(N 2 );快速排序是 O(NlogN)。
最后,你可以到“添柴编程学习网”提交本题的代码,来验证一下你的解答是否完全正确。《小哼买书》题目的地址如下:www.tianchai.org/problem-12001.html,接下来,本书中的所有算法都可以去“添柴编程学习网”一一验证。如果你从来没有使用过类似“添柴-编程学习网”这样的在线自动评测系统(online judge).