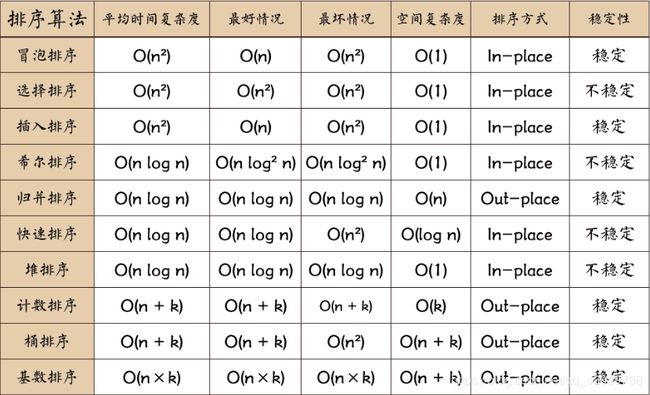
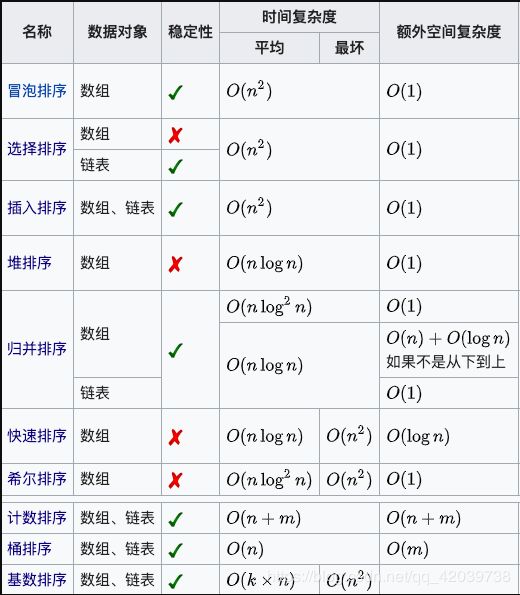
十大基础排序

1、冒泡排序（时间复杂度——O（n^2））

public class BubbleSort {
    public static void main(String[] args) {
        int[] array = randomArray(10, 20);
        System.out.println(Arrays.toString(array));
        int[] sort = bubbleSort(array);
        System.out.println(Arrays.toString(sort));
    }

    public static int[] randomArray(int size, int range) {
        int[] array = new int[size];
        Random random = new Random();
        for (int i = 0; i < array.length; i++) {
            array[i] = random.nextInt(range);
        }
        return array;
    }

    public static int[] bubbleSort(int[] array) {
        //拷贝数组
        int[] copyArray = Arrays.copyOf(array, array.length);
        int length = copyArray.length, temp, count;

        //每趟排序，将最大的数排在后面
        for (int i = 0; i < length - 1; i++) {
            //重置count
            count = 0;
            for (int j = 0; j < length - 1 - i; j++) {
                //如果前面的数比后面的数大，则交换
                if (copyArray[j] > copyArray[j + 1]) {
                    temp = copyArray[j];
                    copyArray[j] = copyArray[j + 1];
                    copyArray[j + 1] = temp;
                    count++;
                }
            }
            //如果该循环交换次数只有等于0的情况下则不用再排了
            if (count == 0) {
                break;
            }
        }
        return copyArray;
    }
}

采用8万个数据测试冒泡排序的性能

public static void main(String[] args) {
        long start, end;
        int[] array = randomArray(80000, 80000);
        start = System.currentTimeMillis();
        int[] sort = bubbleSort(array);
        end = System.currentTimeMillis();
        System.out.println("耗时:" + (end - start));
    }

多次测试平均10秒左右

---

2、选择排序（时间复杂度——O（n^2））

public class SelectSort {
    public static void main(String[] args) {
        int[] array = randomArray(10, 20);
        int[] sort = selectSort(array);
        System.out.println(Arrays.toString(array));
        System.out.println(Arrays.toString(sort));
    }

    public static int[] randomArray(int size, int range) {
        int[] array = new int[size];
        Random random = new Random();
        for (int i = 0; i < array.length; i++) {
            array[i] = random.nextInt(range);
        }
        return array;
    }

    public static int[] selectSort(int[] array){
        int[] copyArray = Arrays.copyOf(array, array.length);
        int length = copyArray.length, min, minIndex = 0;
        for (int i = 0; i < length-1; i++) {
            //每次假定第一个数是最小的
            min = copyArray[i];
            minIndex = i;
            for (int j = i + 1; j < length; j++) {
                //比较，重置最小值
                if(copyArray[j]<min){ //如果按从大到小排序只需修改成大于号
                    min = copyArray[j];
                    minIndex = j;
                }
            }
            //判断最小值是否仍是第一个数，避免不必要的交换
            if(minIndex!=i){
                //交换最小值和第一个数
                copyArray[minIndex] = copyArray[i];
                copyArray[i] = min;
            }
        }
        return copyArray;
    }
}

采用8万个数据测试选择排序的性能

public static void main(String[] args) {
        long start, end;
        int[] array = randomArray(80000, 80000);
        start = System.currentTimeMillis();
        int[] sort = selectSort(array);
        end = System.currentTimeMillis();
        System.out.println("耗时:" + (end - start));
    }

多次测试平均3秒左右

---

3、插入排序 （时间复杂度——O（n^2））

写代码时，前一个元素进行后移的体现是，将前一个元素覆盖后一个元素（插入值已经被存起来）

public class InsertSort {
    public static void main(String[] args) {
        int[] array = randomArray(10, 20);
        System.out.println(Arrays.toString(array));
        int[] sort = insertSort(array);
        System.out.println(Arrays.toString(sort));
    }

    public static int[] randomArray(int size, int range) {
        int[] array = new int[size];
        Random random = new Random();
        for (int i = 0; i < array.length; i++) {
            array[i] = random.nextInt(range);
        }
        return array;
    }

    public static int[] insertSort(int[] array) {
        int[] copyArray = Arrays.copyOf(array, array.length);
        int length = copyArray.length, insertVal, insertIndex;

        for (int i = 0; i < length - 1; i++) {
            insertIndex = i;    //保存插入值的前一个进行比较的元素的下标
            insertVal = copyArray[i + 1];   //保存插入数据的值
            /*
                如果插入值小于前一个元素，则让前一个元素覆盖掉插入元素的位置；往前比较的同时也要注意数组下标的越界问题insertIndex >= 0。以此类推。
                如果插入值大于前一个元素，则不用进行操作。
             */
            while (insertIndex >= 0 && insertVal < copyArray[insertIndex]) {
                copyArray[insertIndex + 1] = copyArray[insertIndex];
                insertIndex--;
            }
            /*
                判断是否要替换元素。
                两种情况：
                第一种：插入值大于前一个元素，即插入原来的位置
                第二种：插入值小于前一个元素，while循环中最后insertIndex每次都自减一次，所以这里必须加一才可以正确表示插入位置
             */
            if (i + 1 != insertIndex + 1) {
                copyArray[insertIndex + 1] = insertVal;
            }
        }
        return copyArray;
    }
}

采用8万个数据测试插入排序的性能

public static void main(String[] args) {
        long start, end;
        int[] array = randomArray(80000, 80000);
        start = System.currentTimeMillis();
        int[] sort = insertSort(array);
        end = System.currentTimeMillis();
        System.out.println("耗时:" + (end - start));
    }

多次测试平均0.6秒左右

---

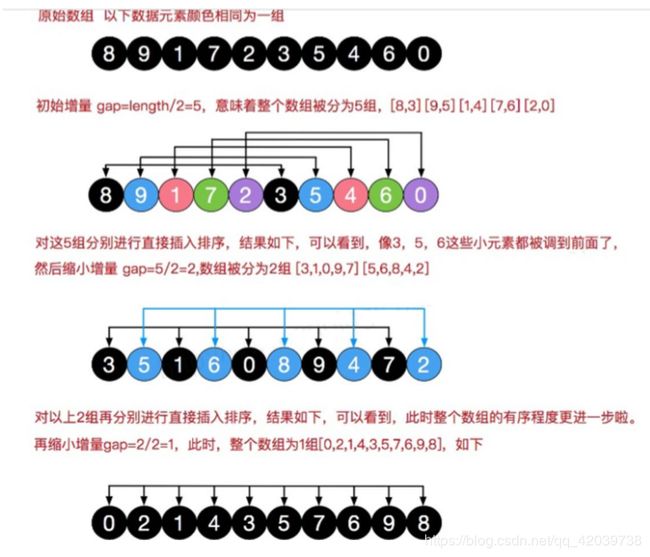
4、希尔排序（插入排序的增强版）（时间复杂度——O（nlogn）

简单概括：

通过步长gap分多个组，每个组进行插入排序。随着gap不断缩小，插入排序最后面向整个数组

注意：

但代码中体现的是同时对所有分组进行插入排序，而不是一个个分组按顺序来操作。它是交叉操作的

public class HillSort {
    public static void main(String[] args) {
        int[] array = randomArray(10, 20);
        int[] sort = hillSort(array);
        System.out.println(Arrays.toString(array));
        System.out.println(Arrays.toString(sort));
    }

    public static int[] randomArray(int size, int range) {
        int[] array = new int[size];
        Random random = new Random();
        for (int i = 0; i < array.length; i++) {
            array[i] = random.nextInt(range);
        }
        return array;
    }

    public static int[] hillSort(int[] array) {
        //拷贝数组
        int[] copyArray = Arrays.copyOf(array, array.length);
        int length = copyArray.length, temp, insertIndex, insertVal;

        for (int gap = length/2; gap > 0; gap/=2) {
            for (int i = gap; i < length; i++) {
                insertIndex = i;
                insertVal = copyArray[i];
                while (insertIndex-gap>=0&&insertVal<copyArray[insertIndex-gap]){
                    copyArray[insertIndex] = copyArray[insertIndex-gap];
                    insertIndex-=gap;
                }
                if(insertIndex!=i){
                    copyArray[insertIndex] = insertVal;
                }
            }

        }
        return copyArray;
    }
}

采用8万个数据测试希尔排序的性能

public static void main(String[] args) {
        long start, end;
        int[] array = randomArray(80000, 80000);
        start = System.currentTimeMillis();
        int[] sort = insertSort(array);
        end = System.currentTimeMillis();
        System.out.println("耗时:" + (end - start));
    }

多次测试平均0.018秒左右

采用8百万个数据测试希尔排序的性能

多次测试平均3秒左右

---

5、快速排序 （时间复杂度——O（nlogn）

其实最后我觉得快排的最重要思想就是根据第一个基准元素，轮流按j->i的顺序去比较，挖坑填坑，

如此循环直到 i == j

public class QuickSort {
    public static void main(String[] args) {
        int[] array = randomArray(10, 20);
//        int[] array = {18, 12, 17, 2, 11, 8, 3, 7, 14, 2};
        System.out.println(Arrays.toString(array));
        int[] sort = quickSort(array, 0, array.length - 1);
        System.out.println(Arrays.toString(sort));
    }

    public static int[] randomArray(int size, int range) {
        int[] array = new int[size];
        Random random = new Random();
        for (int i = 0; i < array.length; i++) {
            array[i] = random.nextInt(range);
        }
        return array;
    }

    public static int[] quickSort(int array[], int l, int r) {
        /*
            1、判断这个序列是否只有一个元素，一个元素就不用再排序了
            2、防止递归传递l,r参数时造成数组越界，比如 quickSort(array, i + 1, r); 当i就是数组最后一个元素时，i+1会越界
         */
        if (l < r) {
            int flagVal = array[l], i = l, j = r;
            //i与j相遇之时就是该分组排序结束之时
            while (i < j) {
                /*
                    进行交换
                 */
                while (i < j && array[j] > flagVal) {
                    j--;
                }
                if (i < j) {
                    array[i++] = array[j];
                }

                while (i < j && array[i] <= flagVal) {
                    i++;
                }
                if (i < j) {
                    array[j--] = array[i];
                }
            }
            //最后把坑补上
            array[i] = flagVal;
            quickSort(array, l, i - 1);
            quickSort(array, i + 1, r);
        }
        return array;
    }
}

采用80000个数据测试快速排序的性能

public static void main(String[] args) {
        long start, end;
        int[] array = randomArray(80000, 80000);
        start = System.currentTimeMillis();
        int[] sort = insertSort(array);
        end = System.currentTimeMillis();
        System.out.println("耗时:" + (end - start));
    }

多次测试平均0.022秒左右

采用8百万个数据测试快速排序的性能

多次测试平均1秒左右

---

6、归并排序（时间复杂度——O（nlogn）

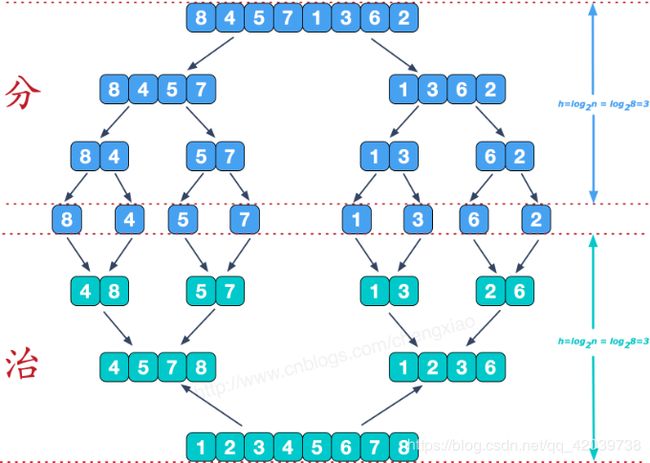
最后一次合并两个有序数组过程

public class MergeSort {
    public static void main(String []args){
        int []arr = {9,8,7,6,5,4,3,2,1};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void sort(int []arr){
        int []temp = new int[arr.length];//在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        sort(arr,0,arr.length-1,temp);
    }
    private static void sort(int[] arr,int left,int right,int []temp){
        if(left<right){
            int mid = (left+right)/2;
            sort(arr,left,mid,temp);//左边归并排序，使得左子序列有序
            sort(arr,mid+1,right,temp);//右边归并排序，使得右子序列有序
            merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
        }
    }
    private static void merge(int[] arr,int left,int mid,int right,int[] temp){
        int i = left;//左序列指针
        int j = mid+1;//右序列指针
        int t = 0;//临时数组指针
        while (i<=mid && j<=right){
            if(arr[i]<=arr[j]){
                temp[t++] = arr[i++];
            }else {
                temp[t++] = arr[j++];
            }
        }
        while(i<=mid){//将左边剩余元素填充进temp中
            temp[t++] = arr[i++];
        }
        while(j<=right){//将右序列剩余元素填充进temp中
            temp[t++] = arr[j++];
        }
        t = 0;
        //将temp中的元素全部拷贝到原数组中
        while(left <= right){
            arr[left++] = temp[t++];
        }
    }
}

采用80000个数据测试归并排序的性能

public static void main(String []args){
        long start, end;
        int[] array = randomArray(80000, 80000);
        start = System.currentTimeMillis();
        sort(array);
        end = System.currentTimeMillis();
        System.out.println("耗时:" + (end - start));
    }

多次测试平均0.018秒左右

性能上是ok的（牺牲了空间换取了性能）

---

7、堆排序（时间复杂度——O（NlogN）

public class HeapSort {
    public static void main(String[] args) throws Exception {
        int[] array = randomArray(10, 20);
        heap_sort(array, array.length);
        System.out.println(Arrays.toString(array));
    }

    public static int[] randomArray(int size, int range) {
        int[] array = new int[size];
        Random random = new Random();
        for (int i = 0; i < array.length; i++) {
            array[i] = random.nextInt(range);
        }
        return array;
    }

    //交换堆顶（最大值）和最后一个节点的值，再进行大顶堆整理
    public static void heap_sort(int tree[], int n) {
        build_heap(tree, n);
        for (int i = n - 1; i > 0; i--) {
            swap(tree, i, 0);
            heapify(tree, i, 0);
        }
    }

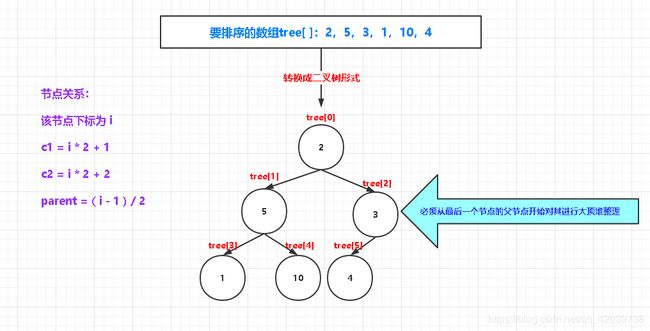
    //构建所有父节点的大顶堆
    public static void build_heap(int[] tree, int n) {
        int lastIndex = n - 1;
        int parent = (lastIndex - 1) / 2;
        for (int i = parent; i >= 0; i--) {
            heapify(tree, n, i);
        }
    }

    /**
     *构建其中一个大顶堆
     * @param tree
     * @param n    数组长度
     * @param i    将要操作的节点下标
     */
    public static void heapify(int[] tree, int n, int i) {
        int c1 = i * 2 + 1;
        int c2 = i * 2 + 2;
        int max = i;

        if (c1 < n && tree[c1] > tree[max]) {
            max = c1;
        }
        if (c2 < n && tree[c2] > tree[max]) {
            max = c2;
        }
        if (max != i) {
            swap(tree, i, max);
            heapify(tree, n, max);
        }
    }

    private static void swap(int[] tree, int i, int max) {
        int temp = tree[i];
        tree[i] = tree[max];
        tree[max] = temp;
    }
}

采用8万个数据测试堆排序的性能

public static void main(String []args){
        long start, end;
        int[] array = randomArray(80000, 80000);
        start = System.currentTimeMillis();
        heap_sort(array, array.length);
        end = System.currentTimeMillis();
        System.out.println("耗时:" + (end - start));
    }

多次测试平均0.018秒左右

采用8百万个数据测试堆排序的性能

多次测试平均2秒左右

---

8、计数排序（时间复杂度——O（N + k）

注意：

该排序只适合数据范围小，量大的数组（排序成绩、年龄是最好的）

计数排序思想简单，但要注意两个点：

1、计数数组的空间优化

2、排序后元素的稳定性

稳定意思是说原本键值一样的元素排序后相对位置不变

稳定性对于简单数据看不出差别，但对于复杂类型就有差别了，比如年龄一样的学生，但不是同一个人

public class CountSort {
    public static void main(String[] args) {
        int[] array = randomArray(10, 10, 20);
        System.out.println(Arrays.toString(array));
        //获取数组值的范围（最大值-最小值）
        Map map = getMaxAndMin(array);
        int[] sort = countSort(array, (Integer) map.get("min"), (Integer) map.get("max"));
        System.out.println(Arrays.toString(sort));
    }

    public static int[] randomArray(int size, int range1, int range2) {
        int[] array = new int[size];
        Random random = new Random();
        for (int i = 0; i < array.length; i++) {
            array[i] = random.nextInt(range2 - range1 + 1) + range1; //注意，这里的元素大小是[range1, range2]
        }
        return array;
    }

    public static int[] countSort(int[] array, int range1, int range2) {
        int size = range2 - range1 + 1;
        int[] countArray = new int[size];
        for (int i = 0; i < array.length; i++) {
            countArray[array[i] - range1]++;
        }
        return copy(countArray, array, range1);
    }

    public static int[] copy(int[] countArray, int[] array, int range1) {
        //新建一个和原始数组一样的数组
        int[] copy = new int[array.length];
        //记录每个元素出现在copy数组出现的最后位置
        for (int i = 1; i < countArray.length; i++) {
            countArray[i] = countArray[i] + countArray[i - 1];
        }
        //根据原始数组从后往前遍历，再根据countArray记录的最后出现的下标，可以保证排序的稳定性
        for (int i = array.length - 1; i >= 0; i--) {
            copy[--countArray[array[i] - range1]] = array[i];
        }
        return copy;
    }

    public static Map getMaxAndMin(int[] array) {
        int max = array[0], min = array[0];
        HashMap<String, Integer> map = new HashMap<>();
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
            if (array[i] < min) {
                min = array[i];
            }
        }
        map.put("max", max);
        map.put("min", min);

        return map;
    }
}

采用8万个数据测试堆排序的性能

public static void main(String[] args) {
        long start, end;
        int[] array = randomArray(80000, 10, 20);
        start = System.currentTimeMillis();
        Map map = getMaxAndMin(array);
        int[] sort = countSort(array, (Integer) map.get("min"), (Integer) map.get("max"));
        end = System.currentTimeMillis();
        System.out.println("耗时:" + (end - start));
    }

多次测试平均0.005秒左右

---

9、基数排序（时间复杂度——O（N + k）

基数排序基本思路：

1、先计算出数组最大值的位数，作为排序的总次数

2、创建二维数组储存排序过程（二维数组使用ArrayList，可动态扩容）

3、第一次循环先排序个位，将按个位排序的结果放到二维数组中，在从二维数组中按顺序取出来，以此

类推

4、最后得到从小到大的数组

public class BasicSort {
    public static void main(String[] args) throws Exception {
        int[] array = randomArray(10, 20);
        System.out.println(Arrays.toString(array));
        //获取数组中值最大值的位数
        int position = countHighestPosition(array);
        basicSort(array, position);
        System.out.println(Arrays.toString(array));
    }

    public static int[] randomArray(int size, int range) {
        int[] array = new int[size];
        Random random = new Random();
        for (int i = 0; i < array.length; i++) {
            array[i] = random.nextInt(range);
        }
        return array;
    }

    private static void basicSort(int[] array, int position) {
        ArrayList<ArrayList> queue = new ArrayList<>(10);
        int x;
        //创建一个二维数组（二维数组适使用ArrayList,可变）
        for (int i = 0; i < 10; i++) {
            queue.add(new ArrayList<>());
        }
        //排的总次数取决于数组最大值的位数
        for (int i = 0; i < position; i++) {
            //先按个位->十位->百位......
            for (int j = 0; j < array.length; j++) {
                x = (int) (array[j]%Math.pow(10, i+1)/Math.pow(10, i));
                queue.get(x).add(array[j]);
            }

            //将二维数组中的元素按顺序取出来放到初始数组中
            int  flag = 0;
            for (int j = 0; j < 10; j++) {
                ArrayList<Integer> q = queue.get(j);
                while (q.size()>0){
                    array[flag++] = q.get(0);
                    q.remove(0);
                }
            }
        }
    }

    public static int countHighestPosition(int[] array){
        int max = array[0], position = 0;
        for (int i = 1; i < array.length; i++) {
            if(array[i]>max){
                max = array[i];
            }
        }
        while (max>0){
            max /= 10;
            position++;
        }
        return position;
    }
}

采用8万个数据测试堆排序的性能

public static void main(String[] args) throws Exception {
        long start, end;
        int[] array = randomArray(80000, 80000);
        start = System.currentTimeMillis();
        //获取数组中值最大值的位数
        int position = countHighestPosition(array);
        basicSort(array, position);
        end = System.currentTimeMillis();
        System.out.println("耗时:" + (end - start));
    }

多次测试平均0.226秒左右

采用8百万个数据测试堆排序的性能

很久，太久了。。。。

---

10、桶排序（时间复杂度——O（N * k）

桶排序的基本思路：

1、找到数组的最小值和最大值，最为该数组的区间范围

2、根据区间范围平均划分，每个区间相当于一个桶。（几个区间随意）

3、将数组元素放进区间桶内

4、对桶中的元素进行排序（采用哪种排序随你）

5、按照桶顺序输出就是从小到大的有序数组