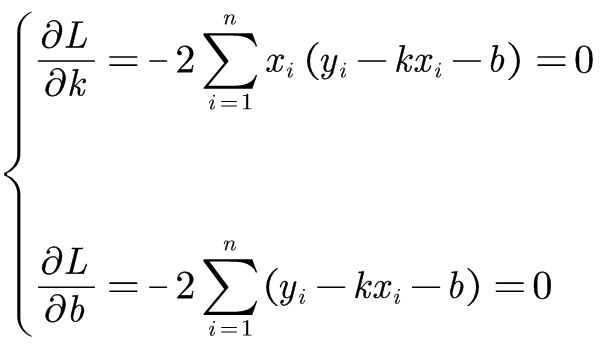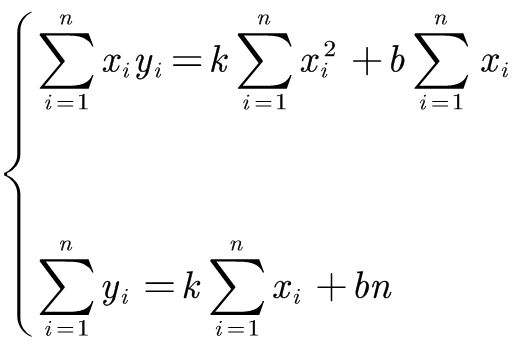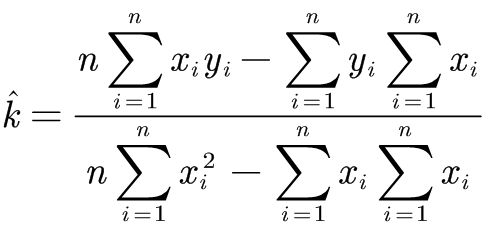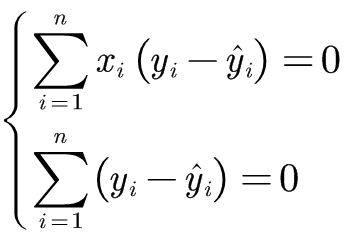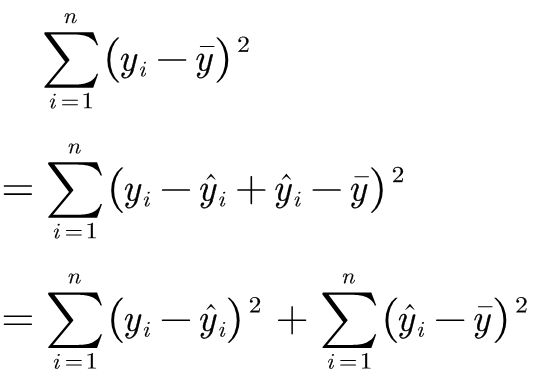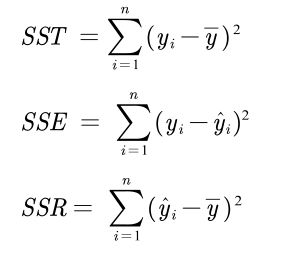MATLAB拟合算法
Preface
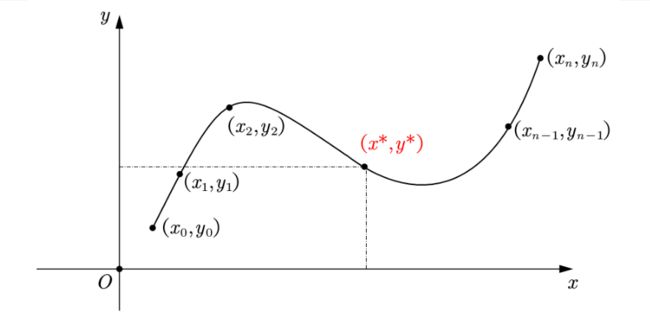
插值算法是要经过所有的点,但当数据很大的时候,如果还要经过所有的样本点,这个时候用于插值的多项式阶数就会非常高,就会出现龙格现象,在样本点附近函数的导数非常大,通常趋于无穷,这就造成了曲线陡峭,波动非常大,此种情况下拟合算法便出现来解决这个问题。
与插值问题不同,在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数(曲线),使得该曲线在某种准则下与所有的数据点最为接近,即曲线拟合的最好(最小化损失函数)。
拟合和插值的区别
插值算法中,得到的多项式 f ( x ) f(x) f(x)要经过所有样本点。但是如果样本点太多,那么这个多项式次数过高,会造成龙格现象。尽管我们可以选择分段的方法避免这种现象,但是更多时候我们更倾向于得到一个确定的曲线,尽管这条曲线不能经过每一个样本点,但只要保证误差足够小即可,这就是拟合的思想。(拟合的结果是得到一个确定的曲线)
一个简单的例子:找出X,Y的最佳拟合曲线
- 先将数据导入 M A T L A B MATLAB MATLAB中
关于如何将 E X C E L EXCEL EXCEL数据导入 M A T L A B MATLAB MATLAB,我上一期已经讲过,请参考博文:将EXCEL数据导入MATLAB
完成如下:
-
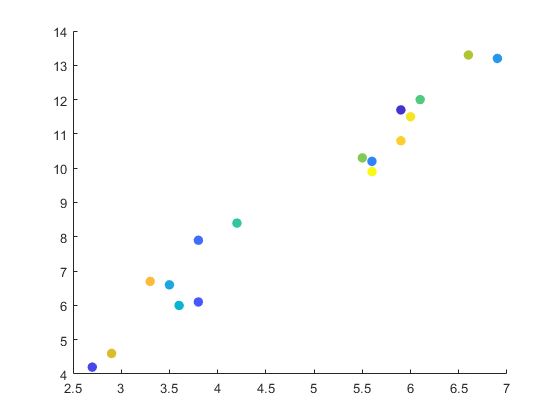
画散点图,查看X和Y的分布趋势
-
以不同的颜色标记散点:要使用不同的颜色,请将
c指定为向量,使用这个有个前提是颜色的数量要与数据的长度保持一致c = linspace(1,10,length(x)); -
用’.'标记数据
scatter(x,y,'.') -
改变标记点大小
>> size = 600; >> scatter(x,y,size,c,'.')
-
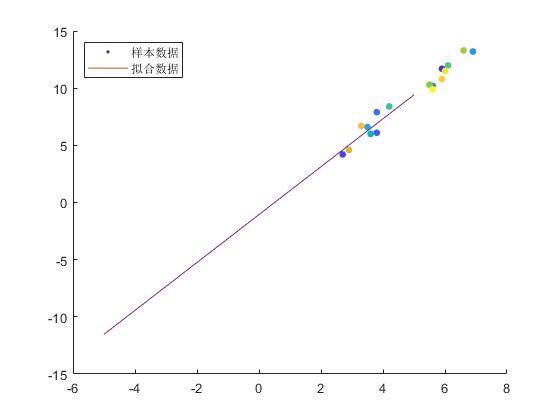
可以看到大致呈直线一次函数关系。
确定拟合曲线
- 我们设这些样本点的坐标为 ( x i , y i ) , i = 1 , 2 , ⋯ , n \left( x_i,y_i \right) ,i=1,2,\cdots ,n (xi,yi),i=1,2,⋯,n
- 我们设置拟合曲线为: y = k x + b y=kx+b y=kx+b
那么问题来了,k和b取何值时样本点和拟合曲线最接近呢?我们先一步一步来,这里要用到最小二乘法的有关知识。
最小二乘法
先介绍最小二乘法的两种定义方式:
- k ∧ , b ∧ = a r g min k , b ( Σ n i = 1 ∣ y i − y ∧ i ∣ ) \overset{\land}{k},\overset{\land}{b}=\underset{k,b}{arg\min}\left( \underset{i=1}{\overset{n}{\varSigma}}\left| y_i-\overset{\land}{y}_i \right| \right) k∧,b∧=k,bargmin(i=1Σn∣∣∣yi−y∧i∣∣∣)
- k ∧ , b ∧ = a r g min k , b ( Σ n i = 1 ( y i − y ∧ i ) 2 ) \overset{\land}{k},\overset{\land}{b}=\underset{k,b}{arg\min}\left( \underset{i=1}{\overset{n}{\varSigma}}\left( y_i-\overset{\land}{y}_i \right) ^2 \right) k∧,b∧=k,bargmin(i=1Σn(yi−y∧i)2)
其中 y ∧ i = k x i + b \overset{\land}{y}_i=kx_i+b y∧i=kxi+b是将x的坐标代入拟合曲线中得到的拟合纵坐标,因为y头上有个三角形的符号,所以我们也叫它y-hat,像戴了一顶帽子一样,arg是参数的英文单词arguement的缩写,以上两种定义方式都是将拟合的纵坐标与实际的纵坐标进行比较,不过第一种是两个直接相减取绝对值,第二个是相减后取平方,而argmin和其下标的意思是,参数(arg)k和b取何值时 y ∧ i , y i \overset{\land}{y}_i\text{,}y_i y∧i,yi的比较值(两种方式)取得最小,也就是用哪一种定义方式可以使得到的误差最小。
使用第二种定义方式
因为不管哪种定义方式,以上得到的肯定是一个函数,既然是一个函数,我们要求它的最小值的话,就必须对其求导,而第一种定义方式含有绝对值,不容易求导,因此计算起来就会比较复杂,而在MATLAB中对高阶的函数求导是十分方便的,所以我们毫不犹豫的选择第二种定义方式,这也是为什么最小二乘法带个二的原因,因为有平方(本人瞎猜的)。
为什么不用四次方?
那肯定就有人要问了,既然MATLAB求解高阶导数比较容易的话,为什么不用三阶,四阶…呢。
- 高阶极端数据对拟和曲线有较大的影响
- 最小二乘法得到的结果与概率论中的 极大似然估计一致
- 奇次方会使误差正负相抵消
况且,我问你,拟合的初衷是什么?难道像插值一样经过每个样本点然后产生龙格现象?拟合就是要用最简单的函数模拟出数据的走势。
求解k,b(过程复杂,可省略)
设这些样本点为 ( x i , y i ) , i = 1 , 2 , ⋯ , n \left( x_i,y_i \right) ,i=1,2,\cdots ,n (xi,yi),i=1,2,⋯,n,我们设置的拟合曲线为 y = k x + b y=kx+b y=kx+b,拟合值等于 y ∧ i = k x i + b \overset{\land}{y}_i=kx_i+b y∧i=kxi+b,那么 k ^ , b ^ = arg min k , b ( ∑ i = 1 n ( y i − y ^ i ) 2 ) = arg min k , b ( ∑ i = 1 n ( y i − k x i − b ) 2 ) \hat{k},\hat{b}=\underset{k,b}{\text{arg}\min}\left( \sum_{i=1}^n{\left( y_i-\hat{y}_i \right) ^2} \right) =\underset{k,b}{\text{arg}\min}\left( \sum_{i=1}^n{\left( y_i-kx_i-b \right) ^2} \right) k^,b^=k,bargmin(i=1∑n(yi−y^i)2)=k,bargmin(i=1∑n(yi−kxi−b)2)
-
令 L = ∑ i = 1 n ( y i − k x i − b ) 2 L=\sum_{i=1}^n{\left( y_i-kx_i-b \right) ^2} L=∑i=1n(yi−kxi−b)2
-
现在要找
k,b使得L最小,最小的k和b就是 k ∧ , b ∧ \overset{\land}{k},\overset{\land}{b} k∧,b∧ -
因为
L的函数中k和b都是变量,所以要求解最小值的话就需要分别对其求偏导。
- 移项
- 变形
k
b
MATLAB求解最小二乘
clear,clc;
load xy;
size = 300;
n = length(x) %求出x矩阵有多少行
c = linspace(1,10,l) %产生一系列颜色,颜色向量c要与数据x的维度一致
scatter(x,y,size,c,'.') %以大小为300,系列可变颜色,标记符号为"."的规则绘制散点图
hold on;
k = (n*sum(x.*y)-sum(y)*sum(x)) / (n*sum(x.^2)-sum(x)*sum(x)) %拟合曲线的斜率
b = (sum(x.^2)*sum(y)-sum(x)*sum(x.*y)) / (n*sum(x.^2)-sum(x)*sum(x)) %拟合曲线的截距
%% 根据已知斜率绘制直线
f = @(x) k*x+b; %求解函数的形式,@符号后面跟上自变量(如果自变量有两个的话,则括号里面也有两个)
fplot(f,[-5,5]) %第一个参数是函数,第二个参数是自变量的范围
legend('样本数据','拟合数据')
如何评价拟合的好坏?
三个指标
- 总体平方和(Total sum of squares)
S S T = ∑ i = 1 n ( y i − y ˉ ) 2 SST=\sum_{i=1}^n{\left( y_i-\bar{y} \right) ^2} SST=i=1∑n(yi−yˉ)2
- 误差平方和(The sum of squares due to error)
S S E = ∑ i = 1 n ( y i − y ^ i ) 2 SSE=\sum_{i=1}^n{\left( y_i-\hat{y}_i \right) ^2} SSE=i=1∑n(yi−y^i)2
- 回归平方和(Sum of squares of the regression)
S S R = ∑ i = 1 n ( y ^ i − y ˉ ) 2 SSR=\sum_{i=1}^n{\left( \hat{y}_i-\bar{y} \right) ^2} SSR=i=1∑n(y^i−yˉ)2
一个等式
S S T = S S E + S S R SST =SSE+SSR SST=SSE+SSR
一个系数
R 2 R^2 R2称为拟合优度,也叫可决优度,是表示拟合好坏的指标, R 2 R^2 R2越接近1,说明误差平方和 S S E SSE SSE越接近0,误差越小说明拟合的越好。
- R 2 R^2 R2只能用于拟合函数是线性函数时对其拟合结果的评价
- 非线性函数和其它函数(例如复杂的指数函数)比较拟合的好坏时,直接看 S S E SSE SSE即可
- R 2 R^2 R2可能为负
证明 S S T = S S E + S S R SST =SSE+SSR SST=SSE+SSR
这里要用到前面的求导的条件
而 y ∧ i = k x i + b \overset{\land}{y}_i=kx_i+b y∧i=kxi+b,带入得到
所以
即
S S T = S S E + S S R SST =SSE+SSR SST=SSE+SSR
何为线性函数?
R 2 R^2 R2只能用于拟合函数是线性函数时,拟合结果的评价
线性函数通常有两个概念,第一个是对参数线性,另一个是对变量线性,我们主要讨论的是对参数线性。
- 线性于参数
- 线性于变量
参考古扎拉蒂《计量经济学基础》
一个易错的点
y = a + b x 2 y=a+bx^2 y=a+bx2是线性函数吗?
a,b都是常数的情况下,y就是一个线性函数,线性于参数。
如何判断线性于参数?
在函数中,参数仅以一次方出现,且不能乘以或除以其他任何的参数,并不能出现参数的复合函数形式。
线性于参数的例子
非线性于参数的例子
MATLAB计算拟合优度
mean()是求均值的函数
y_hat = k*x+b; %y的拟合值
SSR = sum((y_hat-mean(y)).^2) %回归平方和
SSE = sum((y-y_hat).^2) %误差平方和
SST = sum((y-mean(y)).^2) %总体平方和
R_2 = SSR/SST %拟合优度
k =
2.0948
b =
-1.0548
SSR =
151.1583
SSE =
5.7281
SST =
156.8863
R_2 =
0.9635
完整代码
clear,clc;
load xy;
size = 300;
l = length(x) %求出x矩阵有多少行(2表示列)
c = linspace(1,10,l) %产生一系列颜色,颜色向量c要与数据x的维度一致
scatter(x,y,size,c,'.') %以大小为300,系列可变颜色,标记符号为"."的规则绘制散点图
hold on;
k = (l*sum(x.*y)-sum(y)*sum(x)) / (l*sum(x.^2)-sum(x)*sum(x)) %拟合曲线的斜率
b = (sum(x.^2)*sum(y)-sum(x)*sum(x.*y)) / (l*sum(x.^2)-sum(x)*sum(x)) %拟合曲线的截距
%% 根据已知斜率绘制直线
f = @(x) k*x+b; %求解函数的形式,@符号后面跟上自变量(如果自变量有两个的话,则括号里面也有两个)
fplot(f,[-5,5]) %第一个参数是函数,第二个参数是自变量的范围
legend('样本数据','拟合数据')
y_hat = k*x+b; %y的拟合值
SSR = sum((y_hat-mean(y)).^2) %回归平方和
SSE = sum((y-y_hat).^2) %误差平方和
SST = sum((y-mean(y)).^2) %总体平方和
R_2 = SSR/SST %拟合优度
转载请注明出处