布隆过滤器实现及应用

布隆过滤器 BloomFilter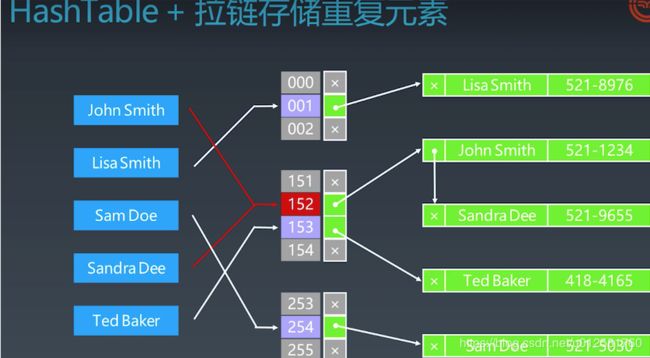

上图为哈希表:哈希表如果有重复元素采用拉链存储法,本身任何一个字符串进来经过一个哈希函数映射到整数下标位置index,比如 Lisa Smith映射到001,就存在001这个位置,她的电话是521-8976, Johe Smith和Sandra Dee都被哈希到152的位置,采用的冲突办法就是在152位置开一个链表,将多个元素存在相同位置的链表处,对于哈希表不仅有哈希函数得到这么一个index值,且会把整个要存的元素,全部放在哈希表中,这是个没有误差的数据结构,有多少个元素,那么这些元素需要占的内存空间,在哈希表中都要找相应的内存大小给存进来,但是在很多时候,我们并不需要存元素本身,而只需要存一个信息就是判断下这个元素到底有没有在这个表中,如果只查询有没有,我们就需要一种更高效的数据结构
更高效的数据结构可以导致一个结果就是有很多元素存的话,但是表本身所需要的内存空间很少,同时不需要把元素本身String名称电话全部都
存下来,只需要说这个东西到底有还是没有,
哈希表可以存很多信息,所以哈希表不只是能判断是否在集合中,同时还可以存元素本身和元素各种额外信息
而布隆过滤器只用来检索一个元素在还是不在集合中这样的信息

Bloom Filter vs Hash Table

一个很长的二进制向量和一系列随机映射函数.布隆过滤器可以用于检索一个元素是否在一个集合中
优点是空间效率和查询时间都远远超过一般的算法(模糊查询)
缺点是有一定的误识别率和删除困难
布隆过滤器示意图

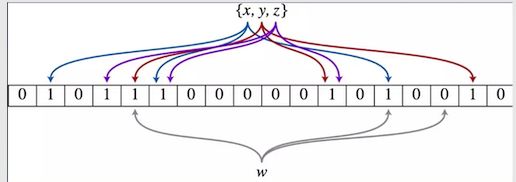
假设要存三个元素依次存进去,每一个元素会分配到一系列二进制位中,假设x就被分配到3个二进制位(蓝色线)中, 把x插入到布隆过滤器就是把x对应的三个位置置为1,同理依次存入y,z,这里这个二进制数组用来表示所有已经存入的xyz是否在索引中
这时候有个w中有1个0位说明,w未在索引中,如果一个元素所对应的二进制位,只要有1个为0就说明这个元素不在布隆过滤器的索引中且可以肯定不在,但是如果重新元素d对应都二进制位都为1,我们也不一定说元素一定在索引中

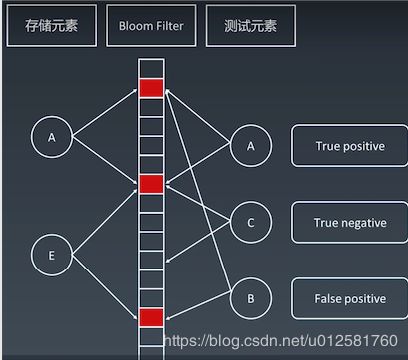
结论:当布隆过滤器把元素全部都插入完了之后,对于测试元素来验证它是否存在也就是它对应的二进制位都为1的时候,我们只能说可能
存在布隆过滤器里面
在布隆过滤器中查,如果不在,肯定不在,如果在,不一样存在
布隆过滤器只是挡在一台机器前面的快速查询的缓存,真正要确定测试元素一定存在的话,必须再访问这个机器
里面的一个完整的存储数据结构,一般来说就是数据库

案例

1 比特币网络
(比特币是分布式系统,在分布式系统中,一个地址是否在这个节点里或者transaction是否在node中经常用到布隆过滤器进行快速查询)
2 分布式系统(Map-Reduce) Hadoop search engine之类的东西
比如搜索引擎做的事情就是把大量的网页信息,还有图片信息都存在整个服务器里面,一般来说
不同网页是存在不同的集群中,当search时,查到一个东西之后,就会根据索引,知道应该在那个集群
就先在集群布隆过滤器中查询看是否存在,如果存在就再去集群的DB里面进行访问,如果不存在直接过滤
所以在大型分布系统中,很多人使用布隆过滤器同时的话,Redis缓存以及垃圾邮件或者一个评论它到底是不是
涉黑 的不正当言论用布隆过滤器很快判断不是的话,肯定不是,是的话再去DB中查
布隆过滤器实现原理
使用布隆过滤器解决缓存击穿、垃圾邮件识别、集合判重
布隆过滤器 Python 实现示例
高性能布隆过滤器 Python 实现示例
布隆过滤器 Java 实现示例 1
布隆过滤器 Java 实现示例 2

# Python  布隆过滤器
from bitarray import bitarray  #bitarray系统的数据结构就是一个数组,数组中都存的二进制位
import mmh3 
class BloomFilter: 
	def __init__(self, size, hash_num): 
		self.size = size  #总共有多少个元素,hash_num指一个元素进来分成多少个二进制位存储
		self.hash_num = hash_num 
		self.bit_array = bitarray(size) 
		self.bit_array.setall(0) #将二进制位数组索引全部都为0, 
	def add(self, s): 
		for seed in range(self.hash_num): 
		 # 循环hash_num次,假设hash_num为3就生成3个二进制位,每次将seed和元素s进行一次hash再模上bitarray的size,因为不能让下标超出去
			result = mmh3.hash(s, seed) % self.size 
			self.bit_array[result] = 1  #把相应的二进制位的索引处置为1
	def lookup(self, s): 
		for seed in range(self.hash_num): 
			result = mmh3.hash(s, seed) % self.size 
			if self.bit_array[result] == 0: #只要下标result为0就确定肯定不存在
				return "Nope" 
		return "Probably" # 全部都为1,输出可能
bf = BloomFilter(500000, 7) 
bf.add("dantezhao") 
print (bf.lookup("dantezhao")) 
print (bf.lookup("yyj")) 

//Java
public class BloomFilter {
    private static final int DEFAULT_SIZE = 2 << 24;
    private static final int[] seeds = new int[] { 5, 7, 11, 13, 31, 37, 61 };
    private BitSet bits = new BitSet(DEFAULT_SIZE);
    private SimpleHash[] func = new SimpleHash[seeds.length];
    public BloomFilter() {
        for (int i = 0; i < seeds.length; i++) {
            func[i] = new SimpleHash(DEFAULT_SIZE, seeds[i]);
        }
    }
    public void add(String value) {
        for (SimpleHash f : func) {
            bits.set(f.hash(value), true);
        }
    }
    public boolean contains(String value) {
        if (value == null) {
            return false;
        }
        boolean ret = true;
        for (SimpleHash f : func) {
            ret = ret && bits.get(f.hash(value));
        }
        return ret;
    }
    // 内部类，simpleHash
    public static class SimpleHash {
        private int cap;
        private int seed;
        public SimpleHash(int cap, int seed) {
            this.cap = cap;
            this.seed = seed;
        }
        public int hash(String value) {
            int result = 0;
            int len = value.length();
            for (int i = 0; i < len; i++) {
                result = seed * result + value.charAt(i);
            }
            return (cap - 1) & result;
        }
    }
}