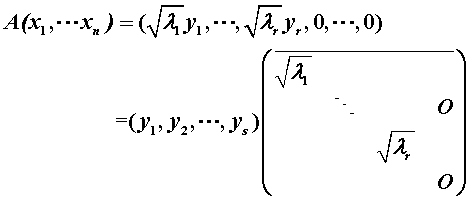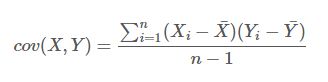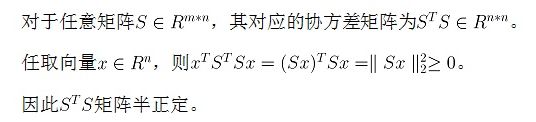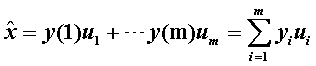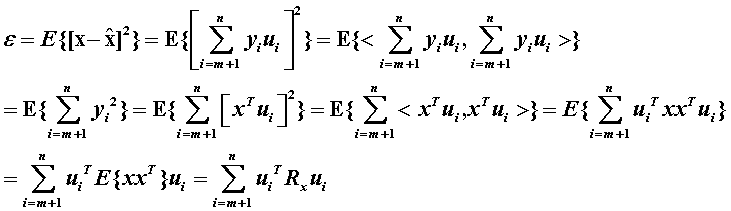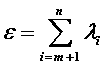彻底理解PCA（Principal Component Analysis）主成分分析

理解矩阵特征值、特征向量

 

对于一个矩阵A，它的特征值和特征向量代表着什么？

矩阵代表着一个线性变换，包括旋转和伸缩。旋转和伸缩的是向量所在坐标系的基。

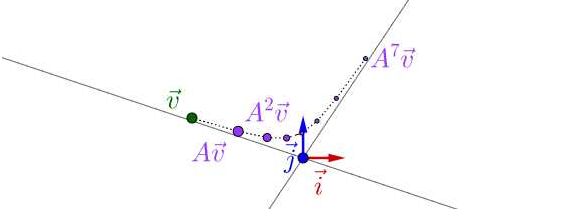
如果一个向量在A作用后没有发生旋转，只是大小发生了变化，那么这个向量就是A的特征向量，变化的倍数就是对应的特征值，特征值的正负代表变化的方向。可以直观的看出，特征向量方向上的所有向量都是对应于这个特征值的特征向量。所有特征向量组成的空间叫做特征空间。现在我们知道特征值可以表征特征向量指向的方向上的向量经A作用后伸缩的速度，其他方向上的变化可以用这几个特征向量的变化合成。

一个直观的例子是：如果你用A持续作用在这个向量上，最终向最大特征值所在方向靠拢，因为这个方向上变化最快，所占的比例会越来越大。

 

 

 

如果A是正定矩阵，可以进行对角化：

分解之后的P代表A的旋转作用，Λ代表A的伸缩作用。P的列向量是单位正交的，这时特征向量就变成了刻画向量的基。

旋转是将特征向量旋转到标准基的位置，伸缩是伸缩各对应方向的基。其他方向的伸缩可以由变化后的基合成得到。乘以P的逆再把基旋转回原来的位置。

可以参考知乎回答：

https://www.zhihu.com/question/20507061/answer/120540926

https://www.zhihu.com/question/21874816/answer/181864044

 

 

如果A是半正定的，则可以进行奇异值分解（Singular Value Decomposition，SVD）：

 

 

其中是一个对角阵，主对角元素均大于或等于0。

 

假设A是秩为r 的s x n 矩阵，是秩为r 的半正定矩阵。设其非零特征值为，令，，则一定存在s阶酉矩阵U和n阶酉矩阵V，使得

。

证明如下：

假设的特征值为，相应的标准正交特征向量组是，即

。

所以，

因此，是一正交向量组，并且

。

令

则是中的一标准正交向量组，将之扩充成的标准正交基：，

则有

于是，若令

，

则U,V都是酉矩阵，且

 

 

 

理解协方差矩阵

先谈谈方差定义，

或者写作D(X)=E{[X-E(X)]^2}

方差是样本与均值之差的平方和的平均值，刻画了随机变量的取值与其数学期望的离散程度。这里之所以除以n-1 而不是 n ,是因为各样本与均值并不是完全独立的，除以n得到的是方差的一致估计，除以n-1 得到的是方差的无偏估计。

两个随机变量X，Y的协方差定义为：

或者写作COV(X，Y)=E[(X-E(X))(Y-E(Y))] 

协方差反映的是两个变量总体误差的方差。如果两个变量变化趋势一致，值为正；变化趋势相反，值为负，即我们所说的变量之间的相关性，为0则不相关。相关指的是两个变量之间的线性关系。

由定义我们可以得到协方差的两个重要性质：

如果你收集的样本是n 维的，有m 个这样的样本，那么各个维度的样本值之间的协方差组成的矩阵就是协方差矩阵：

其中是m x 1 的向量。得到的协方差矩阵是一个n x n 的矩阵，矩阵中的每一个值反映的是维度之间的相关性。

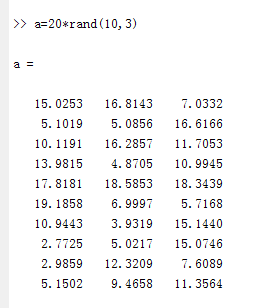
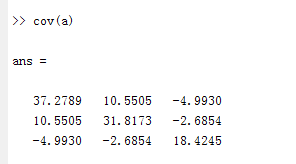
举一个三维样本的例子：

比如说计算第一维和第二维的协方差：

mean(X1)=10.3085;

mean(X2)=9.9381;

cov(X1,X2)=[（第一列各值 - 第一列均值）点乘（第二列各值 - 第二列均值） ]  /  （样本个数 - 1）

                  =[ (15.0253-10.3085)*(16.8143-9.9381)+(5.1019-10.3085)*(5.0856-9.9381)+(10.1191-10.3085)*(16.2857-9.9381)+(13.9815-10.3085)*(4.8705-9.9381)+(17.8181- 10.3085)*(18.5853-9.9381)+(19.1858-10.3085)*(6.9997-9.9381)+(10.9443-10.3085)*(3.9319-9.9381)+(2.7725-10.3085)*(5.0217-9.9381)+(2.9858-10.3085)*(12.3209-9.9381)+(5.1502-10.3085)*(9.4658-9.9381) ]  /  9

                 =  10.5505

matlab验证：

用cov函数求解协方差矩阵：

 

协方差矩阵是对称阵，它还有一个重要的性质，就是协方差矩阵是半正定阵，证明如下：

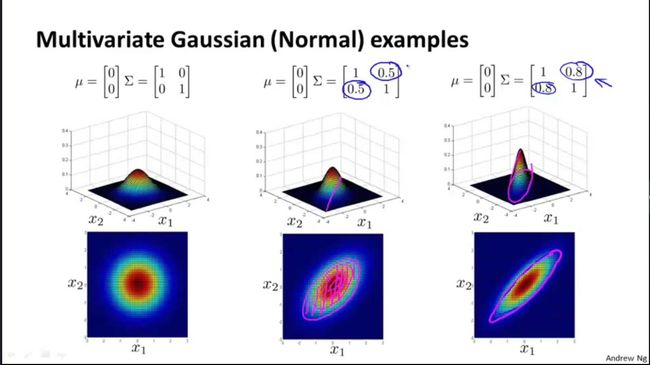
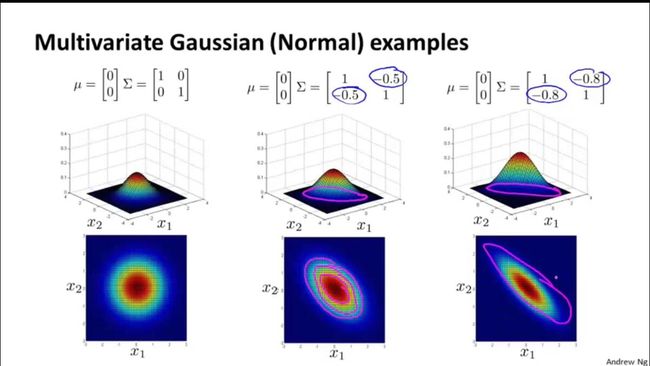
最后，我们用多维高斯函数来看下不同协方差的数据分布是怎样的：

 

 

 

从K-L变换说起

 

设X,Y为两个Hilbert空间，x，y分别是其中的向量，对于线性变换y=Ax，若A将x变换为y后，其范数保持不变，即

，则称A是正交变换。

正交变换的好处：

1.是线性变换；

2.反变换唯一存在：;

3.正交变换的正反变换用硬件容易实现，不需要求逆了；

4.利用正交变换可以把实对称矩阵对角化，如果这个实对称矩阵是数据的协方差矩阵意味着数据之间的去相关，便于数据压缩。

Karhunen-Loeve Transform是一种特殊的正交变换：对于给定的随机向量，经K-L变换后变为n 点随机向量y  ,y的各分量之间完全去除了相关性，且y对x截断近似好时，均方误差最小。

K-L变换的思想即是寻求正交矩阵U，使得U对x的变换的自协方差矩阵为对角阵。（去除了各维度之间的相关性）

步骤如下：

1.由特征多项式求矩阵Rx 的特征值；

2.由求Rx 的特征向量（已经相互正交）；

3.将归一化；

4.将归一化后的构成归一化正交矩阵U；

5.由实现对信号x 的K-L变换。

此时，。

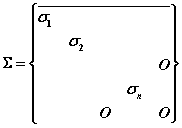
y的协方差矩阵Ry 成了对角阵：

 

 

 

我们可以把K-L变换看成对向量x 作基是的展开：

实际上x可以在空间的任意一组基上展开，如果希望对x 截断达到降维或做数据压缩，（即舍去yn中的一部分分量），怎样才是最有截断呢？

我们假设是任意一组正交归一化基矢量，取展开式m项（m

对近似的均方误差是：

现在要在归一化正交的约束下，设计，使得阶截断误差最小，因此使用Lagrange条件极值法：

得到

即

说明基向量应选的特征向量。

将上式代入的表达式可以得到

所以为了使截断误差最小，应将按的降序排列，这时得到的最小：

因此，K-L变换也可以解释为：给定随机信号向量x，寻求一组基向量使得在相应的变换域对x截断后均方误差最小。

 

K-L变换的缺点：
1.每一个数据序列都需要自己的K-L变换基矢量；

2.计算量大；

3.没有快速算法。

 

PCA算法

K-L变换的一个具体应用就是主分量分析（PCA）。主成分分析的原理就是将一个高维向量x,通过一个特殊的特征向量矩阵U，投影到一个低维的向量空间中，用一个低维向量y表示，并且损失的信息最少或者说仅仅损失了一些次要信息。PCA将大量具有相关性的数据变换为一个不相关的特征分量集合，集合中的分量按信息内容量降序排列。

 

总结一下PCA的算法步骤：

设有m个 n维数据（这里一行代表一个样本，具体看数据怎么排列数据）

1.将原始数据按列组成m行n列矩阵X

2.将X进行零均值化，即减去这一列的均值

3.求出协方差矩阵

4.求出协方差矩阵的特征值及对应的特征向量

5.将特征值从大到小排列，将特征向量按特征值顺序组成一个矩阵，取前k个特征矢量组成矩阵U

6.Y=UTX即为降为k维的新数据。

 

分析1:

 

由可得，其中。又，可得，前面已证明，所以。

所以降维后的数据y 各分量被去相关，且各分量yi 的反差是λi 。

分析2：

前面我们已经证明了，是的线性最小均方误差（LMMSE）估计。估计误差是

分析3：
PCA可以与数据矩阵X的SVD相联系。假设X是MxN的矩阵(M>N)，则X可以分解为：，分别是MxM,NxN 的正交归一化矩阵，是MxN的矩阵，其中。

分析4：
对各yi 的几何意义，比如分量 ，，其方差，

所以，第一主分量的方向是沿着具有最大方差的特征矢量方向。类似，的方向是沿着与相正交的另一最大方差方向。

分析5：

实际中多采用迭代学习的方法实现PCA，因为协方差和矩阵正交分解的计算量巨大，且当有新样本假如是时协方差矩阵必须重新估计。

 

PCA的迭代算法

最小化某目标函数来设计，主要要考虑收敛速度和步长的选择。这里只给出几种优化方法：

1.梯度下降和最速下降法；

2.共轭梯度法；

3.牛顿法；

4.递归最小二乘法。

 

 

Matlab自带函数实现：

原始数据：

63 22 28 14 41 78 11 50 84 28
36 37 25 22 60 69 18 43 32 23
100 9 45 18 75 1 10 100 55 71
22 64 23 4 58 84 49 81 98 62
65 18 80 11 55 92 19 49 55 59
60 5 99 62 58 77 90 89 33 66
39 72 3 94 51 4 10 14 62 5
14 35 54 35 8 38 4 39 36 35
3 66 9 41 72 70 56 93 76 45
42 38 80 98 100 73 77 92 41 24
18 63 99 95 35 22 31 71 49 72
73 2 7 68 97 27 18 62 69 86
37 91 94 99 35 67 34 34 97 28
84 80 2 77 89 48 21 94 33 73
73 75 68 34 45 62 51 12 84 14
57 81 78 66 41 24 91 73 74 84
18 38 53 24 22 18 63 65 95 14
96 62 89 30 13 83 10 83 3 59
27 58 90 68 31 77 39 40 36 37
92 53 63 53 73 93 5 75 66 81

data=load('1.txt');
[coeff, score, latent] = pca(data);%coeff特征向量矩阵；score变换后的数据；latent特征值列向量
%  cumsum(latent)./sum(latent) %查看降维后精度
data_1=score(:,1:7);%降到7维，保存88.5%的信息

 

 

特征值降序：
1823.23043228550
1615.80225259831
1335.12264514534
1014.33280039605
754.988410086299
595.638979084022
515.196392534525
318.636202360173
152.888054964567
70.2901463346949
 

降维后数据：

19 -41 -49 11 7 3 -18
9 -36 -32-210-38 6
83 -8 7-18-5220-9
9 -28 -15681822 25
25 19 -5953-3 -18
12 79 329-23-27-20
-40 -80 41 -53 5 -12 -10
-28 -28 -38 -27 -34 -24 27
-1 -32 25 60 20-1433
-9 49 472417-48 -26
-41 36 35 -27 -30 1 25
69 -31 43 -11 -13 -6 -28
-77 13 12 -15 30 25 -17
55 -10 54 -24 38 4 28
-40 -15 -28 -3 20 31 -39
-24 37 44 16 -22489
-40 -34 -7 37 -5210-4
22 55 -54-4488 35
-48 28 -19 -14 8 -22 6
45 27 -10-134123 -6
 

mean=mean(data,1);
mean_2=mean*coeff(:,1:7);
data_2=bsxfun(@plus,data_1,mean_2(:,1:7));

 

加上均值后：

39 57 10 52 7971-42
29 62 27408230 -18
103 90 66 24 2088-33
29 70 441109090 2
45 117 0 47 7565-41
32 177 62 71 4942-43
-20 19 100 -11 78 56 -34
-8 70 22143844 3
19 66 841029254 10
11 147 106 66 90 20 -49
-21 134 95 15 43701
89 67 102315962 -52
-57 111 71 26 10293-41
75 89 1141811172 5
-20 83 32 39 9299-62
-4 135 103 58 50 116 -15
-20 64 52 79 2078-27
42 153 5 -2 807612
-28 126 40 28 8146-17
65 125 49 28 11391-30