数学建模列题整理2
微分方程组的数值模拟
例:某湖泊中有机物新城代谢系统模型的状态方程组
时间 t 是以年为单位,Xs 表示 t 时刻太阳提供的能量,Xp 表示 t 时刻植物生长的数 量,Xh 表示吞食植物的虫类生成数量;Xr 为 t 时刻食虫植物的生长数量;Xo 表示 t 时 刻湖底有机物的沉淀量;Xe 表示 t 时刻已扩散到周围环境的总能量。使用 Matlab 的 ode 命令求解并模拟 1900 年到 2020 年该湖泊每隔 10 年有机物新城代谢情况,Matlab 程序 如下所示:
%微分方程组求解主程序
clc;clear all;clf;close all;
%Windows 时钟自动计时
T1=clock;%Clock 函数返回的值是 clock = [year month day hour minute seconds] disp('计算机正在准备输出湖泊有机物新陈代谢结果,请耐心等待……'); [tt,y]=ode45('lbwfun',[0:10:2020],[95.9,0.83,0.003,0.0001,0.0,0.0]);
t=tt(191:end,:)
ys=y(191:end,1)
yp=y(191:end,2)
yh=y(191:end,3)
yr=y(191:end,4)
yo=y(191:end,5)
ye=y(191:end,6)
T2=clock;
API_elapsed_time=T2-T1;
if API_elapsed_time(6)<0
API_elapsed_time(6)=API_elapsed_time(6)+60;
API_elapsed_time(5)=API_elapsed_time(5)-1;
end
if API_elapsed_time(5)<0
API_elapsed_time(5)=API_elapsed_time(5)+60;
API_elapsed_time(4)=API_elapsed_time(4)-1;
end
str=sprintf('湖泊新陈代谢模拟程序共运行 %d 小时 %d 分钟 %.4f 秒
API_elapsed_time(4),API_elapsed_time(5),API_elapsed_time(6));
disp(str);
微分方程组的子函数: function ydot=lbwfun(t,y);
ydot=[121.793*pi*cos(2*pi*t);
y(1)-4.03*y(2);
0.48*y(2)-17.87*y(3);
4.85*y(3)-4.65*y(4);
2.55*y(2)+6.12*y(3)+1.95*y(4);
1.10*y(2)+6.90*y(3)+2.70*y(4)];
end
服从概率分布的随机模拟
例:
1、模型假设:
(1)顾客到达收银台的时间间隔服从负指数分布;
(2)收银系统连续工作性能仍然稳定;
(3)超市的所有收银台均是相互独立的,各个收银台之间不会因为忙碌的程度不 同导致顾客的流动,即外界环境对收银台没有扰动。
2、模型组建 以超市的某一收银台为研究对象,顾客到达收银台的时间间隔服从平均时间为 10s 的负指数分布,分布函数为:
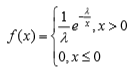
每个顾客的服务时间服从均值为 6.5s,标准差为 1.2s 的正态分布,使用计算机模拟 顾客在收银台的平均逗留时间和收银系统的服务强度(服务占总时间的比率)。
设第 i 个人到达时刻为 ai,开始接受服务的时刻为 bi,离开时刻为 ci,设总共考虑 n 个顾客,n 个顾客到达的时间间隔为服从均值为 10s 的负指数分布序列{dt(n)},每个人接受服务的时间服从正态分布 N(6.5,1.2*1.2)的序列{st(n)},每个人的到达时刻计算公 式为:
a1=0,ai=ai-1+dti-1,i=2,3,…,n
第一个顾客接受服务的时刻为 b1=0,第 1 个顾客离开的时刻为c1=st1,第 i 个顾客开 始接受服务的时刻为:
![]() 说明当第 i 个顾客到达时间比第 i-1 个顾客离开时间早,则开始 接受服务的时间为第 i-1 个顾客离开的时间;当第 i 个顾客到达时间比第 i-1 个顾客离开 的时间完,则开始接受服务的时间就是到达时间,第 i 个顾客离开的时间为:
说明当第 i 个顾客到达时间比第 i-1 个顾客离开时间早,则开始 接受服务的时间为第 i-1 个顾客离开的时间;当第 i 个顾客到达时间比第 i-1 个顾客离开 的时间完,则开始接受服务的时间就是到达时间,第 i 个顾客离开的时间为:
ci=bi+sti,i=2,3,…,n
每个人在收银台的逗留时间为 wti=ci-ai,i=2,3,…,n,到第 n 个人离开时刻为 T=c, 则系统的工作强度占总时间的比值为:
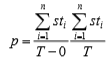
3、模型求解,分别计算 n=10,100,500 等 10 种不同的情况,模拟收银系统的工作强 度和顾客平均逗留时间,每种情况都模拟100次以便尽量减少随机因素,程序如下所示:
clc;close all;clear all;
disp('计算机大概需要两分钟的运行时间,请等待……');
p=zeros(10,100);
avert=zeros(10,100); %分别在顾客人数为 10、100、500 等情况时,模拟系统工作强度和顾客平均逗留 时间
nn=[10 100 500 1000 5000 10000 20000 50000 100000 500000];
for d=1:10 %length(nn)=10
for s=1:100 %每种情况重复模拟 100 次以便消除随机因素
n=nn(d);%模拟顾客数目
dt=exprnd(10,1,n);%到达时间间隔
st=normrnd(6.5,1.2,1,n);%服务台服务时间
a=zeros(1,n);%每个顾客到达时刻
b=zeros(1,n);%每个顾客开始接受服务时刻
c=zeros(1,n);%每个顾客离开时刻
a(1)=0;
for i=2:n
a(i)=a(i-1)+dt(i-1);%第 i 顾客到达时刻
end
b(1)=0;%第一个顾客开始接受服务的时刻是其到达的时刻
c(1)=b(1)+st(1);%第一个顾客的离开时刻为其接受的服务时间加上开始接 受服务的时刻
for i=2:n %如果第 i 个顾客到达时间比前一个顾客离开时间早,则接受服务时间为前一人离 开时间
if(a(i)<=c(i-1))b(i)=c(i-1); %如果第 i 个顾客到达时间比前一个顾客离开时间晚,则接受服务时间为其到达时 间
else b(i)=a(i);
end %第 i 个顾客离开时间为其开始接受服务的时刻+接受服务的时间长度
c(i)=b(i)+st(i);
end
cost=zeros(1,n);%记录每个顾客在系统逗留时间
for i=1:n
cost(i)=c(i)-a(i);%第 i 个顾客在系统逗留时间
end
T=c(n);%总时间
p(d,s)=sum(st)/T;
avert(d,s)=sum(cost)/n;
end
end
pc=sum(p')/100;avertc=sum(avert')/100;
figure(1);
subplot(2,1,1);%分区画图
plot(pc,'color','g','linestyle','-','linewidth',2.5,'marker','*','markersize',5);
text(1,pc(:,1),texlabel('10 人'),'fontsize',11);
text(2,pc(:,2),texlabel('10^2 人'),'fontsize',11);
text(3-0.15,pc(:,3)-0.004,texlabel('5x10^2 人'),'fontsize',11);
text(4-0.15,pc(:,4)-0.004,texlabel('10^3 人'),'fontsize',11);
text(5-0.15,pc(:,5)-0.004,texlabel('5x10^3 人'),'fontsize',11);
text(6-0.15,pc(:,6)-0.004,texlabel('10^4 人'),'fontsize',11);
text(7-0.15,pc(:,7)-0.004,texlabel('2x10^4 人'),'fontsize',11);
text(8-0.15,pc(:,8)-0.004,texlabel('5x10^4 人'),'fontsize',11);
text(9-0.15,pc(:,9)-0.004,texlabel('10^5 人'),'fontsize',11);
text(10-0.15,pc(:,10)-0.004,texlabel('5x10^5 人'),'fontsize',11);
xlim([1 11]);xlabel('顾客数量/个','fontsize',11);ylabel('系统工作强度','fontsize',11); subplot(2,1,2); plot(avertc,'color','r','linestyle','-','linewidth',2.5,'marker','s','markersize',5);
text(1,avertc(:,1)+0.4,texlabel('10 人'),'fontsize',11);
text(2-0.15,avertc(:,2)-0.4,texlabel('10^2 人'),'fontsize',11);
text(3-0.15,avertc(:,3)-0.4,texlabel('5x10^2 人'),'fontsize',11);
text(4-0.15,avertc(:,4)-0.4,texlabel('10^3 人'),'fontsize',11);
text(5-0.15,avertc(:,5)-0.4,texlabel('5x10^3 人'),'fontsize',11);
text(6-0.15,avertc(:,6)-0.4,texlabel('10^4 人'),'fontsize',11);
text(7-0.15,avertc(:,7)-0.4,texlabel('2x10^4 人'),'fontsize',11);
text(8-0.15,avertc(:,8)-0.4,texlabel('5x10^4 人'),'fontsize',11);
text(9-0.15,avertc(:,9)-0.4,texlabel('10^5 人'),'fontsize',11);
text(10-0.15,avertc(:,10)-0.4,texlabel('5x10^5 人'),'fontsize',11); xlim([1 11]);xlabel('顾客数量/个','fontsize',11);ylabel('顾客逗留时间/秒','fontsize',11);
xlim([1 11]);xlabel('顾客数量/个','fontsize',11);ylabel('顾客逗留时间/秒','fontsize',11);