计算机组成原理
计算机发展史(四个阶段)
第一阶段(1946~1957):电子管计算机
世界上第一台计算机叫埃尼阿克(ENIAC)

第二次世界大战是电子管计算机产生的催化剂(英国为了解密德国海军的密文),在第二次世界大战中,战争使用了飞机和火箭,打得准需要计算设计参数,设计参数需要几千次运算才能计算出来,在没有计算机之前 ,这些都需要人工手动去计算,埃尼阿克的计算速度大约是手工计算的20万倍。
埃尼阿克(ENIAC)由18000多个电子管,运行耗电量达150千瓦,重量达30吨,占地1500平方英尺。由此可见,第一阶段的电子管计算机,集成度小,空间占用大,功耗高,运行速度慢,操作复杂,更换程序需要接线。
第二阶段(1957~1964):晶体管计算机
贝尔实验室的三个科学家发明了晶体管,第一台晶体管计算机产生于麻省理工大学的林肯实验室。

第三阶段(1964~1980):集成电路计算机
德州仪器的工程师发明了集成电路(IC),后面就有了集成电路计算机,集成电路计算机让计算机具备进入千家万户的条件。因为集成电路使计算机变得更小,功耗变得更低,计算速度变得更快。

关于集成电路计算机,IBM当时主要推出了两款计算机,使用量比较大,分别是7094和1401,但这两款计算机的主打功能不同,而且相互无法兼容,公司也不愿意投入两组人力,于时后来IBM推出了兼容的产品System/360,这也是操作系统的雏形。
第四阶段(1980~至今):超大规模集成电路计算机

超大规模集成电路,一个芯片上集成了上百万的晶体管,这样使超大规模集成电路计算机速度更快,价格更低,体积更小,更能被大众所接受,而且用途丰富,可以用作文本处理,表格处理,高交互的由于与应用等。
计算机的分类
超级计算机
功能最强、运算速度最快、存储容量最大的计算机,多用于国家高科技领域和尖端技术研究。
运算速度单位是TFlop/s,1TFlob/s=每秒一万亿次浮点数计算
大型计算机
大型计算机又称大型机、大型主机、主机等;具有高性能,可处理大数据与复杂的运算;在大型机市场领域,IBM占据着很大的份额。

去"IOE"行动,"IOE"是分别指IBM,Oracle,EMC,去"IOE"是阿里巴巴提出的概念,代表了高维护费用的存储系统,不够灵活,伸缩性弱。阿里巴巴在2008年提出去“IOE”行动,在2009年成立了阿里云。
迷你计算机(服务器)
迷你计算机也称为小型机,即普通服务器,不需要特殊的空调场所,具备不错的算力,可以完成较复杂的运算。普通的服务器已经替代了传统的大型机,成为大规模企业计算的中枢。
工作站
高端的通用微型计算机,提供比个人计算机更强大的性能,类似于普通台式电脑,体积较大,但性能较强。

微型计算机
微型计算机又称为个人计算机,是最普通的一类计算机。麻雀虽小,五脏俱全,从构成的体质上来讲,个人计算机与前面的分类的无异。

计算机的体系与结构
冯诺依曼体系
冯诺依曼体系:将程序指令和数据一起存储的计算机设计概念结构。在冯诺依曼体系出现前,早期的计算机仅含固定用途程序,如改变程序就需要更改结构,重新设计电路,也就是不能先打会儿游戏然后再写会儿代码,这样就很影响我们的使用体验,所以就提出将程序存储起来,并设计成通用电路,即存储程序指令,设计通用电路。
冯诺依曼体系提出:计算机必须有一个存储器、有一个控制器、有一个计算器、有输入设备和输出设备。这样就能够把需要的程序和数据送至计算机中(输入设备),能够长期记忆程序、数据、中间结果及最终运算结果的能力(存储器),能够具备算术、逻辑运算和数据传送等数据加工处理的能力(运算器、控制器),能够按照要求将处理结果输出给用户(输出设备)。

由于CPU处理数据的速度要远快于存储器的存储速度,所以CPU和存储器的分开会造成芬诺伊曼瓶颈,也就是CPU和存储器之间的速率问题无法调和。

现代计算机的结构
现代计算机在冯诺曼体系结构基础上进行修改,解决CPU与存储设备之间的性能差异问题。

计算机的层次与编程语言
程序翻译与程序解释
我们将人类语言变为计算机能看懂的语言,需要进行语言之间的转换。程序翻译就是将较为高级的计算机语言L1转为较为低级的计算机语言L0(编译器),L0就是计算机实际执行的语言。程序解释就是把较为高级的语言L1,作为用L0语言实现的一个程序的输入,然后得到较为低级计算机语言L0。
程序翻译与程序解释的对比:
- 计算机实际执行的指令都是L0
- 翻译过程生成新的L0程序,解释过程不生成新的L0程序
- 解释过程由L0编写解释器去执行L1程序
程序翻译的常见语言:C/C++, Object-C, Golang; 程序解释的常见语言:Python, Php, JavaScript。而Java和C#是属于翻译加解释性语言,Java程序转为JVM字节码的过程是程序翻译,由JVM字节码变成机器码的过程是程序解释。
计算机的层次
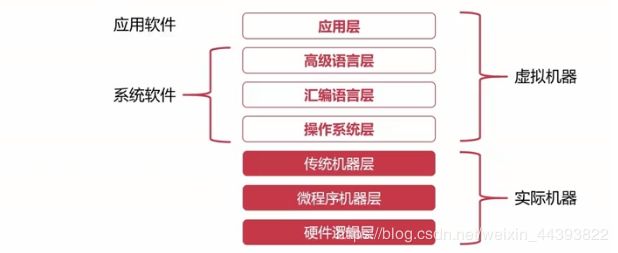
硬件逻辑层:门、触发器等逻辑电路组成,属于电子工程领域。
微程序机器层:编程语言是微指令集,微指令所组成的微程序直接交由硬件执行。
传统机器层:编程语言是CPU指令集(机器指令),编程语言和硬件直接相关,不同架构的CPU使用不同的指令集。一条机器指令对应一个微程序,一个微程序对应一组机器指令。
操作系统层:向上提供了简易的操作界面,向下对接了指令系统,管理硬件资源,操作系统层是硬件和软件之间的适配层。
汇编语言层:编程语言是汇编语言,汇编语言可以翻译成可直接执行的机器语言,完成翻译过程的程序就叫汇编器。
高级语言层:编程语言为广大程序员所接受的高级语言,高级语言的种类非常多,有几百种,常见的高级语言有C/C++、Java、Python、Golang等。
应用层:满足计算机针对某种用途而专门设计,例如常见的办公软件Excel,Word,PPT等。
计算机的字符与编码集
使用7个bits就可以完全表示ASCII码,包含95个可打印字符,33个不可打印字符(包括控制字符),即 33+95=128=27,但是这个ASCII码在很多应用和很多国家中的符号都无法表示,例如数学符号:“ ÷ \div ÷ ≠ \neq = ≥ \geq ≥ ≈ \approx ≈ π \pi π”。所以在第一次对ASCII码进行扩充时,7bits=> 8bits,在可拓展的ASCII码中,包含了常见的运算符,带音标的欧洲字符,和其他常用符、表格等。
字符编码集的国际化:由于欧洲、中亚、东亚、拉丁美洲国家的语言多样性,造成语言体系不一样,不以有限字符组合的语言,尤其是中国、韩国、日本的语言最为复杂。国标2312(GB2312):《信息交换用汉字编码字符集-基本集》是中文编码集,一共收录了7445个字符,包括6763个汉字和682个其他符号。Unicode(统一码、万国码、单一码)定义了世界通用的符号集,UTF-*实现了编码,UTF-8以字节为单位对Unicode进行编码。Unicode是兼容全球的字符集。
计算机的总线与IO设备
计算机的总线
什么是总线?
总线提供了对外的接口,不同设备可以通过USB(Universal Serial Bus)接口进行连接,连接的标准,促使外围设备接口的统一。

当我们的输入设备向计算机中输入信息,要求计算机给出指定输出时,这时需要IO总线来进行总线连接。
总线的分类?
- 片内总线:芯片内部的总线,寄存器与寄存器之间,寄存器与控制器、运算器之间。片内总线是高集成度芯片内部的信息传输线。
- 系统总线:CPU、主内存、IO设备、各组件之间的信息传输线
- 数据总线:双向传输各个部件的数据信息,数据总线的位数(总线宽度)是数据总线的重要参数,一般与CPU位数相同(32位、64位)
- 地址总线:指定源数据或目的数据在内存中的地址,地址总线的位数与存储单元有关。若地址总线位数=n,寻址范围:0~2n
- 控制总线:控制总线是用来发出各种控制信号的传输线,控制信号经由控制总线从一个组件发给另外一个组件,控制总线可以监视不同组件之间的状态(就绪/未就绪)
总线的仲裁:为了解决总线使用权的冲突问题
总线的仲裁方法:
- 链式查询:好处:电路复杂度低,仲裁方式简单;坏处:优先级低的设备难以获得总线的使用权,对电路故障敏感。
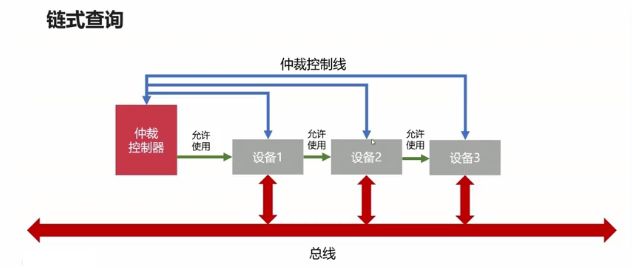
- 计时器定时查询

- 独立请求
- 每个设备均有总线独立连接仲裁器
- 设备可单独向仲裁器发送请求和接受请求
- 当同时收到多个请求信号,仲裁器有权按优先级分配使用权
- 好处:响应速度快,优先顺序可动态改变,设备连线多,总线控制复杂。
常见的IO设备
常见的输入设备:分为字符输入设备和图像输入设备。字符输入设备就如键盘,图像输入设备如鼠标、数位板、扫描仪等。

常见的输出设备:显示器、打印机、投影仪
输入输出接口的通用设计:我们需要考虑如何向设备发送数据?如何读取数据?该设备有没被占用?设备是否已经启动?设备是否已经连接?等等还有其他问题,基于对输入输出设备接口通用设计的考虑,至少应该有以下几部分:
- 数据线
- 是I/O设备与主机之间进行数据交换的传送线
- 单向传输数据线
- 双向传输数据线
- 状态线
- IO设备状态向主机报告的信号线
- 查询设备是否已经正常连接并就绪
- 查询设备是否已经被占用
- 命令线
- CPU向设备发送命令的信号线
- 发送读写信号
- 发送启动停止信号
- 设备选择线
- 主机选择I/O设备进行操作的信号线
- 对连在总线上的设备进行选择
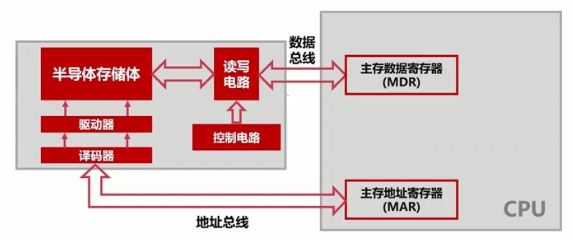
计算机的存储器
存储器的分类:
- 按存储介质分:
- 半导体存储器:例如内存、U盘、固态硬盘
- 磁存储器:例如磁带、磁盘等
- 按存取方式分类:
- 随机存储器(RAM):随机读取,与位置无关
- 串行存储器:与位置有关,按顺序查找
- 只读存储器(ROM):只读不写,BIOS就是存储在只读存储器中
存储器的层次:
对于存储器,我们希望它读写速度快,存储容量大,而价格最好低一些。存储器的层次结构如下图:
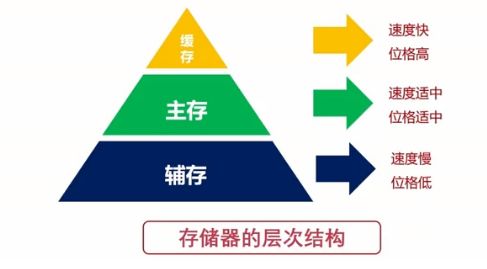
缓存:指的就是CPU中的寄存器以及高速缓存;主存:计算机中的内存;辅存:计算机的外部存储设备,比如磁盘、U盘、移动硬盘等。
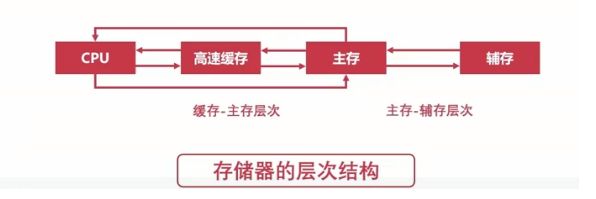
缓存-主存层次:
- 原理:局部性原理,局部性原理就是指CPU访问存储器时,无论是存取指令还是存取数据,所访问的存储单元都趋集于在一个较小的连续区域中。
- 实现:在CPU与主存之间增加一层速度快(容量小)的Cache
- 目的:解决主存速度不足的问题
主存-辅存层次:
- 原理:局部性原理
- 实现:主存之外增加辅助存储器(磁盘,SD卡,U盘等)
- 目的:解决主存容量不足的问题
计算机突然断电,内存数据就会丢失,但是计算机断电,磁盘数据不会丢失。
- 主存储器——内存
- 辅助存储器——磁盘
- 表面是可磁化的硬磁特性材料
- 移动磁头径向运动读取磁道信息
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AxmJKPih-1594280655311)(https://img2020.cnblogs.com/blog/1975191/202005/1975191-20200521170338917-1253978303.png)]
计算机的辅助存储器常用算法
- 先来先服务算法
- 最短寻道时间优先
- 与磁头当前位置有关
- 优先访问离磁头最近的磁道
- 扫描算法(电梯算法)
- 循环扫描算法
计算机的高速缓存
高速缓存的工作原理
字:是指存放在一个存储单元中的二进制代码组合
字块:存储在连续的存储单元中而被看作是一个单元的一组字节
一个字快有32位,一个字快共B个字,主存中共M个字块,则主存总字数=B*M,主存总容量(bits)=B*M*32。字的地址包含两部分:前m位指定字快的地址,后b位指定字在字快中的地址。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Wp6hNGsg-1594280655314)(https://img2020.cnblogs.com/blog/1975191/202005/1975191-20200522111951957-248737695.png)]
例子:假设主存用户空间容量位4G,字快大小为4M,字长为32位,则对于字地址中的快地址m和块内地址b的位数,至少应该是多少?
由于1G=1024M,所以4G=4096M,由于字快大小为4M,所以字快数为: 4096 ÷ 4 = 1024 4096\div4=1024 4096÷4=1024,所以字快地址m= log 2 1024 = 10 \log_2 1024=10 log21024=10,块内字数为 4 M ÷ 32 b i t = 1048576 b i t 4M\div32bit=1048576bit 4M÷32bit=1048576bit,块内地址b= log 2 1048576 = 20 \log_2 1048576=20 log21048576=20,所以快地址m的位数至少为10,块内地址b的位数最少为20。
我们已经知道在CPU与主存之间存在高速缓存,当CPU需要的数据在缓存里时,则CPU直接从高度缓存中读取数据即可,不需要去访问主存,但当CPU需要的数据不在缓存里时,则需要去主存拿。由于CPU的处理速度远远快于主存的读取速度和数据传输速度,所以这样会导致CPU空转来等待数据传输,造成资源上的浪费。所以我们尽可能的让CPU去高速缓存中读取数据,因此我们需要一个量化指标,这个量化指标就是命中率。命中率是衡量缓存的重要性能指标,理论上CPU每次都能从高速缓存中读取数据的时候,命中率为1。假设访问主存次数为 N m N_m Nm,访问Cache次数为: N c N_c Nc,则命中率h为: h = N c N c + N m h=\frac{N_c}{N_c+N_m} h=Nc+NmNc。现在来看看访问效率e,假设访问主存时间为 t m t_m tm,访问缓存时间为 t c t_c tc,则访问Cache-主存系统的平均时间为: t a = h t c + ( 1 − h ) t m t_a=ht_c+(1-h)t_m ta=htc+(1−h)tm,则访问效率e为: e = t c t a = t c h t c + ( 1 − h ) t m e=\frac{t_c}{t_a}=\frac{t_c}{ht_c+(1-h)t_m} e=tatc=htc+(1−h)tmtc
例子:假设CPU在执行某段程序时,共访问了Cache命中2000次,访问主存50次,已知Cache的存取时间为50ns,主存的存取时间为200ns,求Cache-主存系统中的命中率、访问效率和平均访问时间。
命中率: h = N c N c + N m = 2000 2000 + 50 = 0.97 h=\frac{N_c}{N_c+N_m}=\frac{2000}{2000+50}=0.97 h=Nc+NmNc=2000+502000=0.97
访问效率: e = t c t a = t c h t c + ( 1 − h ) t m = 50 0.97 ∗ 50 + ( 1 − 0.97 ) 200 = 0.917 = 91.7 % e=\frac{t_c}{t_a}=\frac{t_c}{ht_c+(1-h)t_m}=\frac{50}{0.97\ast50+(1-0.97)200}=0.917=91.7\% e=tatc=htc+(1−h)tmtc=0.97∗50+(1−0.97)20050=0.917=91.7%
平均访问时间: 0.97 ∗ 50 + ( 1 − 0.97 ) 200 = 54.5 n s 0.97\ast50+(1-0.97)200=54.5ns 0.97∗50+(1−0.97)200=54.5ns
高速缓存的替换策略
由于高速缓存的运行需要良好的缓存替换策略。什么是缓存替换策略呢?就是当高速缓存中没有数据时,需要从主存中载入所需要的数据。高速缓存中常见的替换策略:
- 随机算法
- 先进先出算法(FIFO)
- 最不经常使用算法(LFU)
- 优先淘汰最不经常使用的字快
- 需要额外的空间记录字快的使用频率
- 最近最少使用算法(LRU)
- 优先淘汰一段时间内没有使用的字快
- 有多种实现方法,一般使用双向链表
- 把当前访问节点置于链表前面(保证链表头部节点是经常使用的)
计算机的指令系统
- 机器指令的形式
机器指令主要有两部分组成:操作码、地址码。地址码直接给出操作数和操作数的地址,分三地址指令、二地址指令和一地址指令,最后还有零地址指令,零地址指令在机器指令中没有地址码,用来进行空操作、停机操作、中断返回操作等。

- 机器指令的操作类型:
- 数据传输:在寄存器之间、寄存器与存储单元、存储单元之间传送;还可以进行数据独写、交换地址数据、清零置一等操作。
- 算术逻辑操作:操作数之间的加减乘除运算;操作数的与或非等逻辑运算
- 移位操作:数据左移(乘2)、数据右移(除2);完成数据在算术逻辑单元的必要操作。
- 控制指令:主要有等待指令、停机指令、空操作指令、中断指令等。
- 机器指令的寻址方式
- 指令寻址:顺序寻址;跳跃寻址
- 数据寻址:
- 立即寻址:指令直接获得操作数,无需访问存储器
- 直接寻址:直接给出操作数在主存中的地址,寻找操作数简单,无需计算数据地址
- 间接寻址:指令地址码给出的是操作数地址的地址,需要访问一次或多次主存来获取操作数
| 寻址方式 | 优点 | 缺点 |
|---|---|---|
| 立即寻址 | 速度块 | 地址码位数限制操作数表示范围 |
| 直接寻址 | 寻找操作数简单 | 地址码位数限制操作数表示范围 |
| 间接寻址 | 操作数寻址范围大 | 速度较慢 |
计算机的控制器
控制器是协调和控制计算机运行的,计算机的控制器主要组成部分如下:
- 程序计数器:程序计数器用来存储下一条指令的地址;循环从程序计数器中拿出指令;当指令被拿出时,指向下一条指令
- 时序发生器:电气工程领域,用于发送时序脉冲;CPU根据不同的时序脉冲有节奏的进行工作
- 指令译码器:指令译码器是控制器主要部件之一,计算机指令由操作码和地址码组成,翻译操作码对应的操作以及控制传输地址码对应的数据
- 各种寄存器
- 指令寄存器:指令寄存器也是控制器的主要部件之一,从主存或高速缓存读取计算机指令
- 主存地址寄存器:保存当前CPU正要访问的内存单元的地址
- 主存数据寄存器:保存当前CPU正要读或写的内存数据
- 通用寄存器:用于暂时存放或传送数据和指令,可保存ALU的运算中间结果,容量比一般的专用寄存器要大
- 总线
计算机的运算器
运算器是用来进行数据加工运算的,主要组成部分如下:
- 数据缓冲器:分为输入缓冲和输出缓冲,输入缓冲暂时存放外设送过来的数据;输出缓冲暂时存放送往外设的数据
- ALU:算术逻辑单元,是运算器的主要组成,常见的位运算(左右移、与或非等),算数运算(加减乘除等)
- 通用寄存器
- 状态字寄存器:存放运算状态(条件码、进位、溢出、结果正负等);存放运算控制信息(调试跟踪标记位、允许中断位等)
- 总线
计算篇
进制概述
进制是一种计数方式,亦称为进位计数法或位值计数法,用有限种数字符号来表示无线的数值,使用的数字符号的数目称为这种进位制的基数或底数。例如n=10[0-9]称为十进制;还有例如玛雅文明的玛雅数字,因努伊特的因努伊特数字使用的就是二十进制;像时间、坐标、角度等量化数据使用的就是六十进制。但我们使用的计算机喜欢二进制,但是使用二进制表达太长了,使用大进制可以解决这个问题,计算机常用的大进制有八进制、十六进制。因为八进制和十六进制都满足2的n次方要求。例如1024分别使用二进制、八进制、十六进制表示为:1024 = 0b1000000000 = oO2000 = ox400
二进制的运算基础
1.整数十进制和二进制的互相转换
(整数)十进制转换二进制:重复相除法。例子:十进制数101转为二进制:如下
| 重复除以2 | 得商 | 取余数 |
|---|---|---|
| 101/2 | 50 | 1 |
| 50/2 | 25 | 0 |
| 25/2 | 12 | 1 |
| 12/2 | 6 | 0 |
| 6/2 | 3 | 0 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1 |
最后,倒着取余数,所以101的二进制表示是:1100101。二进制转为十进制使用的是按权展开法: 1100101 = 1 × 2 6 + 1 × 2 5 + 0 × 2 4 + 0 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 101 1100101 = 1 \times 2^6 + 1 \times 2^5 + 0 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 +0 \times 2^1 + 1 \times 2^0 = 101 1100101=1×26+1×25+0×24+0×23+1×22+0×21+1×20=101
再举一个例子:十进制数237转为二进制,如下
| 重复除以2 | 得商 | 取余数 |
|---|---|---|
| 237/2 | 118 | 1 |
| 118/2 | 59 | 0 |
| 59/2 | 29 | 1 |
| 29/2 | 14 | 1 |
| 14/2 | 7 | 0 |
| 7/2 | 3 | 1 |
| 3/2 | 1 | 1 |
| 1/2 | 0 | 1 |
最后倒着取数,所以237的二进制表示是:11101101。使用按权展开法把二进制转为十进制: 11101101 = 1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 0 × 2 4 + 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 237 11101101 = 1 \times 2^7 + 1 \times 2^6 + 1 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 +0 \times 2^1 + 1 \times 2^0 = 237 11101101=1×27+1×26+1×25+0×24+1×23+1×22+0×21+1×20=237
二进制转为十进制:按权展开法的的计算公式如下:
N = d n − 1 d n − 2 . . . d 1 d 0 = d n − 1 r n − 1 + d n − 2 r n − 2 + d 1 r + d 0 N = d_{n-1}d_{n-2}...d_1d_0 = d_{n-1}r^{n-1} + d_{n-2}r^{n-2} + d_1r +d_0 N=dn−1dn−2...d1d0=dn−1rn−1+dn−2rn−2+d1r+d0
2.小数十进制和二进制的互相转换
如果这个十进制是小数,则使用重复相乘法。例如 25 32 \frac{25}{32} 3225转为二进制,如下:
| 重复乘以2 | 得积 | 取整 |
|---|---|---|
| 25 32 × 2 \frac{25}{32} \times 2 3225×2 | 25 16 = 1 + 9 16 \frac{25}{16} = 1+\frac{9}{16} 1625=1+169 | 1 |
| 9 16 × 2 \frac{9}{16} \times 2 169×2 | 9 8 = 1 + 1 8 \frac{9}{8} = 1+\frac{1}{8} 89=1+81 | 1 |
| 1 8 × 2 \frac{1}{8} \times 2 81×2 | 1 4 = 0 + 1 4 \frac{1}{4} = 0+\frac{1}{4} 41=0+41 | 0 |
| 1 4 × 2 \frac{1}{4} \times 2 41×2 | 1 2 = 0 + 1 2 \frac{1}{2} = 0+\frac{1}{2} 21=0+21 | 0 |
| 1 2 × 2 \frac{1}{2} \times 2 21×2 | 1 = 1 + 0 1 = 1+0 1=1+0 | 1 |
最后顺着取整数: 25 32 \frac{25}{32} 3225的二进制表示为:0.11001。现在再使用按权展开法把二进制转为十进制数:
N = 0.11001 = 1 × 2 − 1 + 1 × 2 − 2 + 0 × 2 − 3 + 0 × 2 − 4 + 1 × 2 − 5 = 0.78125 = 25 32 N = 0.11001 = 1 \times 2^{-1} + 1 \times 2^{-2} + 0 \times 2^{-3} + 0 \times 2^{-4} + 1 \times 2^{-5} = 0.78125 = \frac{25}{32} N=0.11001=1×2−1+1×2−2+0×2−3+0×2−4+1×2−5=0.78125=3225
有符号数和无符号数
正的237使用二进制表示为:+237 = 011101101 ,负的237使用二进制表示为:-237 = 111101101,在计算机中,使用0表示正数,使用1表示负数。但计算机是怎么判断它是数字位还是符号位的呢?这就需要使用原码表示法了,在原码表示法中,使用0表示正数,使用1表示负数,规定符号位位于数值的第一位,表达简单明了,是我们最容易理解的表示法。0有两种表示法:00或10,在使用原码进行运算时,会非常复杂,特别是两个操作符号不同的时候,我们需要进行判断两个操作数得绝对值大小,使用绝对值大的数减去绝对值小的数,对于符号值,以绝对值大的为准。因此我们希望找不到不同符号操作数运算更加简单得方法,也就是可以使用正数来代替负数,使用加法操作来代替减法操作,从而消除减法。于是出现了二进制的补码表示法,补码的定义如下:
x = { x 2 n > x ≥ 0 2 n + 1 + x 0 > x ≥ − 2 n x = \begin{cases} x & 2^{n} > x \geq 0 \\ 2^{n+1} + x & 0 > x \geq -2^n \end{cases} x={x2n+1+x2n>x≥00>x≥−2n
例1:x=-13,计算x的二进制原码和补码
原码:x=1,1101
补码: 2 n + 1 + x = 2 4 + 1 − 13 = 100000 − 1101 = 10011 2^{n+1} + x = 2^{4+1} - 13 = 100000 - 1101 = 10011 2n+1+x=24+1−13=100000−1101=10011,这里的最高位1是符号位
补码:x = 1,0011
例2:x=-7,计算x的二进制原码和补码
原码:x=1,0111
补码: 2 n + 1 + x = 2 4 + 1 − 7 = 100000 − 0111 = 11001 2^{n+1} + x = 2^{4+1} - 7 = 100000 - 0111 = 1 1001 2n+1+x=24+1−7=100000−0111=11001,这里的最高位1是符号位
补码:x = 1,1001
例3:x=-1,计算x的二进制原码和补码
原码:x=1,0001
补码: 2 n + 1 + x = 2 4 + 1 − 1 = 100000 − 0001 = 11111 2^{n+1} + x = 2^{4+1} - 1 = 100000 - 0001 = 1 1111 2n+1+x=24+1−1=100000−0001=11111,这里的最高位1是符号位
补码:x = 1,1111
我们引入补码的初衷是由于减法运算复杂,希望找到使用正数代替负数的方法,使用加法代替减法操作,从而消除减法,但是通过上面例子可以看到,补码的引入,并没有实现校除减法的目的。于是就提出了反码,反码的目的是找出原码和补码之间的规律,消除转换过程中的减法,反码的定义如下:
x = { x 2 n > x ≥ 0 ( 2 n + 1 − 1 ) + x 0 > x ≥ − 2 n x = \begin{cases} x & 2^{n} > x \geq 0 \\ (2^{n+1} - 1) + x & 0 > x \geq -2^n \end{cases} x={x(2n+1−1)+x2n>x≥00>x≥−2n
例1:x=-13,计算x的二进制原码和反码
原码:x=1,1101
补码: ( 2 n + 1 − 1 ) + x = ( 2 4 + 1 − 1 ) − 13 = 011111 − 1101 = 10010 (2^{n+1} - 1) + x = (2^{4+1} -1) - 13 = 011111 - 1101 = 10010 (2n+1−1)+x=(24+1−1)−13=011111−1101=10010,这里的最高位1是符号位
补码:x = 1,0010
例2:x=-7,计算x的二进制原码和反码
原码:x=1,0111
补码: ( 2 n + 1 − 1 ) + x = ( 2 4 + 1 − 1 ) − 7 = 011111 − 0111 = 11000 (2^{n+1} - 1) + x = (2^{4+1} -1) - 7 = 011111 - 0111 = 11000 (2n+1−1)+x=(24+1−1)−7=011111−0111=11000,这里的最高位1是符号位
补码:x = 1,1000
我们可以根据反码补码的定义进行计算,找一找三者的关系:
| 十进制 | 原码 | 补码 | 反码 |
|---|---|---|---|
| 13 | 0,1101 | 0,1101 | 0,1101 |
| -13 | 1,1101 | 1,0011 | 1,0010 |
| -7 | 1,0111 | 1,1001 | 1,1000 |
| -1 | 1,0001 | 1,1111 | 1,1110 |
根据这个表格中数据,我们可以发现正数原码、补码、反码的值都是一样的;负数的反码等于原码除符号位外都按位取反,负数的补码等于反码+1。同样的,小数的二进制也满足这个规律,二进制小数的补码定义如下:
x = { x 1 > x ≥ 0 2 + x 0 > x ≥ − 1 x = \begin{cases} x & 1 > x \geq 0 \\ 2 + x & 0 > x \geq -1 \end{cases} x={x2+x1>x≥00>x≥−1
例1: x = 9 16 x=\frac{9}{16} x=169,计算x的二进制原码、反码和补码
原码:x=0,0.1001 反码:x=0,0.1001 补码:x=0,0.1001
例2: x = − 11 32 x=-\frac{11}{32} x=−3211,计算x的二进制原码、反码和补码
原码:x=1,0.01011 反码:x=1,1.10100 补码:x=1,1.10101
定点数与浮点数
定点数的表示方法:纯小数的小数点放在符号位与数值位之间,纯整数的小数点放在数值位末尾,我们的定点数的保存需要乘以比例因子。
定点数的纯小数表示:
| 数值 | 符号位 | 数值位 |
|---|---|---|
| 0.1011 | 0 | 1011 |
| -0.1011 | 1 | 1011 |
定点数的纯整数表示:
| 数值 | 符号位 | 数值位 |
|---|---|---|
| 1011 | 0 | 1011 |
| -1011 | 1 | 1011 |
由于计算机处理的很大程度上不是纯小数或纯整数,如果数据范围很大,定点数就难以表达。
浮点数的表示格式:使用科学计数法表示浮点数, 123450000000 = 1.2345 × 1 0 1 1 123450000000 = 1.2345 \times 10^11 123450000000=1.2345×1011,1.2345是尾数,10是基数,11是阶码。浮点数的表示格式为: N = S × r j N = S \times r^j N=S×rj,S代表尾数,r代表基数,j表示阶码,尾数规定使用纯小数。例子如下:
N = S × r j N = S \times r^j N=S×rj
11.0101 = 0.110101 × 2 1 0 11.0101 = 0.110101 \times 2^10 11.0101=0.110101×210,这里都是二进制表示,阶码10对应十进制数为2
11.0101 = 0.0110101 × 2 1 1 11.0101 = 0.0110101 \times 2^11 11.0101=0.0110101×211,这里都是二进制表示,阶码11对应十进制数为3
| 阶码符号位 | 阶码数值位 | 尾数符号位 | 尾数数值位(8位) |
|---|---|---|---|
| 0 | 10 | 0 | 11010100 |
| 0 | 11 | 0 | 01101010 |
浮点数的表示范围:假设阶码值取m位,尾数值取n位, N = S × r j N = S \times r^j N=S×rj,阶码能够表示的最大值为: 2 m − 1 2^m-1 2m−1,阶码表示范围为: [ − ( 2 m − 1 ) , 2 m − 1 ] [-(2^m-1),2^m-1] [−(2m−1),2m−1];尾数能够表示的最大值为: 1 − 2 − n 1 - 2^{-n} 1−2−n,尾数能够表示的最小值为: 2 − n 2^{-n} 2−n,尾数表示的范围为: [ − ( 1 − 2 − n ) , − 2 − n ] [-(1 - 2^{-n}),-2^{-n}] [−(1−2−n),−2−n] [ 2 − n , 1 − 2 − n ] [2^{-n},1-2^{-n}] [2−n,1−2−n]

单精度浮点数:使用4字节、32位来表示浮点数(float)
双精度浮点数:使用8字节、64位来表示浮点数(double)
浮点数的规格化:尾数规定使用纯小数,尾数最高位必须是1.
例1:设浮点数的长度为16位,阶码为5位,尾数为是11位,将十进制数 13 128 \frac{13}{128} 12813表示为二进制浮点数
由于正数的原码=反码=补码: x = 0.0001101000 x = 0.0001101000 x=0.0001101000,浮点数的规格化: x = 0.1101000 ∗ 2 − 11 x = 0.1101000 * 2^{-11} x=0.1101000∗2−11
| 阶码符号位 | 阶码数值位 | 尾数符号位 | 尾数数值位 |
|---|---|---|---|
| 1 | 0011 | 0 | 1101000000 |
例2:设浮点数的长度为16位,阶码为5位,尾数为是11位,将十进制数 − 54 -54 −54表示为二进制浮点数
原码: x = 1 , 110110 x = 1,110110 x=1,110110,浮点数的规格化: x = − 0.110110 ∗ 2 − 110 x = -0.110110 * 2^{-110} x=−0.110110∗2−110,由于尾数为110110 0000,则尾数反码为:001001 1111,尾数补码为:001010 0000
| 阶码符号位 | 阶码数值位 | 尾数符号位 | 尾数数值位 |
|---|---|---|---|
| 0 | 0110 | 1 | 001010 0000 |
定点数与浮点数的对比:
- 定点数与浮点数位数相同时,浮点数表示的范围更大
- 当浮点数尾数为规格化数时,浮点数的精度更高
- 浮点数运算包含阶码和位数,浮点数的运算更为复杂
总结:浮点数在数的表示范围、精度、溢出处理、编程等方面均优于定点数;浮点数在数的运算规则、运算速度、硬件成本等方面不如定点数。
定点数的加减法运算
整数加法:A[补] + B[补] = [A+B][补](mod 2 n + 1 2^{n+1} 2n+1)
小数加法:A[补] + B[补] = [A+B][补](mod2)
注意:定点数的加减法运算,数值位与符号位一同运算,并将符号位产生的进位自然丢掉
例1:A=-110010,B=001101,求A+B
A[补] = 1,001110,B[补] = B[原] = 0,001101,A[补] + B[补] = (A+B)[补] = 1,011011,则A + B = -100101
例2:A=-0.1010010,B=0.0110100,求A+B
A[补] = 1,1.0101110,B[补] = B[原] = 0.0110100,A[补] + B[补] = (A+B)[补] = 1,1.1100010,则A + B = -0.0011110
例3:A=-10010000,B=-11010000,求A+B
A[补] = 1,01110000,B[补] = 1,00110000,A[补] + B[补] = (A+B)[补] = 0,10100000,则A + B = 10100000,将结果转为十进制表示是160。我们可以把A和B转为十进制进行运算:A=-144,B=-208,A+B=-352,我们会发现二进制的计算结果是错误的。这是由于我们在计算时,对符号位的进位自然丢掉了,这是就发生了溢出,那我们如何来判断溢出呢?双符号位判断法:单符号位表示变成双符号位:0=>00,1=>11,双符号位产生的进位丢弃,结果的双符号位不同则表示溢出。
整数减法:A[补] - B[补] = A + (-B)[补](mod 2 n + 1 2^{n+1} 2n+1)
小数减法:A[补] - B[补] = A + (-B)[补](mod2)
-B[补]等于B[补]连同符号位按位取反,末位加一
浮点数的加减法运算
运算过程:对阶->尾数求和->尾数规格化->舍入->溢出判断
x = 0.1101 × 2 01 x = 0.1101 \times 2^{01} x=0.1101×201
y = ( − 0.1010 ) × s 11 y = (-0.1010) \times s^{11} y=(−0.1010)×s11
对阶:浮点数尾数运算简单,浮点数位数实际小数位与阶码有关,阶码按小阶看齐大阶的原则。对阶的目的是使得两个浮点数阶码一致,使得尾数可以进行运算
| 阶码符号位 | 阶码数值位 | 尾数符号位 | 尾数数值位 |
|---|---|---|---|
| 00 | 0001 | 00 | 1101 |
| 00 | 0011 | 11 | 1010 |
对阶后:
x = 0.001101 × 2 11 x = 0.001101 \times 2^{11} x=0.001101×211
y = ( − 0.1010 ) × s 11 y = (-0.1010) \times s^{11} y=(−0.1010)×s11
| 阶码符号位 | 阶码数值位 | 尾数符号位 | 尾数数值位 |
|---|---|---|---|
| 00 | 0011 | 00 | 0011(01) |
| 00 | 0011 | 11 | 1010 |
舍去01,在进行尾数求和,x[原]=00.0011,x[补]=00.0011,y[原]=11.1010,y[补]=11.0110,S=(x+y)[补]=11.1001
| 阶码符号位 | 阶码数值位 | 尾数符号位 | 尾数数值位 |
|---|---|---|---|
| 00 | 0011 | 11 | 1001 |
尾数规格化:对补码进行规格化需要判断两种情况:S>0和S<0,S[补] = 00.1xxxxxxx(S>0),S[补] = 11.0xxxxxxx(S<0),符号位与最高位不一致,如果不满足此格式,则需要进行左移,同时阶码相应变化,以满足规格变化。
| 阶码符号位 | 阶码数值位 | 尾数符号位 | 尾数数值位 |
|---|---|---|---|
| 00 | 0011 | 11 | 1001 |
S = (x + y)[补] = 11.1001 = 11.(1)0010(左移)
| 阶码符号位 | 阶码数值位 | 尾数符号位 | 尾数数值位 |
|---|---|---|---|
| 00 | 0010 | 11 | 0010 |
S=(x+y)[补]=11.0010 (x+y)[原]=-0.1110 x + y = − 0.1110 × 2 10 x+y=-0.1110\times2^{10} x+y=−0.1110×210
尾数规格化一般情况下都是左移,双符号位不一致得情况下需要右移(定点运算得溢出情况),右移的话需要进行舍入操作,舍入就是指“0舍1入”法(二进制得四舍五入),S[补]=10.10110111,由于双符号位不一致,所以需要进行右移操作,S[补] = 11.010110111,同时阶码需要加1。对于定点数运算来说,双符号位不一致为溢出,对于浮点数运算来说,浮点数尾数双符号位不一致不算溢出,因为尾数符号可以进行右规,浮点数运算主要通过阶码得双符号位判断是否溢出,如果规格化后,阶码双符号位不一致,则认为是溢出。