原文地址:https://zhuanlan.zhihu.com/p/146543473
前言
大家好,我是潜心。由于在小组会上提到了“过拟合”现象,发现自己很难给它下一个标准且规范的定义。因此查了一些资料,并简单做了下实验,进行简单整理。 本文约,预计阅读15分钟。
过拟合与欠拟合
以一个简单的线性回归开始
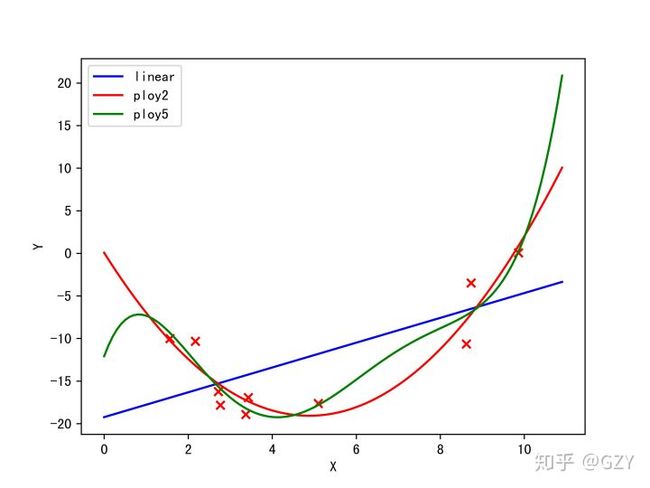
简单的线性回归能够直观的反应过拟合和欠拟合的现象。首先我们随机生成若干个符合某二次多项式函数的点,并加入噪声,作为训练集。然后我们使用三个简单的线性模型(1次项回归,2次多项式回归、5次多项式回归)【注:多次项回归本质来说还是一个线性模型】来进行拟合,最后可视化,如下图所示。
我们发现,1次项的模型结构简单,但拟合结果其他二者更差,无法捕捉数据中的规律,所以该模型出现了欠拟合的现象。
5次多项式回归的全部特征为:(此处我们在最简单的线性回归中只使用了1个特征和1个偏置,故5次包含共6个特征),我们发现该模型的结构相对复杂,所以在图中拟合训练集的情况甚至比二次模型更好。
若我们重新生成一些点,区间为,当作测试集,我们依旧做图观察之前训练得到的三个模型对测试集的拟合程度。【由于5次项模型在-2以后拟合过差,导致图被拉长,可视化效果不好,所以不显示-2以后的情况】
如上图所示,我们发现5次项模型已经完全偏离了测试数据点的轨迹,比1次模型的拟合结果更差,而2次模型还是能够较好的拟合。这个结果说明5次模型结构过于复杂,以致于无法良好地拟合其他数据的结果,出现了过拟合的现象。
统计学中过拟合与欠拟合的定义
在统计学中,过拟合(overfitting)是指相较有限的数据而言,模型参数过多或者结构过于复杂,且过于紧密或精确地匹配特定数据集,以致于无法良好地拟合其他数据或预测未来的观察结果的现象。
与过拟合相对应的欠拟合(underfitting)是指相较于数据而言,模型参数过少或者模型结构过于简单,以至于无法捕捉到数据中的规律的现象。
过拟合的原因
之所以存在过拟合的可能,是因为选择模型的标准和评价模型的标准是不一致的。举例来说,选择模型时往往是选取在训练数据上表现最好的模型;但评价模型时则是观察模型在训练过程中不可见数据上的表现。
过拟合尤其容易在训练迭代次数相对有限训练样本过多的时候。此时,模型会拟合训练数据中特征的随机噪声,而这些与目标函数之间并无因果关系。在这种过拟合的过程中,模型在训练样本上的效果会持续提升,但在训练中不可见的数据(通常是验证集)上的效果会变得更差。
故对上述进行总结就是:当模型尝试“记住”训练数据而非从训练数据中学习规律时,就可能发生过拟合。
过拟合的本质
过拟合的本质是训练算法从统计噪声中不自觉获取了信息并表达在了模型结构的参数当中。相较用于训练的数据总量来说,一个模型只要结构足够复杂或参数足够多,就总是可以完美地适应数据的【理想情况】。
违反奥卡姆剃刀原则
奥卡姆剃刀原则:
“奥卡姆剃刀”是一种常用的、自然科学研究中最基本的原则,即“若有多个假设与观察一致,则选择最简单的那个”。(其实关于奥卡姆剃刀的讨论非常复杂,并且也有其数学公式---所罗门的归纳推理理论,这里我们只是最为简单的描述)
在机器学习中,模型的典型产出过程是由机器学习算法在训练集上进行训练,希望得到的模型能够在训练过程中不可见的验证集上表现良好。而当引入相较数据集而言过多的参数时,或使用相较数据集而言过于复杂的模型时,则就出现了过拟合现象,违反了上说所说的奥卡姆剃刀原则。
Bias-Variance-Tradeoff
在机器学习中,人们总是希望自己的训练的模型能够准确的描述数据背后的规律。但我们会遇到三种误差来源:随机误差,偏差和方差。而我们在讨论模型的过拟合和欠拟合现象时,总是离不开偏差和方差。
数学定义
随机误差:随机误差是数据本身的噪音带来的,这种误差是不可避免的。一般认为随机误差服从均值为0的高斯分布,记作。若为标签,为特征变量,那么数据背后的真实规律可以描述为:
偏差:偏差是指模型的预期(或平均)预测与预测的正确值之间的差【假设可以多次重复整个模型构建过程,产生的模型将有一系列的预测】。我们记为的估计模型,因此偏差可以表示为:
方差:在概率论和统计学中,一个随机变量的方差描述的是它的离散程度,也就是该变量离其期望值的距离。通俗来讲,方差指模型通过学习拟合出来的结果的不稳定性【同样,假设多次重复整个模型构建过程】。方差可以表示为:
图表示
我们可以使用靶心图创建偏差和方差的图形可视化。假设目标的中心是一个完美地预测正确值的模型。随着远离靶心,预测会越来越糟。想象一下,我们可以重复整个模型构建过程,以获得对目标的多次单独命中。根据上述定义,偏差与方差的变化图如下所示:
左上图是理想情况下,点都分布在靶心位置,即偏差和方差都很小。右上图点都分布在靶心的周围,因此偏差较小,但这些点较于分散,则方差较大。左下图点分布集中,说明方差较小,但距离靶心远,所以偏差较大。右下是最坏的情况,点全部分散在靶的外围,且不集中,故偏差和方差都大。
过拟合与Bias-Variance
真实值和预测值的平方,即 均方误差(MSE) 可以表示为:
该误差可以分解为:
故均方误差的大小由偏差的平方、方差和随机误差决定。因此以模型的复杂度为横坐标,误差为纵坐标,绘制曲线图[2]:
由此可见,模型的总体误差随着模型的复杂度的上升先下降后上升,偏差一直下降,在经过最优点后,下降趋势变缓;方差缓慢上升,但经过最优点后,大幅度上升。模型复杂度较低时【偏差大、方差小】,可以认为是一种欠拟合现象,模型复杂度较高时【偏差小、方差大】,可以认为是一种过拟合现象。而最优点【偏差小、方差小】是一种理想情况,因此我们需要合理的权衡偏差和方差的关系,找到尽可能优的模型结构。
然而在现实环境中,有时候我们很难计算模型的偏差与方差。因此,我们需要通过外在表现,判断模型的拟合状态,如下图所示[3]:
通过上图发现:
- 训练集误差和交叉验证集误差近似时且较大时:偏差大/欠拟合
- 交叉验证集误差远大于训练集误差时:方差大/过拟合
处理欠拟合与过拟合
欠拟合
当模型处于欠拟合状态时,根本的办法是增加模型复杂度。我们一般有以下一些办法:
- 增加模型的迭代次数;
- 更换描述能力更强的模型;
- 生成更多特征供训练使用;
- 降低正则化水平。
过拟合
当模型处于过拟合状态时,根本的办法是降低模型复杂度。我们则有以下一些武器:
- 扩增训练集;
- 减少训练使用的特征的数量;
- 提高正则化水平。
总结
1、人们可以在直觉上理解过拟合:“过去的经验可被分为两个部分:与将来有关的数据、与将来无关的数据(噪声)”。在其他条件都相同的情况下,预测的难度越大(不确定性越高),则过去信息中需要被当做噪声忽略的部分就越多。问题的难点在于,如何确定哪些数据应当被忽略,即我们该如何去找到一个最优的模型复杂度,其实就是偏差与方差的权衡。
2、一般来说,当参数的自由度或模型结构的复杂度超过数据所包含信息内容时,拟合后的模型可能使用任意多的参数,这会降低或破坏模型泛化的能力。
3、发生过拟合时,模型的偏差小而方差大。过拟合一般可以视为违反奥卡姆剃刀原则。发生欠拟合时,模型的偏差大而方差小。
参考文献
[1]. 维基百科-过拟合
[2]. http://scott.fortmann-roe.com/docs/BiasVariance.html
[3]. https://www.learnopencv.com/bias-variance-tradeoff-in-machine-learning/
[4]. https://liam.page/2017/03/25/bi