复杂网络实验2:WS小世界模型(matlab)
复杂网络实验2:WS小世界模型(matlab)
一.思路
1.小世界模型3个参数,N为点的数目,K表示每个点左边K/2个邻居,右边K/2个邻居,一共K个邻居,P代表每条边以多少概率重连
2.首先给定这三个参数(源码是人工输入,解析代码是我在代码中直接给出,通过修改代码中3个参数实现模型的变化)
3.画出以圆为轮廓的N个点
4.给出邻接矩阵A,将初始图像(每个点和邻居有边)的边存放在这里(先不画出来,就存在矩阵里,到时候边改过后再画)
5.修改边(其实是修改邻接矩阵)
6.按照邻接矩阵画出最后的图像
二.代码+解析
N=100 //给定100个点
K=4 //左右各两个邻居,一共4个邻居
p=0.1 //每条边以0.1的概率重连
这一块给定了模型的初始的3参数
angle=0:2*pi/N:2*pi-2*pi/N; //1:狗:2的意思是,以狗为间隔,返回1和2之间的数组成的数组
//这里右边一部分不能取2*pi,不然就取了N+1个数,因为区间两边都算在内
//如果你右边取2*pi,我们是围成一个圆,这个2*pi的点其实就是0这个点
//这里只是取了100个角度,分摊2*pi这个圆
x=100*cos(angle); //X取半径为100,角度为angle的圆上点的横坐标,注意这是个数组
y=100*sin(angle);
plot(x,y,'ro','MarkerEdgeColor','g','MarkerFaceColor','r','MarkerSize',8) //画出这100个点
//‘ro’在绘图时,只画红色的圈,xi和yi的交点
//‘g’点的边缘取绿色
//‘r’点的内部取红色
//‘8’标记大小为8
hold on; //图像保持住,画出点,等等还要画线
到这里把点画好了
A=zeros(N); //生成一个N行N列的0矩阵赋值给A,当做初始化的邻接矩阵
for i=1:N
for j=i+1:i+k/2 //每次取当前点,并且问候右边两个邻居,给他们握手(互相加1)
jj=j; //j赋值给jj
if j>N
jj=mod(j,N); //如果j的右边邻居超过N,要从0开始找他的邻居
end
A(i,jj)=1;
A(jj,i)=1; //邻接矩阵表现成我和这个邻居各加1,其实是个对称矩阵,在操作右上角的时候顺带操作左下角
end
end
//为什么要把j给jj? jj是处理过的j,因为j有时候会超过N,要转一圈
//这个时候我们的基础图完成了,接下来开始随机重连
//把图存放在邻接矩阵A中
for i=1:N
for j=i+1:i+k/2 //还是和上面一样我每次找到右边的邻居
jj=j;
if j>N
jj=mod(j,N); //如果j可能是假邻居的话,那么jj必定是真的邻居
end
p1=rand(1,1); //生成一个1行1列的数赋值给p1
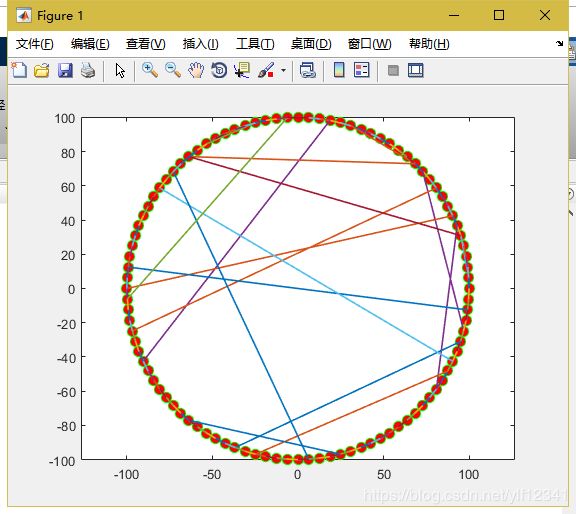
if p1 A(i,jj)=0; A(jj,i)=0; A(i,i)=inf; //怕等等自己和自己连,取值无穷 a=find(A(i,:)==0); //找到A中i行所有等于0的,就是没和i相连的点,a数组存放着所有和当前点没有连接的点 rand_data=randi([1,length(a)],1,1); //1行1列,随机数,随机找一列 jjj=a(rand_data); A(i,jjj)=1; A(jjj,i)=1; A(i,i)=0; //从inf恢复 end end end for i=1:N for j=i+1:N //遍历邻接矩阵的右上角 if A(i,j)~=0 //如果点i与点j之间有边(邻接矩阵中A(i,j)为1) plot([x(i),x(j)],[y[i],y[j]],'linewidth',1.2); //在(x(i),y(i)),(x(j),y(j))之前生成边,线宽1.2 hold on; end end end axis equal; // 使横轴,纵轴相等 hold off; 生成的小世界图像如下图所示 三.源码
N=input('请输入最近邻耦合网络中节点的总数N:');
K=input('请输入最近邻耦合网络中每个节点的邻居数K:');
if K>floor(N-1)|mod(K,2)~=0;
disp('参数输入错误:K值必须是小于网络节点总数且为偶数的整数');
return ;
end
angle=0:2*pi./N:2*pi-2*pi/N;
angle=0:2*pi/N:2*pi-2*pi/N;
x=100*sin(angle);
y=100*cos(angle);
plot(x,y,'ro','MarkerEdgeColor','g','MarkerFaceColor','r','MarkerSize',8);
hold on;
A=zeros(N);
for i=1:N
for j=i+1:i+K/2
jj=j;
if j>N
jj=mod(j,N);
end
A(i,jj)=1;
A(jj,i)=1;
end
end
%WS小世界网络的代码
p=input('请输入随机化重连的概率p:');
for i=1:N
for j=i+1:i+K/2
jj=j;
if j>N
jj=mod(j,N);
end
p1=rand(1,1);
if p1四.小结