Morris二叉树遍历算法

在遍历儿叉树时，常常使用的是递归遍历，或者是借助于栈来迭代，在遍历过程中，每个节点仅访问一次，所以这样遍历的时间复杂度为O(n)，空间复杂度为O(n)，并且递归的算法易于理解和实现，二叉树的递归遍历算法代码如下：

儿叉树的定义：

typedef struct BNode {
    char ch;
    struct BNode *left, *right;
} BNode, *BiTree;

先序遍历：

/**
 * 递归先序遍历
 */
void preOrder_traverse_recur(BiTree T) {
    if(T == NULL) {
        return;
    } else {
        printf("%4c", T->ch);
        preOrder_traverse_recur(T->left);
        preOrder_traverse_recur(T->right);
    }
}

中序遍历：

/**
 * 递归中序遍历
 */
void inOrder_traverse_recur(BiTree T) {
    if(T == NULL) {
        return;
    } else {
        inOrder_traverse_recur(T->left);
        printf("%4c", T->ch);
        inOrder_traverse_recur(T->right);
    }
}

后序遍历：

/**
 * 递归后序遍历
 */
void postOrder_traverse_recur(BiTree T) {
    if(T == NULL) {
        return;
    } else {
        postOrder_traverse_recur(T->left);
        postOrder_traverse_recur(T->right);
        printf("%4c", T->ch);
    }
}

从上面的3中遍历方式可以看出，在遍历过程中，除了输出节点信息的语句位置不同以外，其他代码都是相同的。但是递归遍历过程的空间复杂度却是O(n)，就算是转换为使用栈空间迭代时间，还是没有改变算法对额外空间的需求，在学习数据结构课程时，还学习了线索二叉树，在线索二叉树中，使用线索来保存节点的前驱和后继的信息，而这些线索是利用了叶节点的空指针域来保存，所以知道了树种每个节点的前驱和后继的位置（指针）可以有效降低遍历过程中对空间的需求，但是使用线索二叉树必须先通过一次二叉树遍历算法，为二叉树建立线索，此外还需要标记每个节点的指针域是线索还是指针，比较复杂。下面来看看Morris二叉树遍历算法。

Morris算法与递归和使用栈空间遍历的思想不同，它使用二叉树中的叶节点的right指针来保存后面将要访问的节点的信息，当这个right指针使用完成之后，再将它置为NULL，但是在访问过程中有些节点会访问两次，所以与递归的空间换时间的思路不同，Morris则是使用时间换空间的思想，先来看看Morris中序遍历二叉树的算法实现：

/**
 *morris中序遍历二叉树
 */
void morris_inorder(BiTree T) {
    BNode *p, *temp;
    p = T;
    while(p) {
        if(p->left == NULL) {
            printf("%4c", p->ch);
            p = p->right;
        } else {
            temp = p->left;
            //找到左子树的最右子节点
            while(temp->right != NULL && temp->right != p) {
                temp = temp->right; 
            }
            if(temp->right == NULL) {
                temp->right = p;
                p = p->left;
            } else {
                printf("%4c", p->ch);
                temp->right = NULL;
                p = p->right;
            }
        }
    }
}

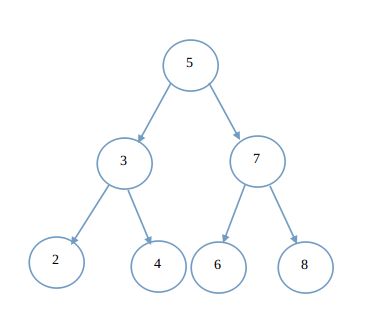
中序遍历的顺序是左-中-右，即先访问左子树，再访问根节点，最后访问右子树，在上面的算法进行遍历过程中，对于某个节点N，如果其左子树为空，那么就说明没有左子树，可以将这种情况视为左子树已经访问完毕，那么这个时候就访问根节点，再将当前节点指针指向根节点的右子树的根节点，进而访问右子树。如果根节点的的左子树不为空，那么就找到遍历左子树时访问的最后一个节点M(节点M的right指针一定为NULL)，将这个节点的right指针指向根节点，这样在访问完了根节点的左子树后，就可以根据这个right指针，来访问下面将要访问的节点，按照这个思路，画一个二叉树来说明：

在上图的二叉树中，如果使用Morris中序遍历方法，首先从根节点5开始，由于5的左子树不为空，那么找到5的左子树中，中序遍历过程中最后访问的那个节点，即5的左子树中的最右节点，这里是节点4，然后让节点4的右指针指向根节点5，再让当前指针指向5的左子树根节点，依次继续执行，直到执行访问到节点2，由于2的左子树为空，那么输出节点2的信息，此时2的右指针指向节点3，那么当前指针就指向节点3，然后节点3再次试图访问其左子树的根节点（节点2），由于2的右指针已经指向了3，所以就将3节点的信息输出，然后再访问3节点的右子树。访问过程中，以3-->2这条边为例，第一次经过这条边是找节点3的左子树的最右节点时，找到节点2的右子树不为空，第二次经过这条边是遍历完了节点3的左子树，然后消除节点3的左子树最右节点的右指针的过程，所以整个过程中，这条边访问了两次，由此可见，遍历过程中，每条边最多访问了两次，而n个节点的二叉树有n-1条边，所以遍历整个二叉树的时间复杂度为O(n)，并且遍历过程中使用了一个临时指针，所以空间复杂读为O(1)。

与二叉树的递归遍历相比较，Morris遍历方法，每条边访问两次，比递归遍历过程访问次数多，虽然空间复杂度降低了，但是遍历的时间增加了，不过递归遍历也会有函数调用的开销。

与Morris中序遍历相似，Morris先序遍历的代码如下：

void morris_preOrder(BiTree T) {
    BNode *p = T, *temp;
    while(p != NULL) {
        if(p->left == NULL) {
            printf("%4c",p->ch);
            p = p->right;
        } else {
            temp = p->left;
            while(temp->right != NULL && temp->right != p) {
                temp = temp->right;
            }
            if(temp->right == NULL) {
                printf("%4c", p->ch);
                temp->right = p;
                p = p->left;
            } else {
                temp->right = NULL;
                p = p->right;
            }
        }
    }    
}

与中序遍历相比较，先序遍历将输出当前节点放在了第一次到达左子树最右节点时。这与二叉树先序遍历的思想相符合，在Morris先序遍历过程中，当到达节点的左子树最右节点时，输出根节点，然后当前指针指向根节点的左子树，即先访问根节点，再访问左子树。利用左子树的最右指针来方便得到根节点的右子树的根节点。

Morris后序遍历二叉树的算法与上面的算法思想一致，只是在遍历前，增加了一个类似头节点的节点作为整个遍历过程的起始节点。由于后序遍历先访问左子树，然后是右子树，最后访问根节点，所以在Morris算法遍历过程中，增加一个头节点dump表示新二叉树的根节点，让这个新的根节点的左指针指向原二叉树的根节点，右指针为NULL。对于某个节点N，先遍历N的左子树的左子树，再逆序遍历从N节点的左子树的根节点到中序遍历过程访问的最右节点这条路径上的节点，以上面的二叉树的节点5为例，节点5的左子树的根节点为3，那么先遍历3的左子树，再逆序遍历从节点3到节点4这条路径上面的节点，所谓逆序，就是根据指针关系，原本先要访问节点3，然后再访问节点4，那么逆序遍历就是先访问节点4，再访问节点3，起始这个逆序遍历过程就是逆序遍历单链表的过程。

Morris后序遍历的代码如下：

/**
 * morris后序遍历算法 
 */
void morris_postOrder(BiTree T) {
    BNode *dump = malloc(sizeof(BNode));
    BNode *p, *temp;
    dump->left = T;
    p = dump;
    while(p) {
        if(p->left == NULL) {
            p = p->right;
        } else {
            temp = p->left;
            while(temp->right != NULL && temp->right != p) {
                temp = temp->right;
            }
            if(temp->right == NULL) {
                temp->right = p;
                p = p->left;
            } else {
                printReverse(p->left, temp);
                temp->right = NULL;
                p = p->right;
            }
        }
    }
    free(dump);
}

代码中的printReverse()函数就是逆序遍历从p->left到temp这条路径上的节点的过程，其代码如下：

/**
 * 相当于单链表的反转
 */
void reverse(BNode *from, BNode *to) {
    BNode *x, *y, *z;
    if(from == to) {
        return;
    }
    x = from;
    y = from->right;
    while(x != to) {
        z = y->right;
        y->right = x;
        x = y;
        y = z;
    }
}

void printReverse(BNode *from , BNode *to) {
    BNode *p;
    reverse(from, to);
    p = to;
    while(1) {
        printf("%4c", p->ch);
        if(p == from) {
            break;
        }
        p = p->right;
    }
    reverse(to, from);
}

printReverse函数先将从from节点到to节点的这条路径反转，再输出，最后还原。

总结

Morris遍历算法充分利用了叶子节点的空指针域，遍历过程，先利用空指针保存以后要到达的路径，这个指针使用完成之后再恢复。整个遍历过程都是按照二叉树递归遍历的思路进行，代码大体上相似，只是在输出节点信息（即访问节点信息）处有不同。Morris以时间换空间，对路径进行了重复的访问，达到了空间复杂度为O(1)的效果。

Reference

http://www.cnblogs.com/AnnieKim/archive/2013/06/15/MorrisTraversal.html

http://blog.sina.com.cn/s/blog_65dcacbb0100hwba.html