快速排序全面讲解(含复杂度证明)——即将引出八大排序算法
全面解析快速排序(包括证明)
1.快速排序简介:
好看的图:
快速排序是目前公认的平均状态下速度最快的一种排序算法
优点如下:
1.原地排序:空间复杂度为O(1),相对于归并排序来说,占用非常小的内存便可以实现很高效的排序的效果
2.平均状态下的时间复杂度始终未O(logN),属于非常高效的排序算法(下面会给出证明)
缺点如下:
快速排序是不稳定的排序,因为牵扯到空间地址的跳跃交换,所以快速排序不能够保证在出现相同的元素的情况下的稳定的排序效果
2.快速排序的时间复杂度分析:
在参考了中国大神的笔记之后,对快排这类递归式 的分支算法的复杂度的分析有了如下几个认识:
1.任意一个递归式的算法的复杂度很大程度上要考虑到递归树的深度(快排的递归的深度我之后会援引大神的图片来解释)
2.任意一个算法的市价复杂度Log(k,n),不管k的大小,只要k是属于常数级别的我们都可以将其考虑成log(2,n)的复杂度也就是O(
logN)的复杂度,这一点我们应用的是高中的对数的换底公式,正因为这一点,快速排序的划分只要是常数倍数的,不管是1:99,1:999,1:9999,只要不是1:(n-1) ,那么在考虑到数据足够大的情况下,我们的时间复杂度还是O(logN),所以说,平均状态下,快排效果最好
3.对于快速排序,我们需要记住一点,复杂度是完全体现在画风的平衡性上的,划分的越均衡(二叉递归树越趋近于满二叉树),那么二叉树的深度就越浅,当然我们递归的深度就会越小,时间复杂度就会越低,排序的效果就会越好,(1:9的递归树表示如下图所示)
4.快速排序的最优复杂度证明:(常数倍数的都可以通过类似的方式导出)
T(n)=2T(n/2)+f(n)----f(n)-O(n),因为实际上我们对每一层递归树进行划分的时候,都是将整个数组都遍历了一遍
T(n)=4T(n/4)+2f(n)
...log2N=k,共进行k次
T(n)=nT(1)+kf(n)=O(n)+kO(n)==kO(n)=O(n*logn)
但是当我们每次划分的比例都是1:n-1,即最坏的情况的话
T(n)=T(1)+T(n-1)+f(n)=nT(1)+(n-1)f(n)=O(n*n)3.算法讲解:
1.引入算法到轮的伪代码:(看不懂?下面有详解)
QUICKSORT(A, p, r)//快速排序算法
if (p < r )
{
q = PARTITION(A, p, r)//分成左右两半,一半不大于A[r], 一半不小于A[r]
QUICKSORT(A, p, q-1)//递归左半
QUICKSORT(A, q+1, r) //递归右半
}
PARTITION(A, p, r)
x = A[r]//选择最后一个元素作为比较元素
i = p – 1//这个慢速移动下标必须设定为比最小下表p小1,否则两个元素的序列比如2,1无法交换
for j = p to r-1//遍历每个元素
{
if (A[j] <= x)//比较
{
i = i + 1//移动慢速下标
Exchange A[i] with A[j ]//交换
}
}
Exchange A[i+1] with A[r]//交换
return i + 1//返回分割点
在这里我对上面的核心部分,即partion函数给出自己用的一点帮助理解的想法思路:
首先我们可能最难看懂的就是i和j的关系,我们 可以这么来考虑
在j不断向前进的过程中,i之前的元素都是比划分点小的,i——j之间的元素都是比i大的,j之后的元素都是未知的,是需要我们之后去遍历来看的
那么首先i要比左界要少1的想法思路在于这一点:
因为我们可以通过伪代码发现,每次i出的元素都是比划分点小的集合的最右端,下一次我们和适合的j号元素进行交换的话,我们必须要先将i前进一格再进行交换,但是一开始,我们只能通过让i比左界小1的方式来通用化这种具体的实现操作
之后我们会发现要必须交换一次i+1和划分点(右界),这是为什么呢:
因为我们要保证划分点左侧都比划分点小,右侧比划分点大,那么i+1实际上是属于右侧的,我们将其交换位置是合情合理的事情,也是必须要做的事情
之后的就是返回这个划分点的位置然后分段递归的操作了
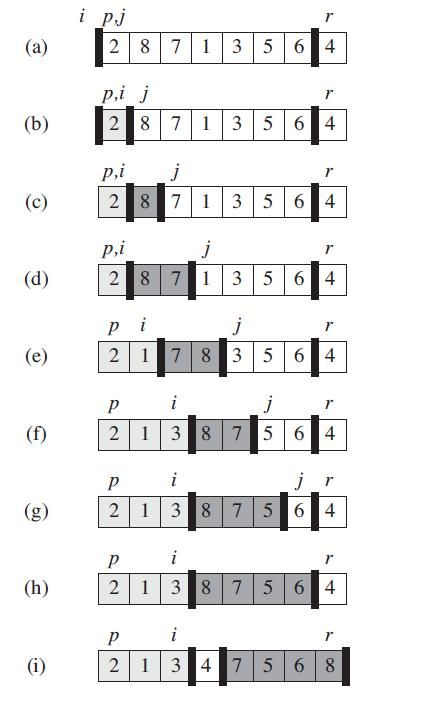
例题图片详解:
4.C++代码封装实现:(牵扯到友元函数的模板的一个问题)
1.算法导论中的实现
#include"iostream"
#include"cstdio"
#include"cstring"
#include"cstdlib"
#define N 100
using namespace std;
template class Qsort;
template
ostream& operator<<(ostream&,Qsort&);
template
istream& operator>>(istream&,Qsort&);
template //算法导论的版本
class Qsort
{
public:
Qsort()
{
memset(data,0,sizeof(data));
num=0;
}
friend ostream& operator<<<>(ostream&,Qsort&);
friend istream& operator>><>(istream&,Qsort&);
int partion(int,int);
void sort(int,int);
void presort()
{
sort(1,num);
}
void swap(int i,int j)
{
T t=data[j];
data[j]=data[i];
data[i]=t;
}
private:
T data[N];
int num;
};
template
ostream& operator<<(ostream& out,Qsort& k)
{
cout<<"Qsort结果如下:"<
istream& operator>>(istream& in,Qsort& k)
{
cout<<"please input the number of your data!"<>k.num;
for(int i=1;i<=k.num;i++) cin>>k.data[i];
return in; //为了实现流的连续输入
}
template
int Qsort::partion(int left,int right)
{
T key=data[right];
int i=left-1;
int j=left;
for(;j
void Qsort::sort(int left,int right)
{
if(left>=right) return ;
int q=partion(left,right);
sort(left,q-1);
sort(q+1,right);
}
int main()
{
Qsort my1;
Qsort my2;
cin>>my1>>my2;
my1.presort();
my2.presort();
cout<
关于上面的模板类的友元函数的问题:(在代码讨论区中有如下有效的解答)
//---test.h
#ifndef test_h_
#define test_h_
#include
using namespace std;
// 改动一:增加函数模板的声明——而这又需要先声明类模板
template class Test;
template
void display(Test &t);
template
class Test
{
private:
T x;
public:
Test (T x_): x(x_) {}
friend void display<>(Test &t);
// 改动二:在函数名后面加上<>,指明它是之前声明的函数模板 的实例
};
template
void display(Test &t)
{
cout << t.x << endl;
}
#endif // test_h_ 2.参考的另一种好实现的简约化代码实现
(只付上核心代码段)原理记住上面的会实现会写会理解就好,这个当做模板来记吧
void quicksort(int left,int right)
{
if(left>right) return ;
else
{
int i=left;
int j=right;
T t;
T temp=data[left];
while(i!=j)
{
while(i=temp) j--; //记住必须先动j
while(i 5.拓展阅读:快排的优化(随机化快排)
随机化快排解释
6.参考文献:
参考博客1(强烈推荐)
参考博客2(必看)
参考博客3(选看)